VCI - 18: 物理仿真 (Physics-Based Simulation)

Created on November 14, 2025

2025   ·   notes   VCI   physics-simulation   rigid-body   cloth-simulation   fluid-simulation   ·   VCI

课程: 北京大学视觉计算 (Visual Computing) 2025秋季 章节: 第18章 物理仿真 内容: 刚体动力学、布料仿真、流体仿真、粒子系统、软体仿真

目录

  1. 物理仿真概述
  2. 刚体动力学
  3. 粒子系统
  4. 布料仿真
  5. 软体仿真
  6. 流体仿真
  7. 碰撞检测与处理
  8. 求解器与积分方法
  9. 总结

1. 物理仿真概述

1.1 什么是物理仿真

物理仿真是使用物理和数学模型，在计算机中模拟真实世界物体的运动和变形。

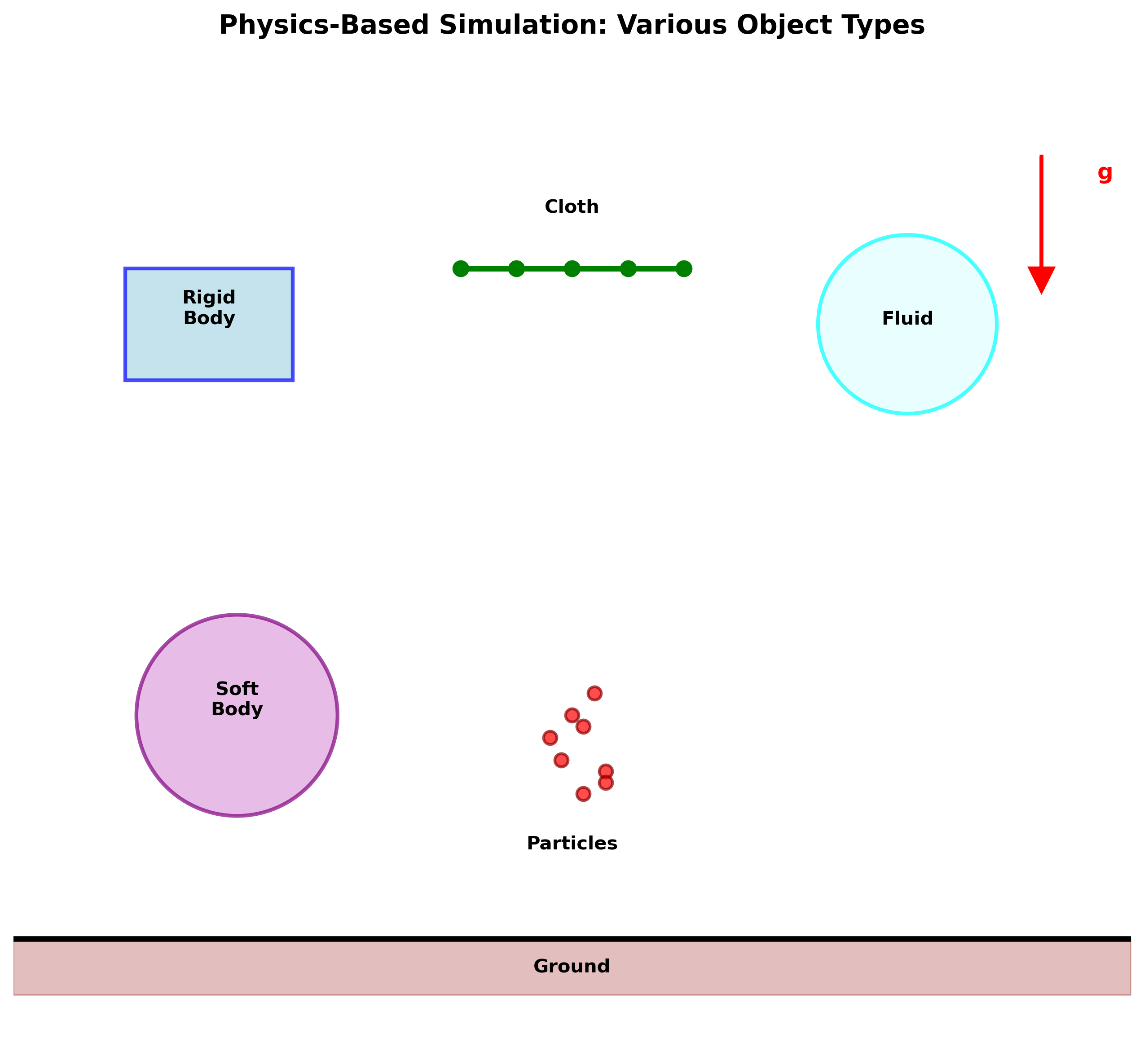
1.2 仿真的基本流程

Initialize State (x, v, a)
  ↓
for each time step:
  1. 计算力（重力、空气阻力、碰撞力等）
  2. 根据牛顿第二定律计算加速度：a = F/m
  3. 积分更新速度：v += a * Δt
  4. 积分更新位置：x += v * Δt
  5. 碰撞检测与响应
  6. 更新几何（用于渲染）

1.3 模拟分类

对象类型 特点 应用
刚体 形状不变，只有位移和旋转 场景物体、碎片
布料 网格结构，易弯曲，抗拉伸 衣物、旗帜、帐篷
软体 连续体，易变形，抗拉伸 果实、橡皮、肌肉
流体 连续体，无固定形状，易流动 水、烟、气体
粒子 点质量，易管理，性能好 火、灰尘、爆炸

2. 刚体动力学

2.1 牛顿运动定律

第一定律：物体保持匀速直线运动或静止，除非受力 \(\frac{d\mathbf{v}}{dt} = 0, \quad \text{if } \mathbf{F} = 0\)

第二定律：力等于质量乘以加速度 \(\mathbf{F} = m\mathbf{a} = m\frac{d\mathbf{v}}{dt}\)

第三定律：作用力与反作用力大小相等、方向相反 \(\mathbf{F}_{AB} = -\mathbf{F}_{BA}\)

2.2 刚体状态与运动

状态量：

  • 位置：\(\mathbf{x}(t)\)
  • 速度：\(\mathbf{v}(t) = \frac{d\mathbf{x}}{dt}\)
  • 加速度：\(\mathbf{a}(t) = \frac{d\mathbf{v}}{dt}\)
  • 旋转角速度：\(\boldsymbol{\omega}(t)\)

力与扭矩：

  • 合力：\(\mathbf{F} = \sum \mathbf{F}_i\)
  • 扭矩：\(\boldsymbol{\tau} = \mathbf{r} \times \mathbf{F}\)

运动方程： \(\mathbf{F} = m\mathbf{a}\) \(\boldsymbol{\tau} = \mathbf{I}\frac{d\boldsymbol{\omega}}{dt}\)

其中 \(\mathbf{I}\) 是惯性张量。

2.3 常见力

重力： \(\mathbf{F}_g = m\mathbf{g}, \quad \mathbf{g} = (0, -9.8, 0) \text{ m/s}^2\)

空气阻力： \(\mathbf{F}_{drag} = -c \mathbf{v}\)

弹簧力（Hooke定律）： \(\mathbf{F}_{spring} = -k(\|\mathbf{x}_1 - \mathbf{x}_2\| - L_0) \frac{\mathbf{x}_1 - \mathbf{x}_2}{\|\mathbf{x}_1 - \mathbf{x}_2\|}\)

3. 粒子系统

3.1 粒子系统的定义

粒子系统由大量简单粒子组成，每个粒子：

  • 位置：\(\mathbf{x}_i\)
  • 速度：\(\mathbf{v}_i\)
  • 质量：\(m_i\)
  • 其他属性：颜色、生命周期、纹理坐标等

3.2 粒子更新

力的计算： \(\mathbf{F}_i = m_i\mathbf{g} + \mathbf{F}_{external} + \mathbf{F}_{collision}\)

速度积分： \(\mathbf{v}_i^{t+\Delta t} = \mathbf{v}_i^t + \frac{\mathbf{F}_i}{m_i}\Delta t\)

位置积分： \(\mathbf{x}_i^{t+\Delta t} = \mathbf{x}_i^t + \mathbf{v}_i^{t+\Delta t}\Delta t\)

3.3 应用场景

  • 火焰和烟雾：每个粒子代表一团烟或火
  • 水花和液滴：液体飞溅的飞沫
  • 爆炸效果：碎片四散
  • 灰尘和雨：环境效果

4. 布料仿真

4.1 布料建模

布料表示为三角形网格，通过以下约束连接：

距离约束： 相邻顶点之间距离保持常数 \(\|\mathbf{x}_i - \mathbf{x}_j\|^2 = L_{ij}^2\)

弯曲约束： 相邻三角形之间的夹角保持常数（可选）

4.2 力与能量

弹性势能： \(E = \frac{1}{2}\sum_{edges} k(\|\mathbf{x}_i - \mathbf{x}_j\| - L_0)^2\)

重力： \(\mathbf{F}_g = m\mathbf{g}\)

阻尼： \(\mathbf{F}_{damp} = -c(\mathbf{v}_i - \mathbf{v}_j)\)

4.3 约束求解

Verlet 积分： 常用于布料仿真，避免显式速度计算 \(\mathbf{x}_{i}^{t+\Delta t} = 2\mathbf{x}_i^t - \mathbf{x}_i^{t-\Delta t} + \mathbf{a}_i(\Delta t)^2\)

约束投影： 迭代投影满足距离约束 \(\mathbf{x}_i' = \mathbf{x}_i + \frac{\Delta\|\mathbf{x}_i - \mathbf{x}_j\|}{2}(\mathbf{x}_i - \mathbf{x}_j)\)

5. 软体仿真

5.1 软体表示

网格：四面体网格或三角形表面网格

力：

  • 重力
  • 内部弹性力（通过应力-应变关系）
  • 约束力（保证体积不变）

5.2 有限元方法（FEM）

使用 FEM 计算应变和应力：

应变： \(\mathbf{E} = \frac{1}{2}(\mathbf{F}^T\mathbf{F} - \mathbf{I})\)

其中 \(\mathbf{F} = \nabla\phi\) 是变形梯度

应力： \(\mathbf{P} = \frac{\partial W}{\partial \mathbf{F}}\)

其中 \(W\) 是应变能密度

6. 流体仿真

6.1 Navier-Stokes 方程

动量方程： \(\rho(\frac{\partial \mathbf{u}}{\partial t} + \mathbf{u} \cdot \nabla\mathbf{u}) = -\nabla p + \mu\nabla^2\mathbf{u} + \mathbf{f}\)

连续方程（质量守恒）： \(\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho\mathbf{u}) = 0\)

对于不可压缩流体：\(\nabla \cdot \mathbf{u} = 0\)

6.2 求解方法

网格法：

  • MAC 网格：交错网格，速度在面上，压力在中心
  • 投影法：
    1. 计算临时速度（忽略压力）
    2. 求解压力泊松方程
    3. 投影速度到无散场

粒子法：

  • SPH（光滑粒子流体动力学）
  • FLIP/PIC（粒子浓度转移方法）

6.3 应用

  • 液体模拟：水、油、熔岩
  • 烟雾模拟：烟、雾、气体扩散
  • 气体效果：爆炸、风

7. 碰撞检测与处理

7.1 碰撞检测

广义阶段（Broad Phase）： 使用包围体（AABB、球体、OBB）快速排除不可能碰撞的对

窄义阶段（Narrow Phase）： 精确计算碰撞几何

  • 点-三角形
  • 边-边
  • 三角形-三角形

7.2 碰撞响应

碰撞约束： \((\mathbf{v}_1 - \mathbf{v}_2) \cdot \mathbf{n} \leq 0\)

冲量（Impulse）： \(\mathbf{j} = -\frac{(1+e)(\mathbf{v}_1 - \mathbf{v}_2) \cdot \mathbf{n}}{1/m_1 + 1/m_2}\)

其中 \(e\) 是恢复系数（0 = 完全非弹性，1 = 完全弹性）

速度更新： \(\mathbf{v}_1' = \mathbf{v}_1 + \frac{\mathbf{j}}{m_1}\mathbf{n}\) \(\mathbf{v}_2' = \mathbf{v}_2 - \frac{\mathbf{j}}{m_2}\mathbf{n}\)

8. 求解器与积分方法

8.1 显式积分（Explicit Integration）

欧拉法： \(\mathbf{v}^{t+\Delta t} = \mathbf{v}^t + \mathbf{a}^t\Delta t\) \(\mathbf{x}^{t+\Delta t} = \mathbf{x}^t + \mathbf{v}^t\Delta t\)

  • 优点：快速、易实现
  • 缺点：时间步长限制（\(\Delta t < \Delta t_{crit}\)），易数值不稳定

RK4（四阶 Runge-Kutta）：

  • 优点：更精确、更稳定
  • 缺点：计算成本高

8.2 隐式积分（Implicit Integration）

后向欧拉法： \(\mathbf{v}^{t+\Delta t} = \mathbf{v}^t + \mathbf{a}^{t+\Delta t}\Delta t\) \(\mathbf{x}^{t+\Delta t} = \mathbf{x}^t + \mathbf{v}^{t+\Delta t}\Delta t\)

  • 优点：无条件稳定，允许大时间步
  • 缺点：需解线性系统，计算成本高

8.3 约束求解

直接法：拉格朗日乘数法 迭代法：约束投影、Gauss-Seidel

9. 总结

9.1 仿真流程总结

  1. 初始化：设定初始位置、速度、材料参数
  2. 力计算：重力、外力、内力、约束力
  3. 数值积分：更新速度和位置
  4. 碰撞处理：检测并响应碰撞
  5. 约束满足：确保所有约束都被满足
  6. 几何更新：更新用于渲染的几何

9.2 实际应用

  • 电影和动画：角色动画、破坏效果、灾难场景
  • 游戏：实时物理引擎（PhysX、Bullet）
  • VR/AR：沉浸式体验中的真实感
  • 医学：手术模拟、组织模型
  • 工业：流体流动、结构分析

9.3 挑战与前景

当前挑战：

  • 实时求解大规模系统
  • 精度与性能的平衡
  • 多物体交互的复杂性

研究方向：

  • 神经网络加速仿真
  • 海量粒子系统
  • 多物理耦合（流体-固体、热-力学）
  • 逆向仿真（从动画反推物理参数）


Enjoy Reading This Article?

Here are some more articles you might like to read next:

  • notes of ML
  • notes of VCI
  • notes of AIP
  • notes of AI Math Fundamentals
  • notes of ICS