VCI - 17: 全局光照II - 路径追踪 (Global Illumination II - Path Tracing)

课程: 北京大学视觉计算 (Visual Computing) 2025秋季章节: 第17章全局光照II - 路径追踪内容: 路径追踪、蒙特卡洛积分、渲染方程、光路传输

1. Whitted光线追踪的局限

1.1 无法处理的现象

Whitted风格的光线追踪仅处理镜面反射和折射，无法表现：

漫反射表面的交互
- 无法模拟粗糙表面
- 只有精确镜面才能追踪反射
焦散效应（Caustics）
- 玻璃杯底部的光斑

需要光路：\(L[S\mid D]^{*}DE\)（多次镜面反射后到达漫反射面）
Whitted无法处理

颜色扩散（Color Bleeding）
- 漫反射物体相互照亮
- 需要光路：\(L[S\mid D]^+DE\)（多次漫反射后到达眼睛）
- Whitted无法处理

1.2 问题的本质

Whitted的核心限制：

仅追踪反射镜面 → 折射镜面
漫反射处停止追踪，不再递归
结果：无法表现多次漫反射的间接光照

解决方案：

在漫反射表面也发出光线
随机采样漫反射方向
这导向路径追踪（Path Tracing）

2. 光路传输记法

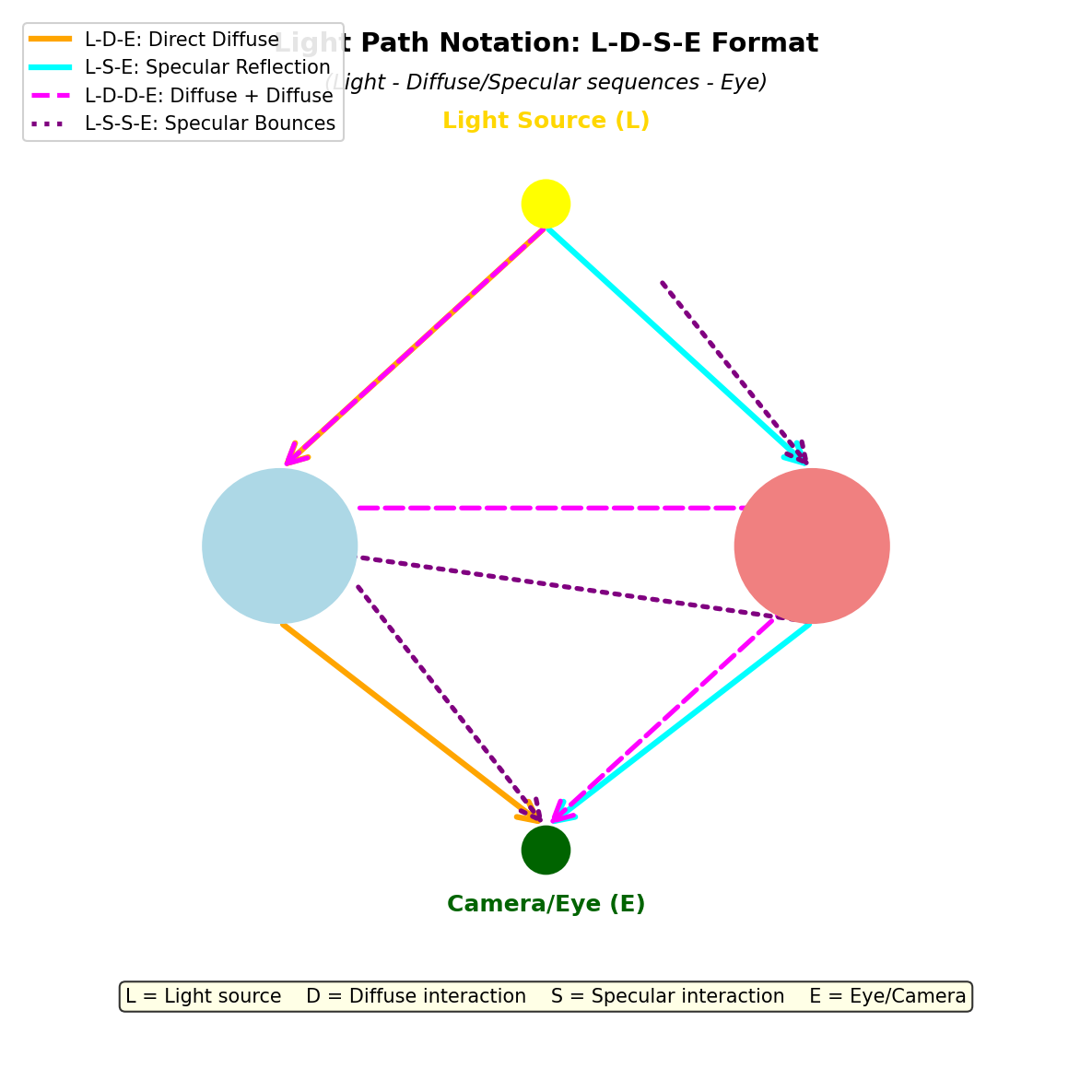
2.1 光路记号

L（Light）：光源发出的光
D（Diffuse）：漫反射
S（Specular）：镜面反射/折射
E（Eye）：进入相机
V（Volumetric）：体积散射（可选）

2.2 常见光路类型

光路	说明
LE	直接看到光源
LDE	直接光照（光→漫反射→眼睛）
LSE	镜面反射（光→镜面→眼睛）
LDDE	间接光照（光→漫反射→漫反射→眼睛）
LSE…DE	焦散：多次镜面后到漫反射
*L(S\|D)DE**	色彩扩散：多次漫反射

3. 辐射度量学基础

3.1 基本量

辐射能量（Radiant Energy） \(Q\)

单位：焦耳（J）
光携带的能量

辐射通量（Radiant Flux） \(\Phi = \frac{dQ}{dt}\)

单位：瓦特（W）或流明（lm）
单位时间内的能量

辐射强度（Radiant Intensity） \(I(\omega) = \frac{d\Phi}{d\omega}\)

单位：瓦特/立体角（W/sr）
单位立体角内的通量

辐照度（Irradiance） \(E = \frac{d\Phi}{dA}\)

单位：瓦特/平方米（W/m²）
单位面积接收的通量

亮度（Radiance） \(L(\theta, \phi) = \frac{d^2\Phi}{dA \cos\theta \, d\omega}\)

单位：瓦特/(平方米·立体角) (W/m²·sr)
最重要的量：光线追踪中直接计算的量

4. 渲染方程

4.1 反射方程

在点 \(\mathbf{x}\) 处，出射辐度等于自身发光加上来自各方向的入射光反射：

\[L_o(\mathbf{x}, \omega_o) = L_e(\mathbf{x}, \omega_o) + \int_{\Omega^+} f_r(\mathbf{x}, \omega_i, \omega_o) L_i(\mathbf{x}, \omega_i) (\omega_i \cdot \mathbf{n}) \, d\omega_i\]

其中：

\(L_o\)：出射辐度
\(L_e\)：自发光辐度
\(f_r\)：双向反射分布函数（BRDF）
\(L_i\)：入射辐度
\(\omega_i \cdot \mathbf{n}\)：入射角的余弦

4.2 全局照明方程

结合所有光源和反射，渲染方程为：

\[L_o(\mathbf{x}, \omega_o) = L_e(\mathbf{x}, \omega_o) + \int_{\Omega^+} f_r(\mathbf{x}, \omega_i, \omega_o) L_o(\mathbf{x}', -\omega_i) (\omega_i \cdot \mathbf{n}) \, d\omega_i\]

这个方程无解析解，需要数值求解。

5. 蒙特卡洛积分

5.1 基本思想

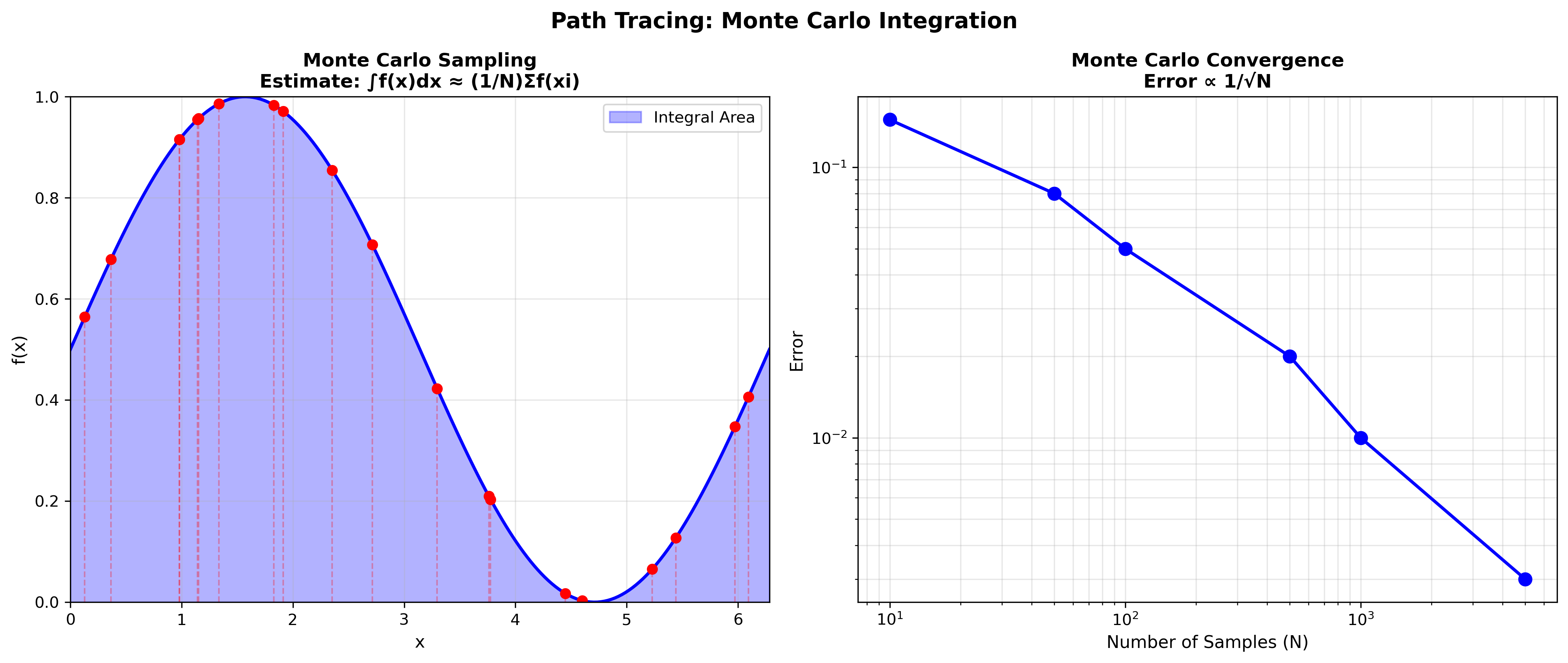
估计定积分： \(\int_a^b f(x) dx \approx \frac{b-a}{N} \sum_{i=1}^{N} f(x_i), \quad x_i \sim \text{Uniform}[a,b]\)

收敛性：

误差 \(\propto \frac{1}{\sqrt{N}}\)
需要 4 倍样本才能减少一半误差

5.2 半球积分应用

对反射方程的积分应用蒙特卡洛：

\[L_o = L_e + \int_{\Omega^+} f_r L_i \cos\theta \, d\omega\]

随机采样估计： \(L_o \approx L_e + \frac{1}{N} \sum_{i=1}^{N} \frac{f_r(\omega_i) L_i(\omega_i) \cos\theta_i}{p(\omega_i)}\)

其中 \(p(\omega_i)\) 是采样方向的概率密度函数。

6. 路径追踪算法

6.1 基本算法

PathTrace(ray, depth):
  if depth > MAX_DEPTH:
    return BLACK

  hit = ClosestIntersection(ray)
  if no hit:
    return BACKGROUND

  radiance = GetEmission(hit)  // 自发光

  // 随机采样下一个方向
  next_direction = SampleBRDF(hit, BRDF)
  next_ray = Ray(hit.point, next_direction)

  // 递归追踪
  incoming = PathTrace(next_ray, depth + 1)

  // 应用反射率并衰减
  reflection_coeff = BRDF(hit, next_direction)
  radiance += reflection_coeff * incoming

  return radiance

6.2 关键特点

在所有交点处采样：包括漫反射表面
随机方向：使用概率分布采样下一个方向
自动衰减：每次反射乘以 BRDF 系数
蒙特卡洛估计：多条光线平均得到结果

7. 重要性采样

7.1 方差减少

直接随机采样会产生高噪声。使用 重要性采样 减少方差：

\[\int f(x) dx = \int \frac{f(x)}{p(x)} p(x) dx \approx \frac{1}{N} \sum_{i=1}^{N} \frac{f(x_i)}{p(x_i)}, \quad x_i \sim p\]

最优选择：\(p(x) \propto f(x)\)

7.2 在路径追踪中的应用

对于 BRDF 积分，选择概率分布应与 BRDF 相关： \(p(\omega) \propto f_r(\omega) \cos\theta\)

常见策略：

漫反射：\(p(\omega) \propto \cos\theta\)（余弦加权）
镜面反射：\(p(\omega)\) 集中在反射方向附近

8. 进阶路径追踪

8.1 双向路径追踪（Bidirectional Path Tracing）

从光源和相机两端各生成路径，然后连接：

优点：处理焦散效应更好
缺点：实现复杂

8.2 Metropolis Light Transport (MLT)

使用 MCMC（马尔可夫链蒙特卡洛）方法追踪路径：

优点：自适应采样，对困难场景有效
缺点：实现复杂，收敛需要时间

8.3 分层采样（Stratified Sampling）

将采样空间分为多个子区间，在每个子区间采样：

优点：减少采样重复，降低方差
例：超采样，每像素 4×4 分层采样

9. 总结

9.1 路径追踪 vs Whitted追踪

特性	Whitted	路径追踪
镜面反射/折射	✓	✓
漫反射表面	✗	✓
焦散效应	✗	✓
颜色扩散	✗	✓
噪声	少	多（需降噪）
计算速度	快	慢
物理准确性	有限	高

9.2 路径追踪的意义

物理基础：基于光的物理性质和渲染方程
全局光照：自然处理所有间接光照
渲染框架：现代离线渲染的标准方法
实时应用：现代 GPU 加速使其逐渐实用

9.3 降噪技术

路径追踪的高噪声是其主要缺点，常用降噪技术：

更多采样：最直接但昂贵
分层采样：减少采样重复
重要性采样：聚焦采样到高贡献区域
滤波：渲染后应用降噪滤波
深度学习：神经网络降噪（NVIDIA DLSS 等）