VCI - 16: 全局光照I - Whitted光线追踪 (Global Illumination I - Ray Tracing)
课程: 北京大学视觉计算 (Visual Computing) 2025秋季 章节: 第16章 全局光照I - Whitted光线追踪 内容: 光线投射、递归光线追踪、光线-表面相交、加速结构、抗锯齿
目录
1. 光线追踪概述
1.1 为什么需要光线追踪
光栅化 (Rasterization) 的局限性:
- 仅支持直接照明(光从光源出发,最多反弹一次,进入眼睛)
- 难以处理阴影(需要额外的阴影贴图技术)
- 不支持透明和半透明材质
- 难以模拟多次光反弹(全局光照)
- 点光源假设(面光源需要复杂积分)
光线追踪 (Ray Tracing) 的优势:
- 自然处理反射、折射、透射
- 自动计算阴影(包括软阴影)
- 支持多次光线反弹和全局光照
- 支持面光源
- 在物理上更加可靠
1.2 光线追踪的基本思想
光线追踪通过向后追踪光线 (backward ray tracing) 来计算像素颜色:
- 从相机眼睛出发,穿过每个像素投射光线进入场景
- 找到光线与场景的最近交点
- 在交点处进行着色,计算直接光照
- 递归地追踪反射和折射光线
- 所有光线贡献之和即为该像素的最终颜色
2. 光线投射(Ray Casting)
2.1 光线投射的定义
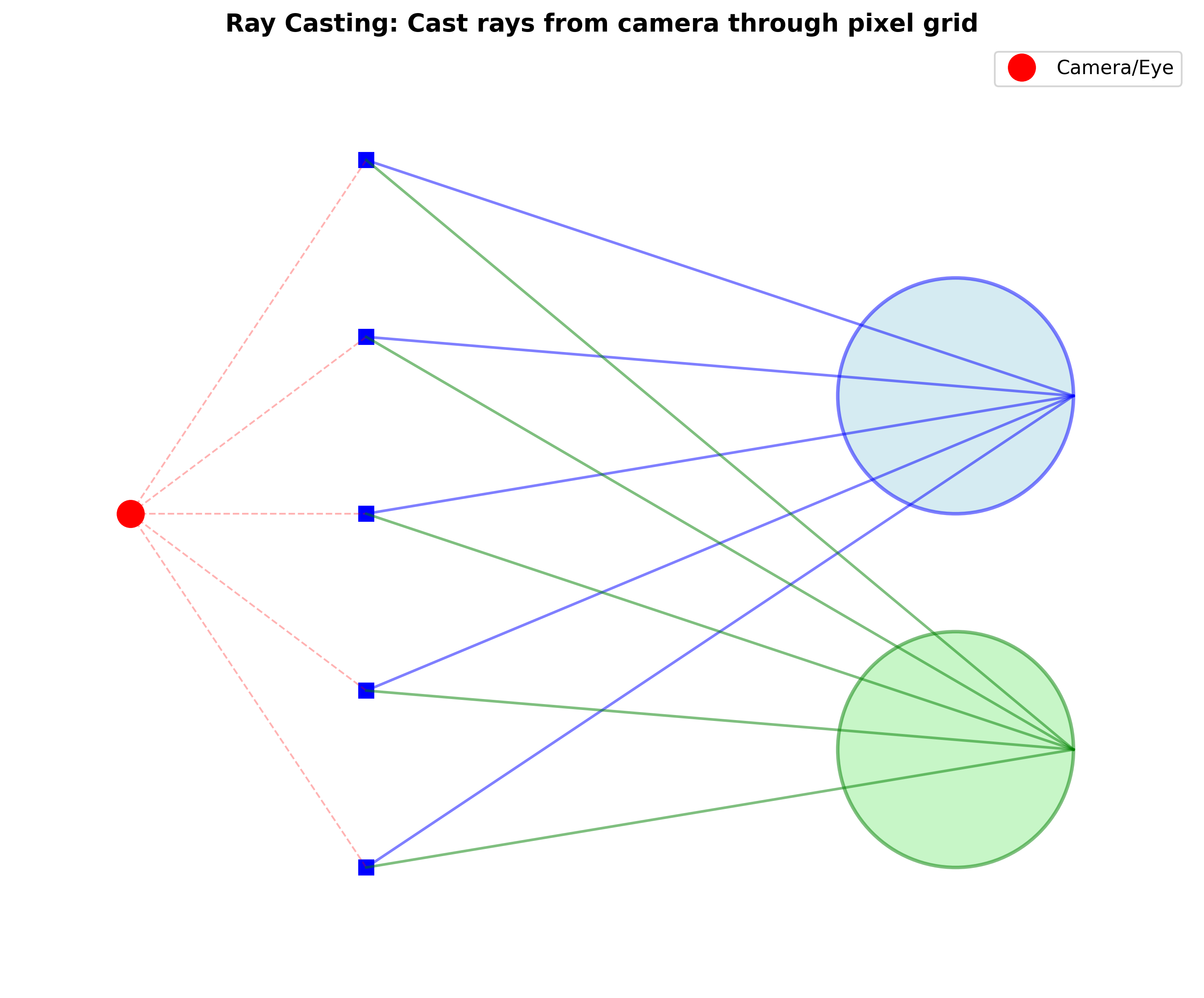
光线投射 (Ray Casting) 是光线追踪的基础,是一种灵活的可见性算法。
基本步骤:
- 对每个像素 \((x, y)\)
- 从相机眼睛出发,通过该像素投射一条光线进入场景
- 找到光线与所有表面的交点,获取最近的交点
- 在该交点处进行着色计算,得到像素颜色
2.2 光线投射伪代码
Raycast()
{
for each pixel (x, y) {
color(pixel) = Trace(ray_through_pixel(x, y))
}
}
Trace(ray)
{
// 发射光线,返回沿光线反向传播的RGB辐度
object_point = Closest_intersection(ray)
if object_point exists:
return Shade(object_point, ray)
else:
return Background_Color
}
Shade(point, ray)
{
// 返回离开该点的光线辐度
normal = compute_surface_normal(point)
radiance = 0
for each light source {
shadow_ray = create_ray(point, light)
if !in_shadow(shadow_ray) {
radiance += phong_illumination(point, light)
}
}
return radiance
}
2.3 光线投射的特点
- 灵活性高:易于处理各种表面类型和材质
- 支持透明:可以自然处理半透明物体(光栅化难以实现)
- 着色准确:基于几何和光照的物理基础
3. 光线-表面交点计算
3.1 光线方程
一条光线可表示为参数方程:
\[\mathbf{r}(t) = \mathbf{p} + t\mathbf{d}\]其中:
- \(\mathbf{p}\):光线起点(origin)
- \(\mathbf{d}\):光线方向(direction),通常为单位向量 \(\|\mathbf{d}\| = 1\)
- \(t \geq 0\):参数,\(t=0\) 在光线起点,\(t > 0\) 沿正方向
3.2 隐式表面表示
表面可用以下方式表示:
隐式函数形式: \(f(\mathbf{x}) = 0\)
参数函数形式: \(\mathbf{x} = \mathbf{g}(u, v)\)
3.3 光线-表面相交
将光线方程代入表面方程求解参数 \(t\) 和表面坐标 $$(u, v)$:
隐式表面: \(f(\mathbf{p} + t\mathbf{d}) = 0\)
- 一个方程,一个未知数 \(t\)(单变量方程)
参数表面: \(\mathbf{p} + t\mathbf{d} = \mathbf{g}(u, v)\)
- 三个方程,三个未知数 $$(t, u, v)$(多变量方程)
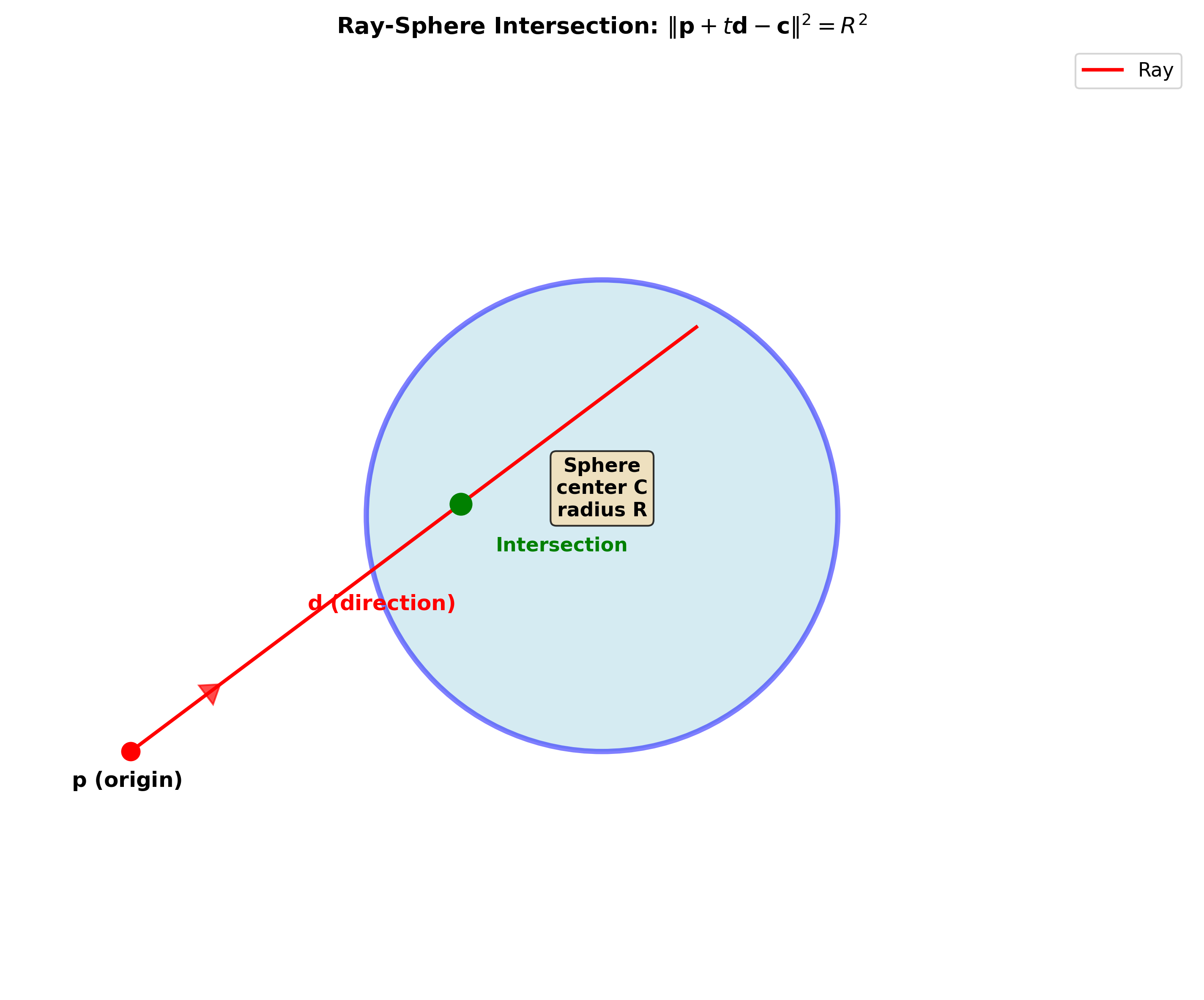
3.4 光线-球体相交
球体隐式方程(球心在原点): \(x^2 + y^2 + z^2 - R^2 = 0\)
代入光线方程: \((p_x + td_x)^2 + (p_y + td_y)^2 + (p_z + td_z)^2 - R^2 = 0\)
展开为关于 \(t\) 的二次方程: \(At^2 + Bt + C = 0\)
其中:
- \(A = d_x^2 + d_y^2 + d_z^2 = 1\)(假设方向向量单位化)
- \[B = 2(p_x d_x + p_y d_y + p_z d_z) = 2\mathbf{p} \cdot \mathbf{d}\]
- \[C = p_x^2 + p_y^2 + p_z^2 - R^2 = \|\mathbf{p}\|^2 - R^2\]
求解: \(t = \frac{-B \pm \sqrt{B^2 - 4C}}{2} = -\mathbf{p} \cdot \mathbf{d} \pm \sqrt{(\mathbf{p} \cdot \mathbf{d})^2 - \|\mathbf{p}\|^2 + R^2}\)
判断:
- 判别式 $$\Delta = B^2 - 4C > 0$:光线穿过球体,有两个交点
- 判别式 \(\Delta = 0\):光线与球体相切,一个交点
- 判别式 \(\Delta < 0\):光线错过球体,无交点
- 取较小的 \(t > 0\) 作为最近交点
3.5 光线-三角形相交
三角形相交包含两个步骤:
-
光线-平面相交:计算光线与三角形所在平面的交点
- 平面方程:\((\mathbf{x} - \mathbf{x}_0) \cdot \mathbf{n} = 0\)
- 代入光线方程求解 \(t\)
-
点在三角形内:使用重心坐标判断交点是否在三角形内
- 重心坐标:\(\mathbf{p} = b_0 \mathbf{x}_0 + b_1 \mathbf{x}_1 + b_2 \mathbf{x}_2\)
- \(b_0, b_1, b_2 \geq 0\) 且 \(b_0 + b_1 + b_2 = 1\) 时点在三角形内
4. 递归光线追踪
4.1 递归光线追踪的思想
从光线投射扩展到递归光线追踪的关键改进:
- 在交点处不仅计算直接光照,还发出反射光线和折射光线
- 递归追踪这些二级光线,找到它们的交点并继续着色
- 所有光线的贡献累加得到最终颜色
4.2 光线类型
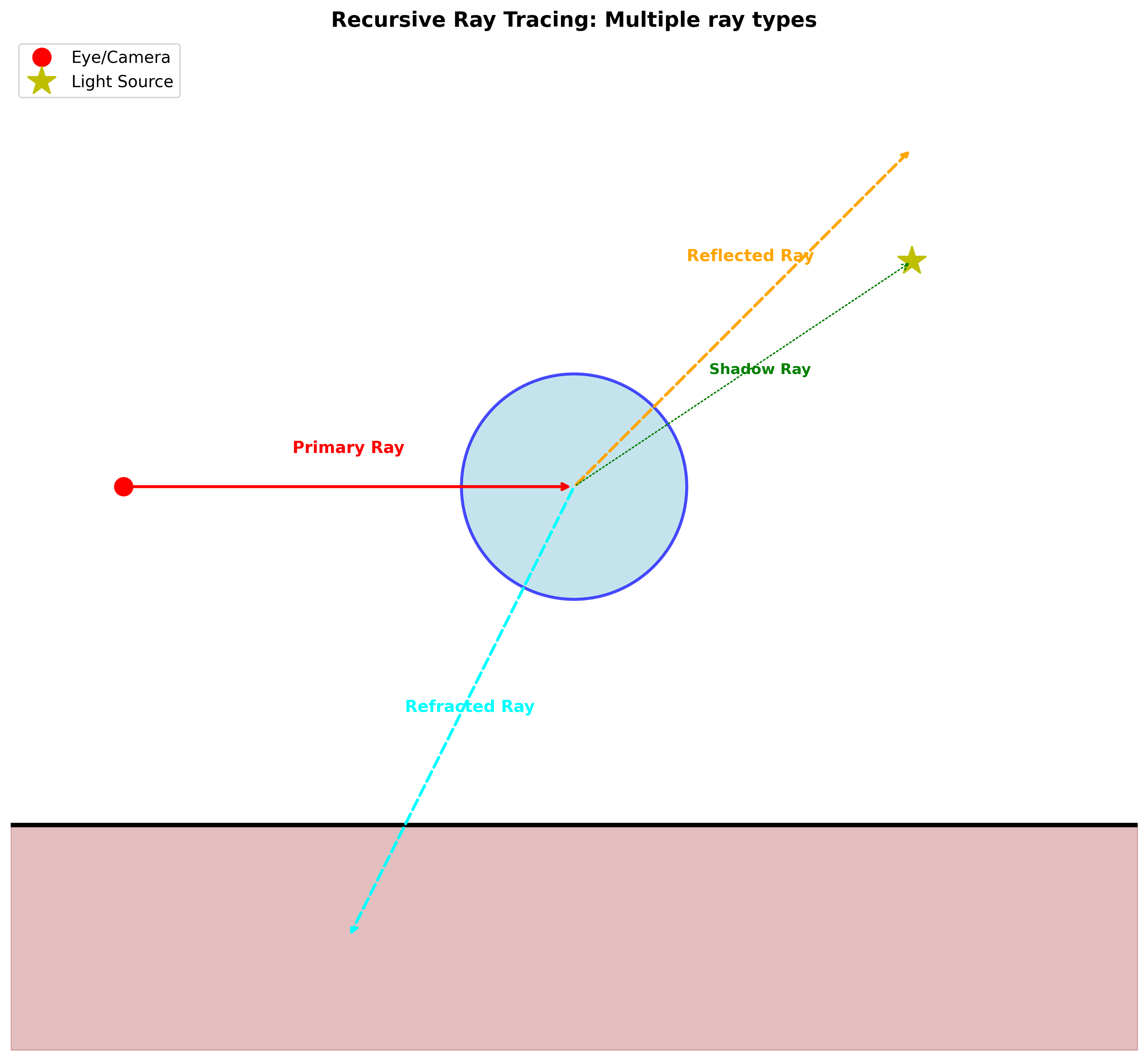
眼睛光线 (Eye Rays)
- 从相机眼睛出发,穿过像素的光线
- 追踪场景中最先击中的表面
阴影光线 (Shadow Rays)
- 从表面点指向光源的光线
- 用于判断该点是否在阴影中
反射光线 (Reflection Rays)
- 从表面点沿镜面反射方向出发
- 用于计算镜面反射贡献
折射光线 (Transmission Rays)
- 从表面点沿折射方向出发
- 用于计算透明物体的折射贡献
4.3 光线树(Ray Tree)
递归光线追踪产生光线树结构:
- 根:眼睛光线
- 内部节点:在交点处分裂出的反射和折射光线
- 叶节点:进入背景或达到最大递归深度的光线
光线树的总贡献即为最终像素颜色。
5. Whitted光线追踪算法
5.1 核心算法
Whitted风格的光线追踪是最基础的递归光线追踪实现:
TraceRay(ray, recursion_depth)
{
// 限制递归深度,避免无限递归
if recursion_depth > MAX_DEPTH:
return BLACK
// 找最近交点
intersection = Closest_Intersection(ray, scene)
if no intersection:
return Background_Color
// 初始化辐度
radiance = ZERO
// 计算直接光照
for each light_source:
shadow_ray = Ray(intersection.point, light_source)
if not IsInShadow(shadow_ray):
radiance += PhongIllumination(intersection, light_source)
// 计算镜面反射
if material.specular_reflectance > 0:
reflected_ray = ComputeReflectedRay(intersection)
radiance += material.specular_reflectance *
TraceRay(reflected_ray, recursion_depth + 1)
// 计算镜面折射
if material.specular_transmittance > 0:
refracted_ray = ComputeRefractedRay(intersection)
radiance += material.specular_transmittance *
TraceRay(refracted_ray, recursion_depth + 1)
return radiance
}
5.2 算法特点
- 递归性:通过递归调用自身处理多次光反弹
- 递归深度限制:防止无限递归(通常3-5层)
- 能量衰减:每次反射/折射乘以对应系数,自动衰减能量
- 阴影处理:通过阴影光线自动判断是否在阴影中
6. 光线类型和追踪策略
6.1 光线的分类
| 光线类型 | 来源 | 去向 | 用途 |
|---|---|---|---|
| 眼睛光线 | 相机 | 场景 | 确定可见性 |
| 阴影光线 | 表面 | 光源 | 判断阴影 |
| 反射光线 | 表面 | 镜面方向 | 镜面反射 |
| 折射光线 | 表面 | 折射方向 | 透射 |
6.2 追踪策略
树状追踪(Tree Tracing)
- 每个交点处同时追踪反射和折射光线
- 产生光线树,覆盖所有可能的光传播路径
- 计算量随递归深度指数增长
优点:能捕捉所有重要的光学现象 缺点:计算效率低,噪声多
7. 镜面反射与折射
7.1 镜面反射
反射光线方向计算:
已知入射光线方向 \(\mathbf{d}_{in}\) 和表面法线 \(\mathbf{n}\),反射光线方向为:
\[\mathbf{d}_{ref} = \mathbf{d}_{in} - 2(\mathbf{d}_{in} \cdot \mathbf{n})\mathbf{n}\]或者等价地: \(\mathbf{d}_{ref} = -\mathbf{d}_{in} + 2(\mathbf{d}_{in} \cdot (-\mathbf{n}))(-\mathbf{n})\)
性质:
- 入射角 = 反射角
- 反射光线与法线在入射光线同侧
7.2 镜面折射(透射)
Snell定律:
当光线从折射率为 \(n_1\) 的介质进入折射率为 \(n_2\) 的介质时:
\[n_1 \sin\theta_1 = n_2 \sin\theta_2\]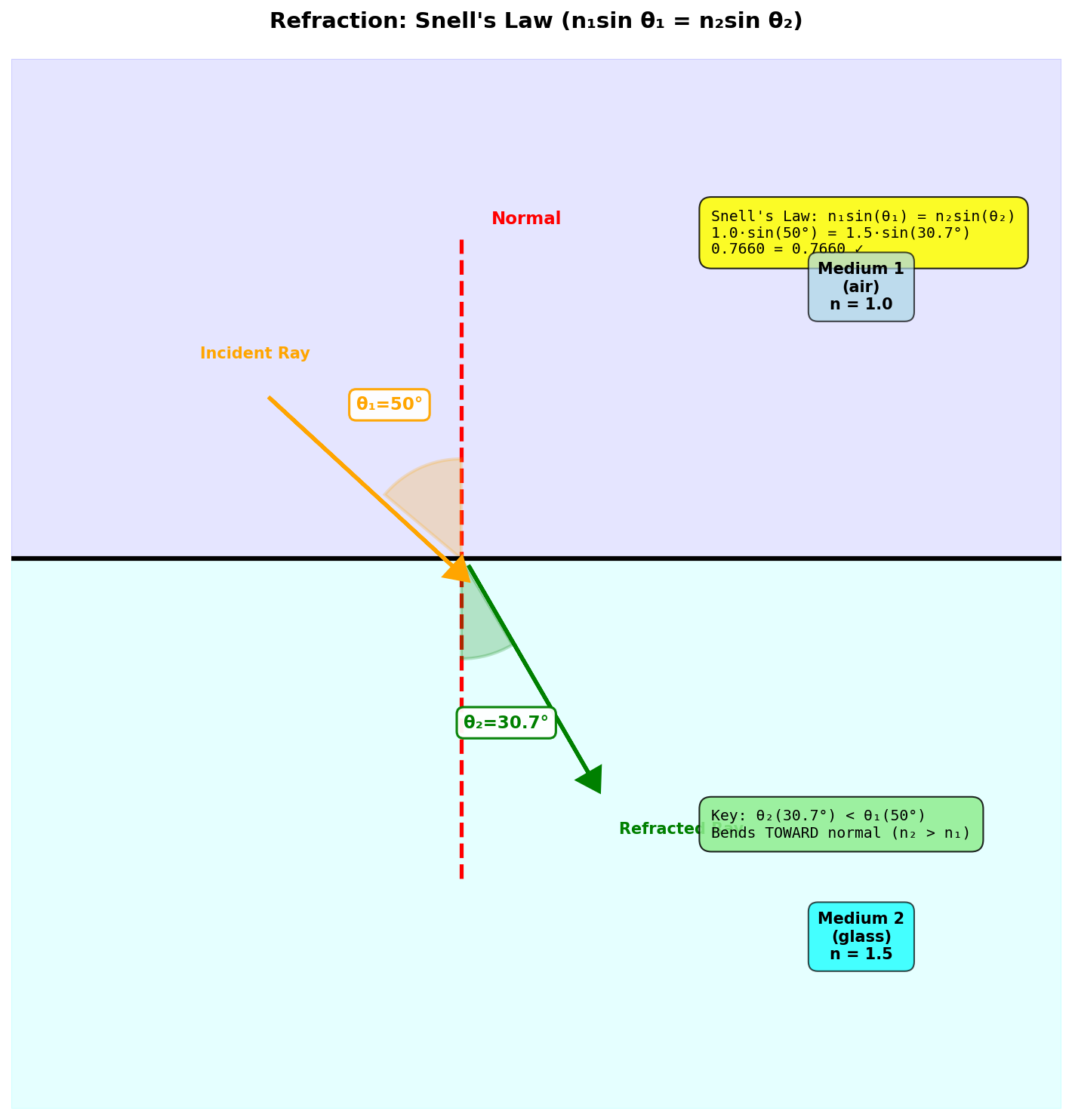
折射光线方向计算:
无需使用三角函数,可以用向量形式:
\[\mathbf{d}_{refr} = \frac{n_1}{n_2}\mathbf{d}_{in} + \left(\frac{n_1}{n_2}\cos\theta_1 - \cos\theta_2\right)\mathbf{n}\]其中: \(\cos\theta_1 = -\mathbf{d}_{in} \cdot \mathbf{n}\) \(\cos\theta_2 = \sqrt{1 - \left(\frac{n_1}{n_2}\right)^2(1-\cos^2\theta_1)}\)
全内反射:
- 当 \(\sin\theta_2 > 1\)(即 $$\cos\theta_2$ 无实数解)时,发生全内反射
- 光线从光学密度更高的介质进入更低密度的介质时可能发生
7.3 常见材料的折射率
| 材料 | 折射率 $n$ |
|---|---|
| 空气/真空 | 1.0 |
| 水 | 1.33 |
| 玻璃 | ≈ 1.5 |
| 钻石 | 2.4 |
8. 抗锯齿
8.1 锯齿问题
光线追踪中的锯齿问题:
- 每个像素仅投射一条光线,代表像素的单一点的颜色
- 但像素代表屏幕上的一个小面积,该面积包含无限个点
- 这些点可能有不同的颜色,导致采样不足和锯齿
8.2 超采样 (Supersampling)
基本方法:
- 为每个像素投射多条光线(例如 3×3 网格)
- 对所有光线的结果进行加权平均
- 使用滤波器(如高斯滤波)进行平滑处理
公式: \(I_{pixel} = \frac{1}{N}\sum_{i=1}^{N} I(x_i, y_i)\)
其中 \((x_i, y_i)\) 是像素内的 \(N\) 个采样点。
8.3 自适应超采样 (Adaptive Supersampling)
对高频区域进行更多采样,对平坦区域采样较少:
算法:
- 将像素分为 2×2 子网格,投射 5 条光线(4 个角 + 1 个中心)
- 比较 5 条光线的颜色是否相似
- 如果相似,使用平均值;如果差异大,递归细分该子网格
- 继续直到子网格颜色均匀或达到最大深度
- 对最终结果应用滤波
优点:
- 自动在复杂区域增加采样密度
- 在平坦区域减少计算量
- 节省总体计算成本
9. 光线追踪加速结构
9.1 加速的必要性
性能瓶颈:
- 对于每条光线,需要测试与场景中所有物体的相交
- 场景包含数百万个三角形时,朴素算法时间复杂度为 \(O(N \cdot M)\)
- \(N\):光线数量
- \(M\):场景中的三角形数量
- 这导致渲染极其缓慢
加速思想:
- 使用空间分割数据结构
- 光线只需测试可能相交的物体
- 在树中进行递归搜索而不是遍历所有物体
9.2 空间分割加速结构
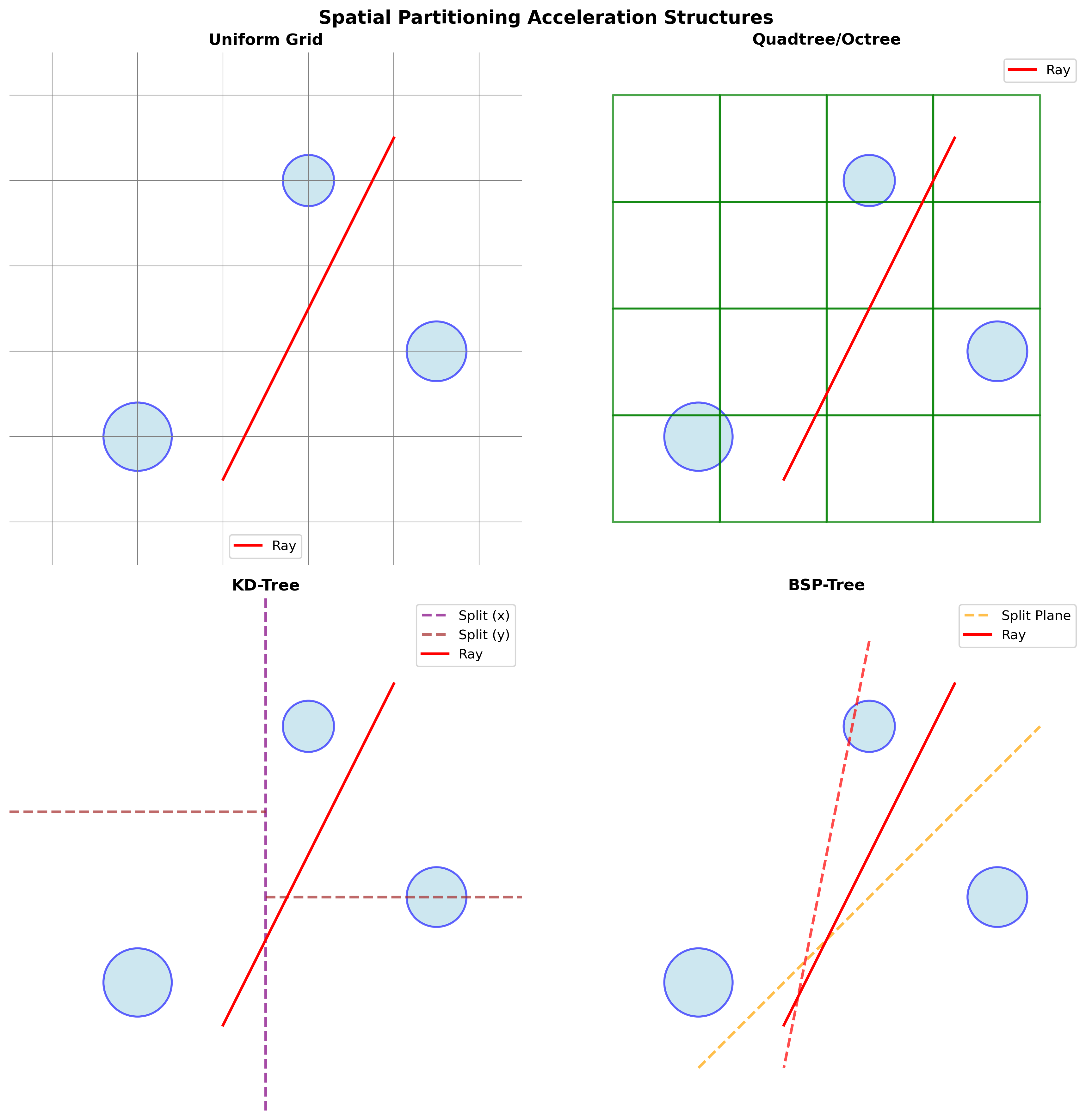
均匀网格 (Uniform Grid)
原理:
- 将场景的包围盒分为规则的立方体网格
- 每个网格单元存储其中包含的物体列表
- 光线遍历网格,只测试当前网格中的物体
优点:
- 实现简单
- 对于均匀分布的场景非常快
缺点:
- 对非均匀场景(物体聚集)效率低
- 可能需要遍历很多空网格
- 内存占用可能很大
八叉树/四叉树 (Octree/Quadtree)
原理:
- 八叉树:3D空间的递归二分,每个节点分为 8 个子立方体
- 四叉树:2D空间的递归二分,每个节点分为 4 个子正方形
- 递归分割直到叶子节点足够简单(包含物体数量少或达到深度限制)
优点:
- 自适应地适应非均匀场景
- 内存占用相对均衡
缺点:
- 比网格遍历稍复杂
- 对于均匀场景可能不如网格快
k-d 树 (KD-Tree)
原理:
- 松弛八叉树的限制
- 每次分割仅沿一个坐标轴(x、y 或 z)
- 不要求分割点在中点
- 选择最优分割点以平衡树的高度
优点:
- 更灵活的分割策略
- 对多种场景都有好的性能
- 广泛用于现代光线追踪器
缺点:
- 构建算法复杂
- 需要选择好的分割策略
二叉空间分割树 (BSP-Tree)
原理:
- 进一步松弛 k-d 树
- 可以用任意超平面进行分割(不仅限于坐标轴平行)
- 在 3D 中用平面分割,在 2D 中用线分割
优点:
- 最灵活的分割方式
- 可以精确适应场景几何
缺点:
- 构建最复杂
- 遍历可能较慢(超平面测试比坐标轴对齐复杂)
- 易产生很多分割后的物体片段
9.3 构建良好的加速结构
关键考虑因素:
-
树的平衡性:避免退化树(所有节点在一侧)
- 平衡树的高度为 \(O(\log N)\)
- 深度过大会导致光线遍历时间长
-
分割数量:权衡树深度和每个节点的物体数
- 分割过多:树深度大,光线遍历开销大
- 分割过少:叶子节点包含太多物体,相交测试开销大
-
物体重叠:物体可能跨越多个节点
- 会导致分割后物体数增加
- BSP 树会产生 O(n³) 个物体片段(最坏情况)
- 改进策略:选择导致最少分割的分割平面
10. 总结
10.1 核心算法流程
光线追踪工作流:
for each pixel (x, y):
ray = Ray(camera, pixel_direction)
color = TraceRay(ray, depth=0)
output_pixel(color)
TraceRay(ray, depth):
if depth > MAX_DEPTH: return BLACK
hit = ClosestIntersection(ray)
if no hit: return BACKGROUND
color = DirectLighting(hit)
color += Reflections(hit, depth)
color += Refractions(hit, depth)
return color
10.2 关键数学公式
| 概念 | 公式 |
|---|---|
| 光线方程 | \(\mathbf{r}(t) = \mathbf{p} + t\mathbf{d}\) |
| 反射 | \(\mathbf{d}_{ref} = \mathbf{d}_{in} - 2(\mathbf{d}_{in} \cdot \mathbf{n})\mathbf{n}\) |
| 折射(Snell) | \(n_1 \sin\theta_1 = n_2 \sin\theta_2\) |
| MIPMAP层级 | \(\text{level} = \log_2(d)\) |
10.3 光线追踪 vs 光栅化
| 特性 | 光线追踪 | 光栅化 |
|---|---|---|
| 全局光照 | ✓ 自然支持 | ✗ 需要近似 |
| 阴影 | ✓ 精确 | ✗ 需要阴影贴图 |
| 反射/折射 | ✓ 精确 | ✗ 需要特殊技巧 |
| 性能 | ✗ 较慢 | ✓ 实时 |
| 实现 | ✓ 相对简单 | ✗ 需要 GPU 优化 |
| 可扩展性 | ✓ 易于扩展 | ✓ 已高度优化 |
10.4 Whitted光线追踪的限制
- 镜面限制:仅处理镜面反射和折射,不能表现粗糙表面
- 递归限制:固定递归深度限制,深度超限后能量丢失
- 采样噪声:每像素一条光线产生高频噪声
- 效率低:计算成本随递归深度指数增长
- 静态照明:预设光源位置,难以处理动态光源
10.5 后续发展方向
- 分布式光线追踪:多条光线采样,减少噪声
- 路径追踪:更强大的递归框架,支持漫反射
- 光子映射:结合光线和粒子的混合方法
- 实时光线追踪:GPU 加速,在游戏中使用
- 深度学习降噪:使用神经网络降低光线追踪的噪声
Enjoy Reading This Article?
Here are some more articles you might like to read next: