VCI - 15: 纹理贴图 (Texture Mapping)

课程: 北京大学视觉计算 (Visual Computing) 2025秋季章节: 第15章纹理贴图内容: 纹理映射、UV坐标系、透视正确插值、纹理采样、MIPMAP、各向异性过滤、纹理应用

1. 纹理贴图概述

1.1 什么是纹理贴图

纹理贴图 (Texture Mapping) 是在图形渲染中，将二维 (2D) 图像应用到三维 (3D) 表面上，以增加视觉细节而无需增加几何复杂度的技术。

核心思想：

通过 2D 纹理而不是复杂的几何模型来表示表面细节
显著降低建模成本和渲染复杂度
使用有限的纹理素 (texel) 覆盖大面积表面

1.2 为什么需要纹理贴图

高效渲染：用低分辨率网格 + 高分辨率纹理替代高分辨率网格
视觉效果：添加颜色、法线、高度等细节信息
现实感：模拟真实世界材料的复杂外观
内存优化：相比存储复杂几何，纹理更节省空间

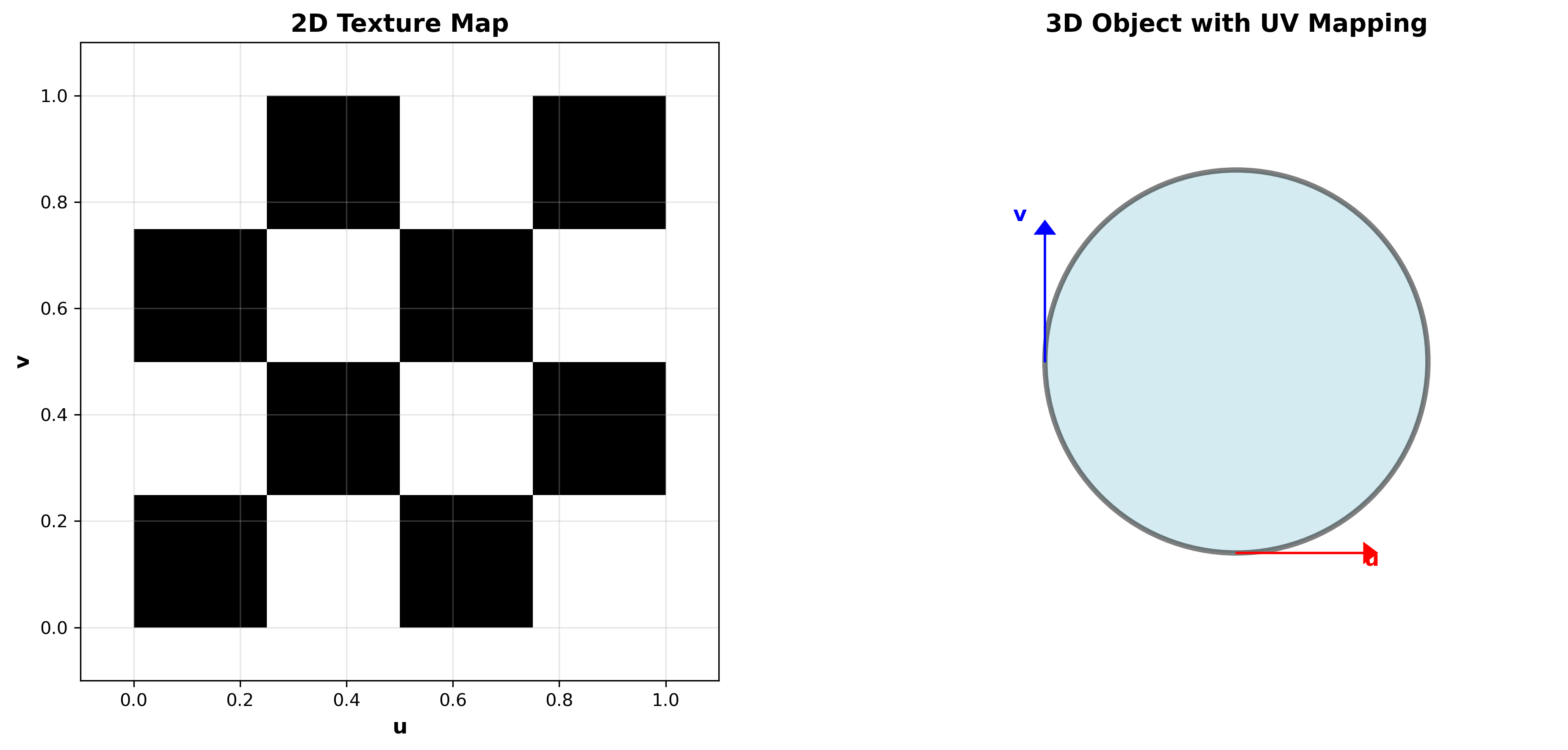
2. UV坐标系统

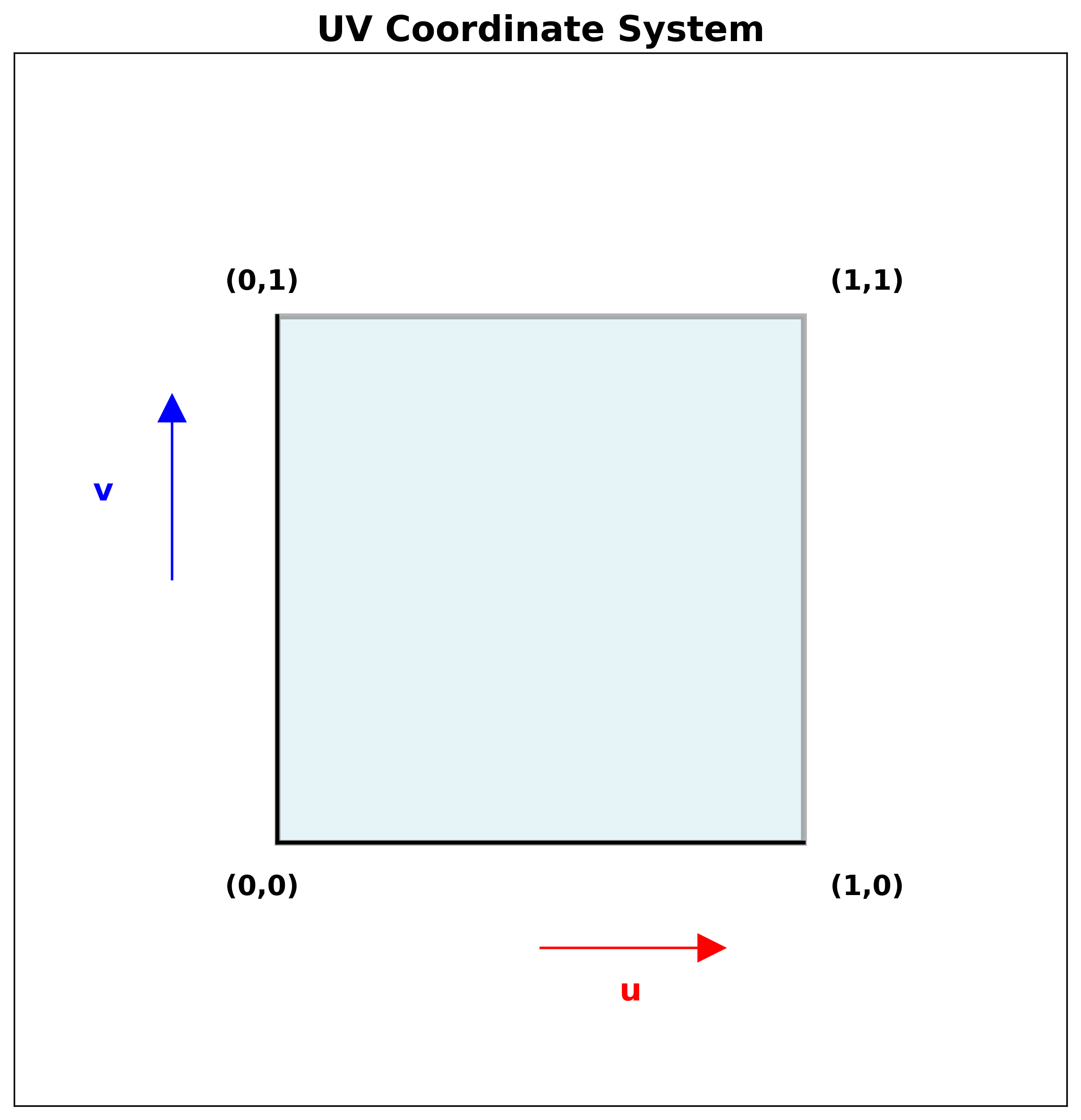
2.1 UV坐标的定义

在纹理空间中，使用二维坐标 $(u, v)$ 表示纹理上的位置，其中：

$u$ 方向：从左到右，范围 $[0, 1]$
$v$ 方向：从下到上，范围 $[0, 1]$
$(0, 0)$：纹理的左下角
$(1, 1)$：纹理的右上角

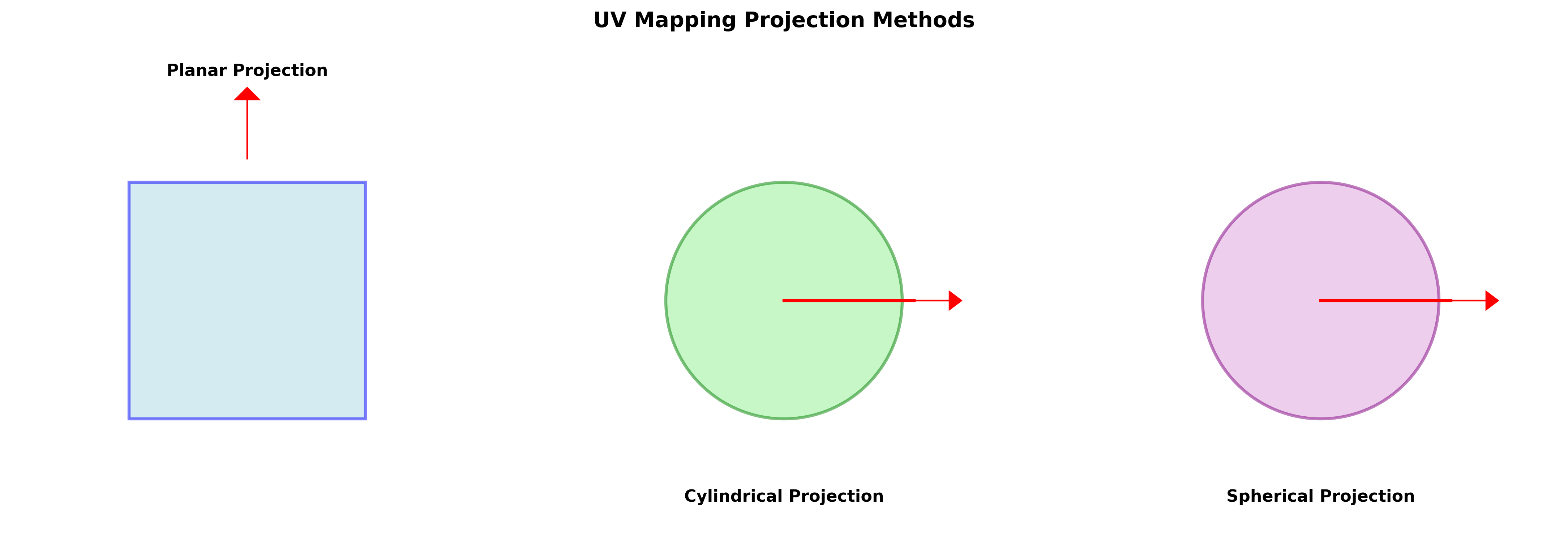
2.2 UV映射方式

不同形状的 3D 模型需要不同的 UV 映射方式：

平面投影 (Planar Projection) $u = x, \quad v = y$ 适用于平面或近似平面的物体

柱面投影 (Cylindrical Projection) $u = \frac{\arctan(y/x)}{2\pi}, \quad v = \frac{z - z_{\min}}{z_{\max} - z_{\min}}$ 适用于圆柱体、圆锥体等旋转对称物体

球面投影 (Spherical Projection) $u = \frac{\arctan(y/x)}{2\pi}, \quad v = \frac{\arcsin(z/r)}{\pi} + 0.5$ 其中 $r = \sqrt{x^2 + y^2 + z^2}$ 为球体半径适用于球体等对称物体

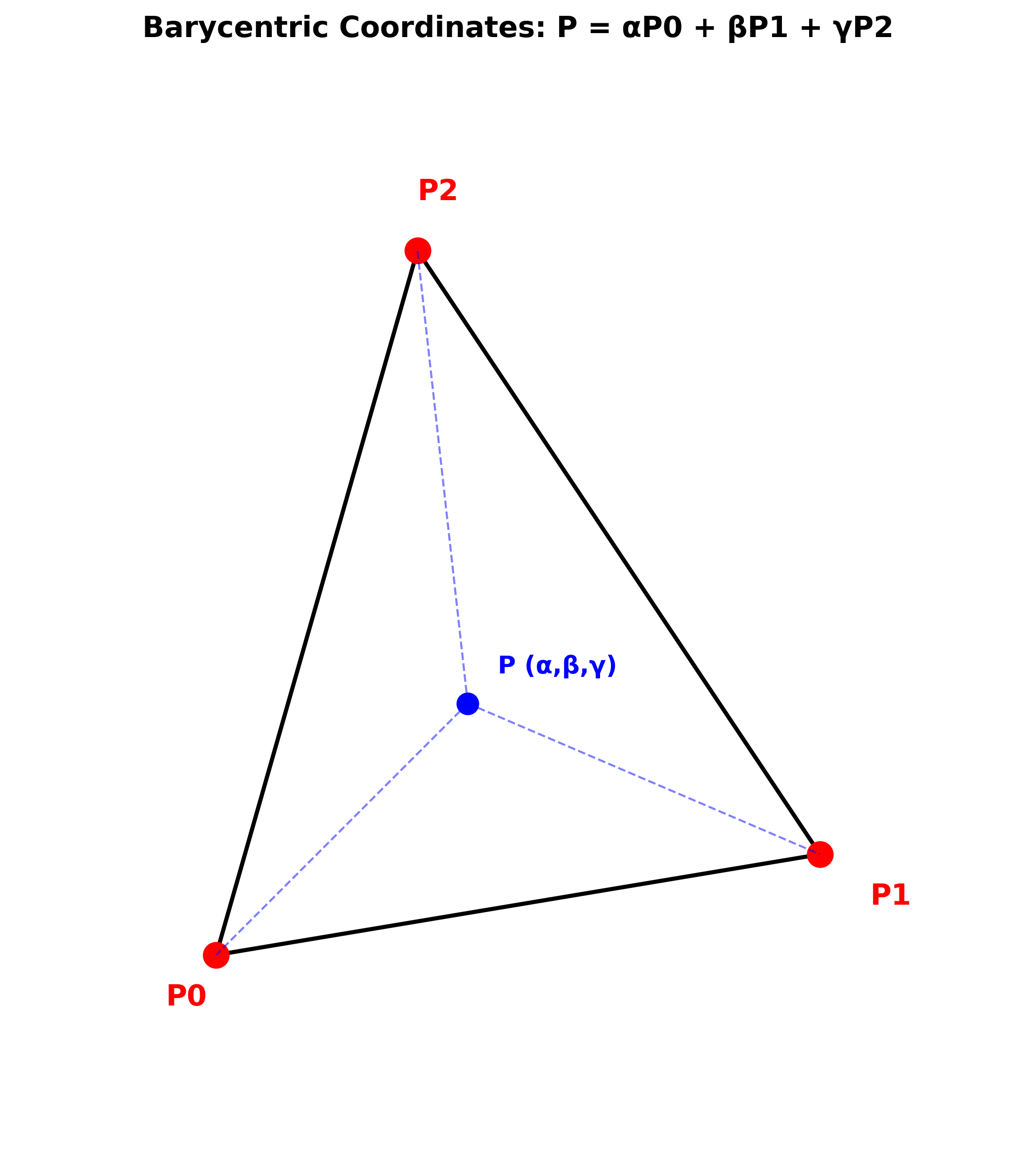
3. 纹理坐标插值

3.1 光栅化阶段的插值

在光栅化过程中，需要为三角形内部的每个像素片段 (fragment) 计算正确的纹理坐标。

给定三角形三个顶点 $P_0, P_1, P_2$ 及其纹理坐标 $(u_0, v_0), (u_1, v_1), (u_2, v_2)$，内部任意点 $P$ 的纹理坐标通过 重心坐标插值 计算：

$u = \alpha u_0 + \beta u_1 + \gamma u_2$ $v = \alpha v_0 + \beta v_1 + \gamma v_2$

其中 $\alpha + \beta + \gamma = 1$，$\alpha, \beta, \gamma$ 是点 $P$ 在三角形中的重心坐标。

4. 透视正确插值

4.1 屏幕空间线性插值的问题

直接在屏幕空间进行线性插值会导致纹理扭曲，特别是在倾斜角度大的表面上。这是因为屏幕空间插值忽略了透视投影的非线性特性。

错误的插值方式： $u_{\text{screen}} = \alpha u_0 + \beta u_1 + \gamma u_2$

4.2 透视正确插值公式

正确的方法是在深度倒数空间进行插值，然后恢复原始值：

\[\frac{1}{z} = \alpha \frac{1}{z_0} + \beta \frac{1}{z_1} + \gamma \frac{1}{z_2}\] \[\frac{u}{z} = \alpha \frac{u_0}{z_0} + \beta \frac{u_1}{z_1} + \gamma \frac{u_2}{z_2}\] \[u = \frac{u/z}{1/z}\]

其中 $z_i$ 是顶点 $$P_i$ 在相机空间中的深度值。

重要性质：

现代图形 API (OpenGL、DirectX) 默认对所有顶点属性执行透视正确插值
法线、颜色、深度等属性也需要透视正确插值
当插值深度值 $z$ 时，实际上插值的是 $\frac{1}{z}$ 的线性函数

5. 纹理采样与过滤

5.1 纹理采样问题

当纹理分辨率与屏幕分辨率不匹配时会产生采样问题：

纹理放大 (Magnification)：一个像素覆盖多个纹素，导致模糊
纹理缩小 (Minification)：多个像素映射到一个纹素，导致锯齿和摩尔纹 (aliasing)

5.2 纹理过滤方法

最近邻过滤 (Nearest Neighbor) $\text{color} = \text{Texture}[\text{round}(u \cdot w), \text{round}(v \cdot h)]$

优点：快速、无模糊
缺点：产生明显的块状和锯齿

双线性过滤 (Bilinear Filtering)

对周围 4 个纹素进行线性插值
公式： $\text{color} = (1-u_f)(1-v_f) \cdot T[u_i, v_i] + u_f(1-v_f) \cdot T[u_i+1, v_i] + (1-u_f)v_f \cdot T[u_i, v_i+1] + u_f v_f \cdot T[u_i+1, v_i+1]$ 其中 $u_i = \lfloor u \cdot w \rfloor$，$u_f = (u \cdot w) - u_i$
优点：平滑、性能好
缺点：距离较远时仍显模糊

三线性过滤 (Trilinear Filtering)

在两个 MIPMAP 层级之间的双线性插值结果再进行插值
在远距离处比双线性更平滑
成本约为双线性的两倍

6. MIPMAP技术

6.1 MIPMAP的定义

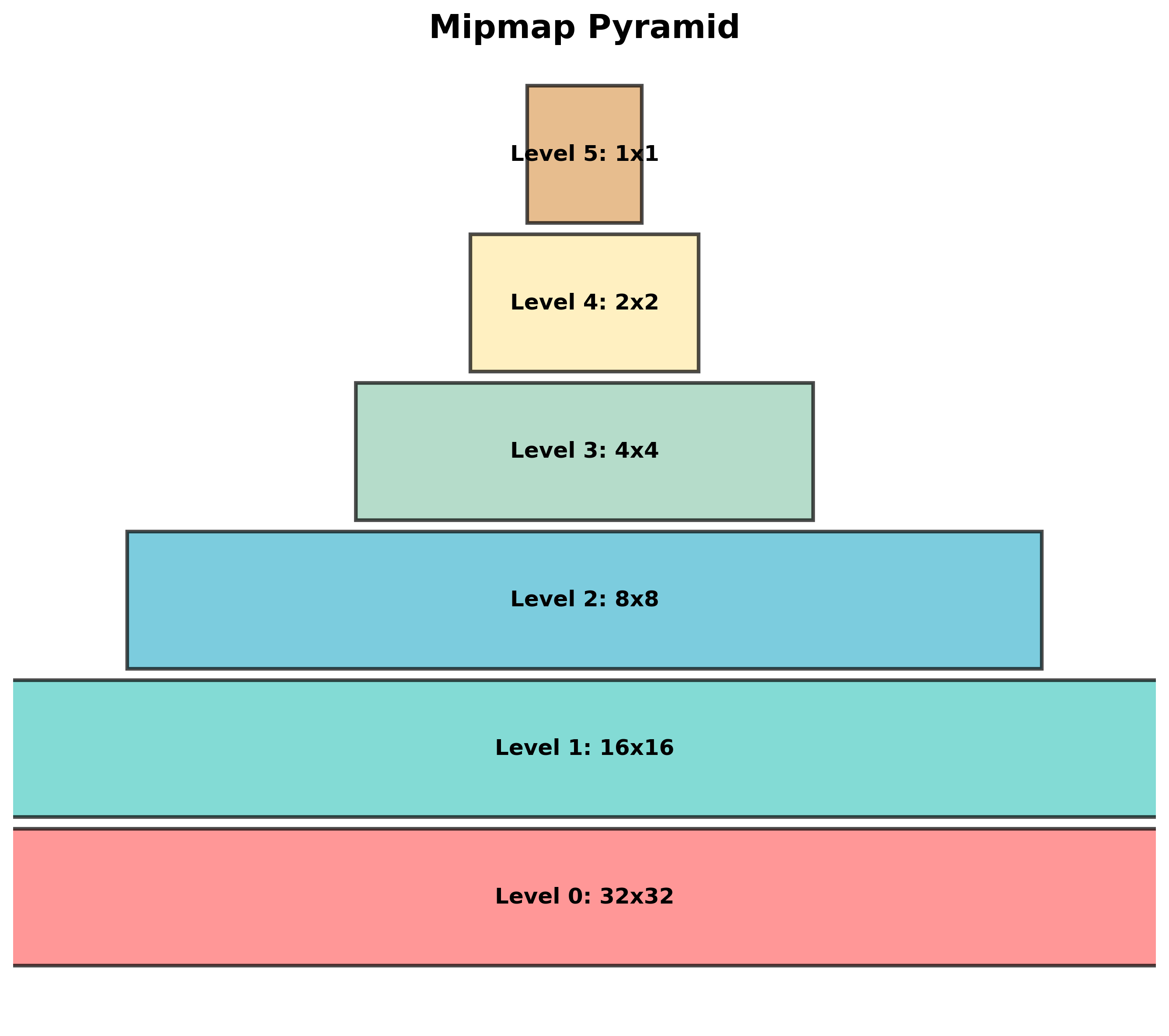
MIPMAP (Multum In Parvo = “much in a small place”) 是一种纹理优化技术，预先计算纹理的一系列逐级缩小版本：

Level 0：原始纹理分辨率 $N \times N$
Level 1：$\frac{N}{2} \times \frac{N}{2}$
Level 2：$\frac{N}{4} \times \frac{N}{4}$
…
Level k：$\frac{N}{2^k} \times \frac{N}{2^k}$

额外内存开销：$1 + \frac{1}{4} + \frac{1}{16} + \cdots = \frac{4}{3} \approx 33\%$

6.2 MIPMAP层级选择

根据像素到表面距离计算应该使用的 MIPMAP 层级：

\[d = \max\left(\sqrt{\left(\frac{\partial u}{\partial x}\right)^2 + \left(\frac{\partial v}{\partial x}\right)^2}, \sqrt{\left(\frac{\partial u}{\partial y}\right)^2 + \left(\frac{\partial v}{\partial y}\right)^2}\right)\] \[\text{level} = \log_2(d)\]

$d < 1$：使用原始纹理（放大）
$d > 1$：使用相应层级的缩小纹理（缩小）

通常使用 三线性过滤 在相邻两个 MIPMAP 层级之间插值，以避免层级之间的突变。

6.3 MIPMAP的优缺点

优点：

显著提升远景纹理的渲染质量
减少摩尔纹和锯齿
提高缓存命中率，改善性能

缺点：

额外的 33% 内存开销
纹理预处理时间增加
对于高度非均匀的表面（如倾斜地面），各向同性 MIPMAP 不够理想

7. 各向异性过滤

7.1 MIPMAP的局限性

各向同性 (Isotropic) MIPMAP 假设纹理在所有方向上的缩放比例相同。但在实际场景中（如倾斜的地面），纹理在不同方向的缩放比例不同：

沿视线方向：缩放比例大（纹理显得很远）
垂直于视线方向：缩放比例小（纹理显得较近）

这导致各向同性过滤在倾斜表面上出现过度模糊。

7.2 各向异性过滤原理

各向异性 (Anisotropic) 过滤 考虑纹理在不同方向的采样率差异，使用 椭圆形采样区域 而不是正方形：

Ripmap 结构：预计算纹理的二维 MIPMAP，同时在两个方向上独立缩放： $\text{Ripmap}[x\text{-level}][y\text{-level}]$

这样可以独立处理 u 和 v 方向的缩放，提供完美的各向异性过滤，代价是内存开销增加到原纹理的约 2/3。

7.3 实际应用

现代 GPU 和图形 API 提供了高效的各向异性过滤实现，通常相比三线性过滤只增加很小的性能开销，但能大幅提升倾斜表面的渲染质量。

8. 纹理的应用方式

8.1 外观纹理 (Appearance Textures)

用于定义物体表面的视觉属性：

颜色/漫反射贴图 (Diffuse/Albedo Map)

存储物体的固有颜色，不包含光照信息
在 PBR (基于物理的渲染) 中称为 Albedo 贴图

粗糙度贴图 (Roughness Map)

灰度图：值越大表示越粗糙（增大高光范围）
影响 BRDF 函数中的微表面分布

金属性贴图 (Metallic Map)

二值图或灰度图：区分金属和非金属区域
金属面：反射率 ≈ 0.5，只有高光反射，无漫反射
非金属：反射率 ≈ 0.04，同时有漫反射和高光反射

8.2 几何纹理 (Geometric Textures)

通过修改表面法线或实际几何来模拟微观表面细节：

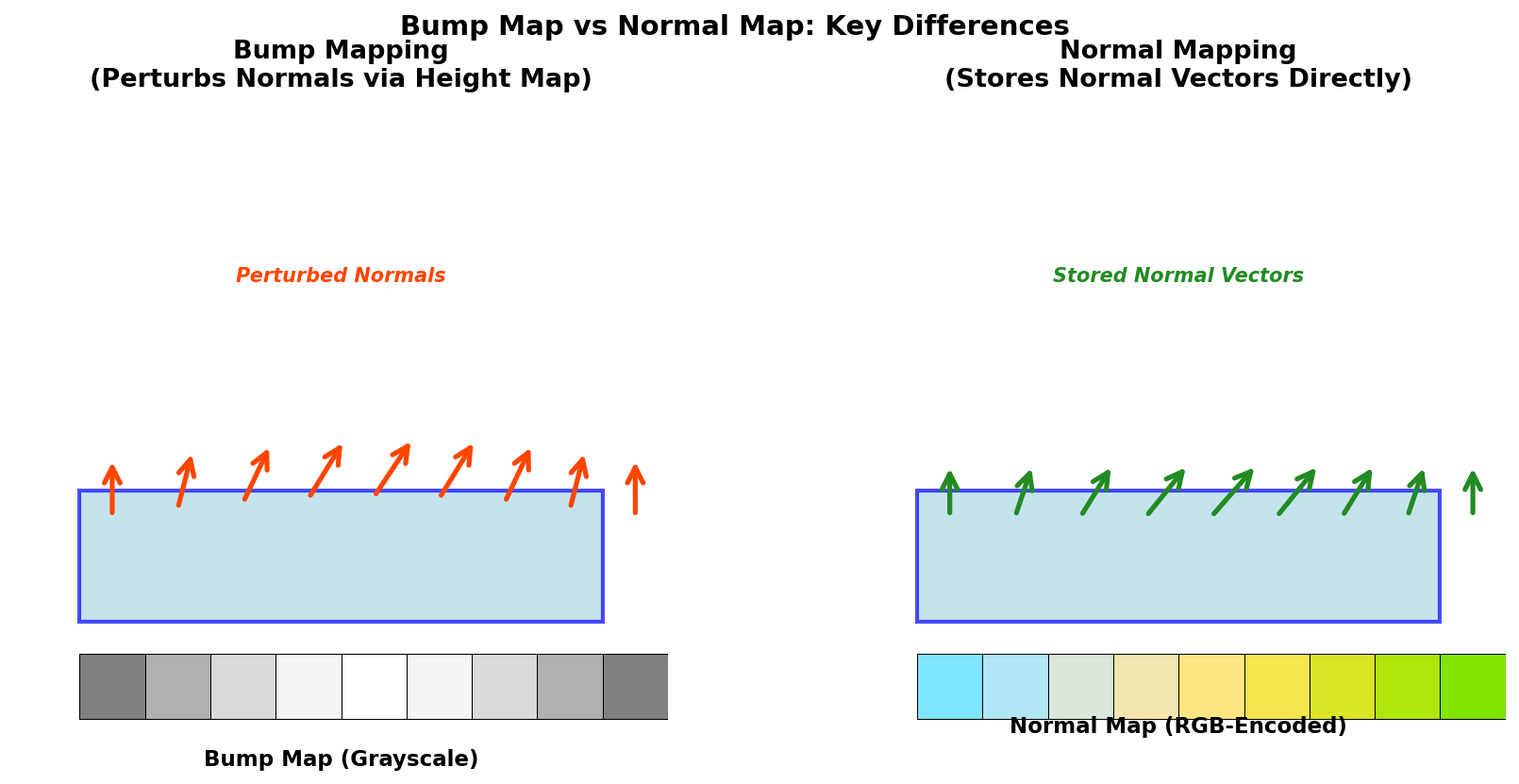
凹凸贴图 (Bump Map)

将灰度值解释为高度信息
通过计算高度场的偏导数修改表面法线： $\mathbf{n}_{\text{perturbed}} = \text{normalize}\left(\mathbf{n} + \frac{\partial h}{\partial u}\mathbf{t} + \frac{\partial h}{\partial v}\mathbf{b}\right)$
优点：计算简单，只需一张灰度贴图
缺点：不改变实际几何，轮廓观看时效果不佳

法线贴图 (Normal Map)

直接存储表面法线，RGB 值编码 XYZ 分量： $\mathbf{n} = (2R-1, 2G-1, 2B-1)$
通常在切线空间 (Tangent Space) 中存储，与模型无关
可复用于不同模型，更节省内存
是现代图形引擎最常用的几何纹理方法

置换贴图 (Displacement Map)

实际改变顶点位置，而不仅是修改法线
需要在运行时或预处理时细分网格
提供最高的视觉保真度，但计算成本最高

8.3 光照纹理 (Lighting Textures)

预计算光照信息，用于实时或离线渲染加速：

阴影贴图 (Shadow Map)

从光源视角渲染场景深度
运行时比较像素深度与阴影贴图深度判断是否在阴影中
是实时阴影计算的标准方法

环境光遮蔽贴图 (Ambient Occlusion, AO)

预计算每个点被环境光遮挡的程度
灰度值：1.0 = 完全亮，0.0 = 完全暗
与漫反射贴图相乘增强细节感

9. 纹理生成方法

9.1 从实景采集

摄影测量 (Photogrammetry)

使用多张照片和 3D 重建算法生成纹理和几何
优点：真实感最强
缺点：需要特殊设备和后处理

激光扫描

使用激光扫描仪获取高精度纹理和几何
常用于建筑、文物等重要场景

9.2 手工编辑与无缝拼接

采集的纹理通常无法直接拼接，需要处理边界：

边界匹配

手工修饰边界，确保无缝过渡
翻转处理：水平或垂直翻转纹理使其边界匹配

纹理合成 (Texture Synthesis)

研究课题：自动生成无缝可拼接的纹理
基于样本纹理的变分方法

9.3 程序生成纹理

Perlin 噪声

连续、自然的伪随机函数
用于生成云、木纹、大理石等自然纹理
实时生成，无需存储

格子噪声 (Cellular Noise)

生成砖块、石头、细胞等有机纹理

分形布朗运动 (Fractional Brownian Motion, fBm)

多层级 Perlin 噪声的组合
模拟自然景物的自相似性

9.4 AI 纹理生成

近年来的发展方向：

文本到纹理 (Text-to-Texture)

输入文本描述（如 “rough wood grain”）
使用扩散模型或生成对抗网络生成纹理
支持实时修改和迭代

示例驱动生成

输入示例纹理和关键词
生成符合风格的新纹理变体

10. 总结

10.1 核心概念回顾

纹理映射流程：

定义 UV 坐标：将 3D 顶点映射到 2D 纹理空间
透视正确插值：在光栅化中以 $\frac{u}{z}$ 形式插值 UV 坐标
纹理采样：根据像素的 UV 坐标读取纹理颜色
过滤与抗锯齿：使用双线性或三线性过滤平滑纹理
应用到着色：将采样得到的颜色应用到片段着色器

10.2 关键技术总结

技术	公式	用途
UV 坐标	投影方程：平面、柱面、球面	建立 3D-2D 映射
透视正确插值	$u = \frac{u/z}{1/z}$	消除透视失真
MIPMAP 层级	$\text{level} = \log_2(d)$	远景纹理抗锯齿
各向异性	椭圆采样、Ripmap	倾斜表面优化

10.3 纹理应用总览

外观：Albedo、Roughness、Metallic
几何：法线贴图、置换贴图
光照：阴影贴图、AO 贴图

10.4 发展趋势

虚拟纹理 (Virtual Texturing)：支持海量纹理的实时流式加载
实时光线追踪与纹理：采样率自适应、重要性采样
AI 驱动生成：自动生成、风格迁移、超分辨率
压缩与优化：新的纹理压缩格式 (ASTC、BC6H 等)
程序化纹理 (Procedural Textures)：节省内存，支持参数化