VCI - 9: 几何处理
9.1 概述
几何处理(Geometry Processing) 是对三维网格模型进行分析、修改和优化的技术。它是计算机图形学中的重要领域,为网格编辑、动画、模拟等应用提供基础。
本章将介绍:
- 离散微分几何基础 - 在离散网格上定义微分算子
- 网格平滑 - 去除噪声,生成光滑表面
- 网格简化 - 降低模型复杂度
- 网格编辑 - 保持细节的形状变形
这些技术是许多高级应用的基础,如角色动画、医学图像处理、CAD/CAM等。
9.2 基础几何操作
在开始离散微分几何之前,我们先回顾一些基础的三维几何操作。
9.2.1 叉积(Cross Product)
给定两个向量\(\mathbf{a}\)和\(\mathbf{b}\),它们的叉积\(\mathbf{c} = \mathbf{a} \times \mathbf{b}\)定义为:
\[\mathbf{c} = \mathbf{a} \times \mathbf{b} = \begin{bmatrix} a_y b_z - a_z b_y \\ a_z b_x - a_x b_z \\ a_x b_y - a_y b_x \end{bmatrix}\]性质:
- \(\mathbf{c} \cdot \mathbf{a} = \mathbf{c} \cdot \mathbf{b} = 0\) (\(\mathbf{c}\)垂直于\(\mathbf{a}\)和\(\mathbf{b}\))
- \(\|\mathbf{c}\| = \|\mathbf{a}\| \cdot \|\mathbf{b}\| \cdot \sin\theta\) (平行四边形面积)
- \(\mathbf{a} \times \mathbf{b} = -\mathbf{b} \times \mathbf{a}\) (反交换律)
- \(\mathbf{a} \times (\mathbf{b} + \mathbf{d}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{d}\) (分配律)
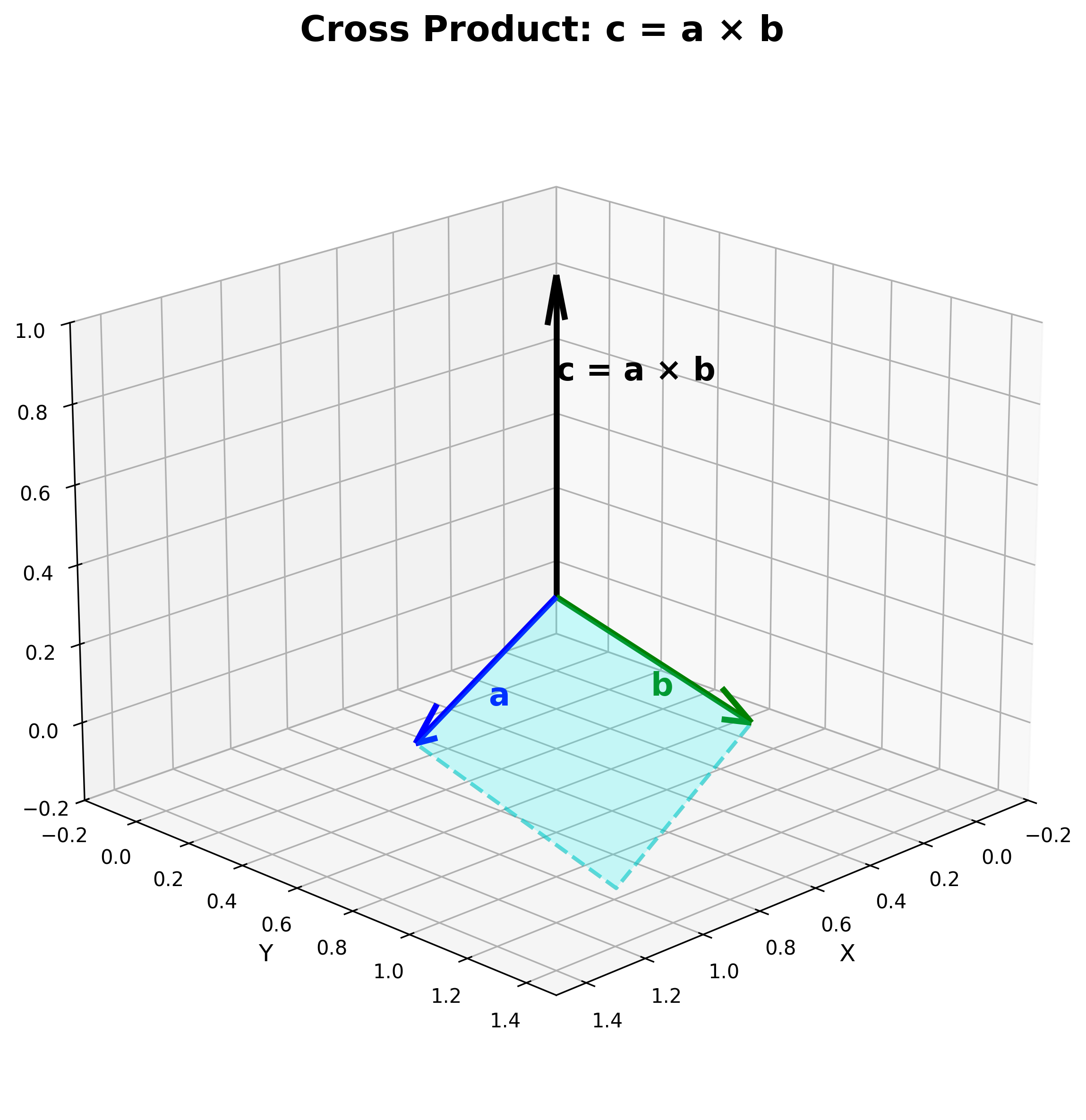
上图展示了叉积的几何意义:向量\(\mathbf{c} = \mathbf{a} \times \mathbf{b}\)垂直于\(\mathbf{a}\)和\(\mathbf{b}\)所在平面,其模长等于平行四边形的面积。
8.2.2 平面方程
参数化表示:给定平面上一点\(\mathbf{o}\)和两个不共线的方向向量\(\mathbf{a}, \mathbf{b}\),平面上任意点可表示为:
\[\mathbf{p} = \mathbf{o} + x\mathbf{a} + y\mathbf{b}, \quad x, y \in \mathbb{R}\]隐式表示:平面也可用方程表示:
\[Ax + By + Cz + D = 0\]其中\((A, B, C)\)是平面的法向量\(\mathbf{n}\)。
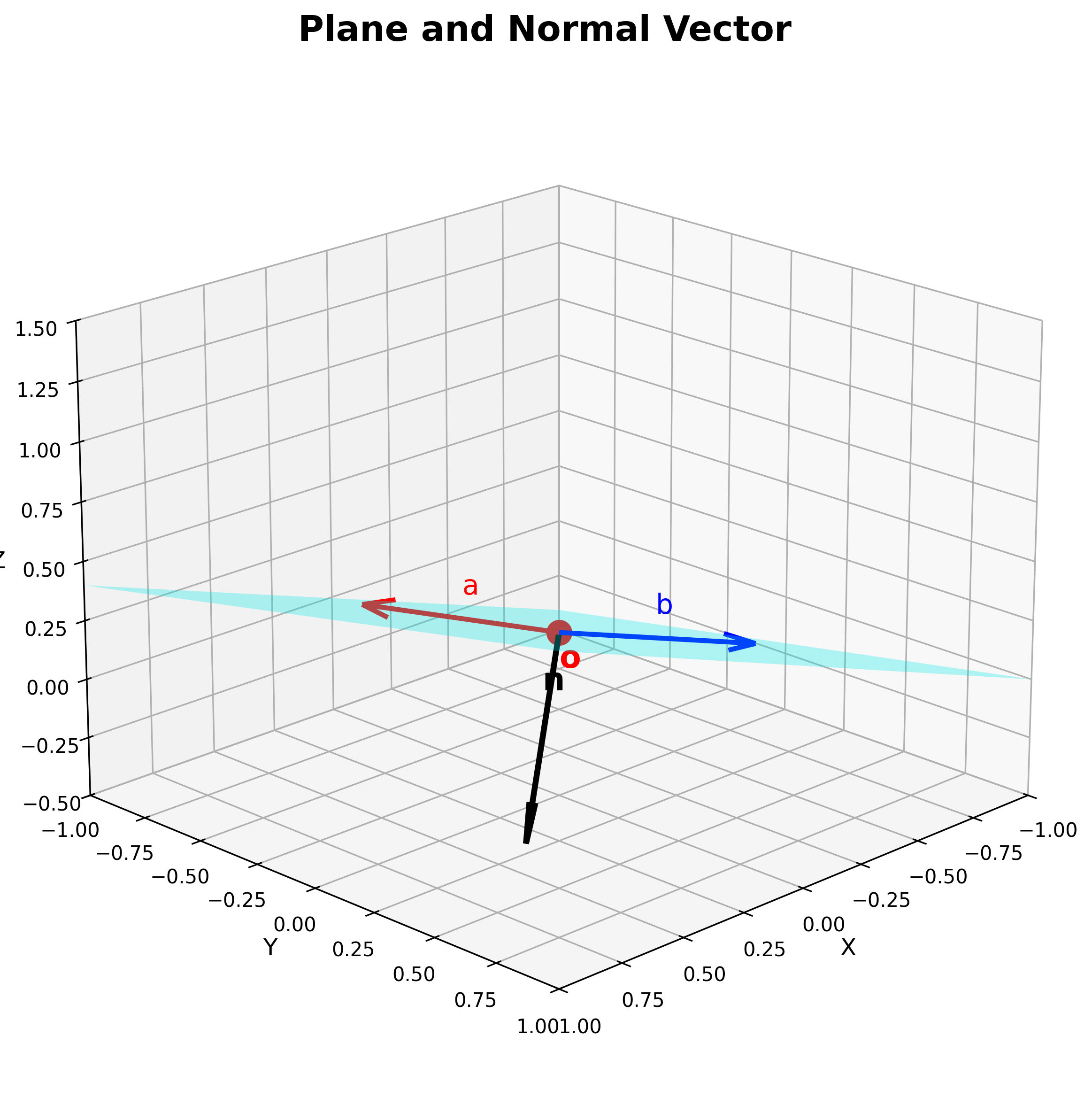
上图展示了平面的法向量\(\mathbf{n}\)以及平面上的两个方向向量\(\mathbf{a}\)和\(\mathbf{b}\)。法向量可通过叉积计算:\(\mathbf{n} = \mathbf{a} \times \mathbf{b}\)。
给定三个非共线点求平面方程:设三点为\(\mathbf{p}_1 = (x_1, y_1, z_1)\),\(\mathbf{p}_2 = (x_2, y_2, z_2)\),\(\mathbf{p}_3 = (x_3, y_3, z_3)\),平面参数可通过行列式计算:
\[A = \begin{vmatrix} 1 & y_1 & z_1 \\ 1 & y_2 & z_2 \\ 1 & y_3 & z_3 \end{vmatrix}, \quad B = \begin{vmatrix} x_1 & 1 & z_1 \\ x_2 & 1 & z_2 \\ x_3 & 1 & z_3 \end{vmatrix}\] \[C = \begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{vmatrix}, \quad D = -\begin{vmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{vmatrix}\]8.2.3 点到平面距离
给定点\(\mathbf{v} = (x_0, y_0, z_0)\)和平面\(Ax + By + Cz + D = 0\),点到平面的距离\(h_d\)为:
\[h_d = \frac{|Ax_0 + By_0 + Cz_0 + D|}{\sqrt{A^2 + B^2 + C^2}}\]也可以用齐次坐标简洁表示:
\[h_d^2 = \tilde{\mathbf{v}}^{\top} \frac{\tilde{\mathbf{n}}\tilde{\mathbf{n}}^{\top}}{\mathbf{n}\mathbf{n}^{\top}} \tilde{\mathbf{v}}\]其中\(\tilde{\mathbf{v}} = (x_0, y_0, z_0, 1)\),\(\tilde{\mathbf{n}} = (A, B, C, D)\),\(\mathbf{n} = (A, B, C)\)。
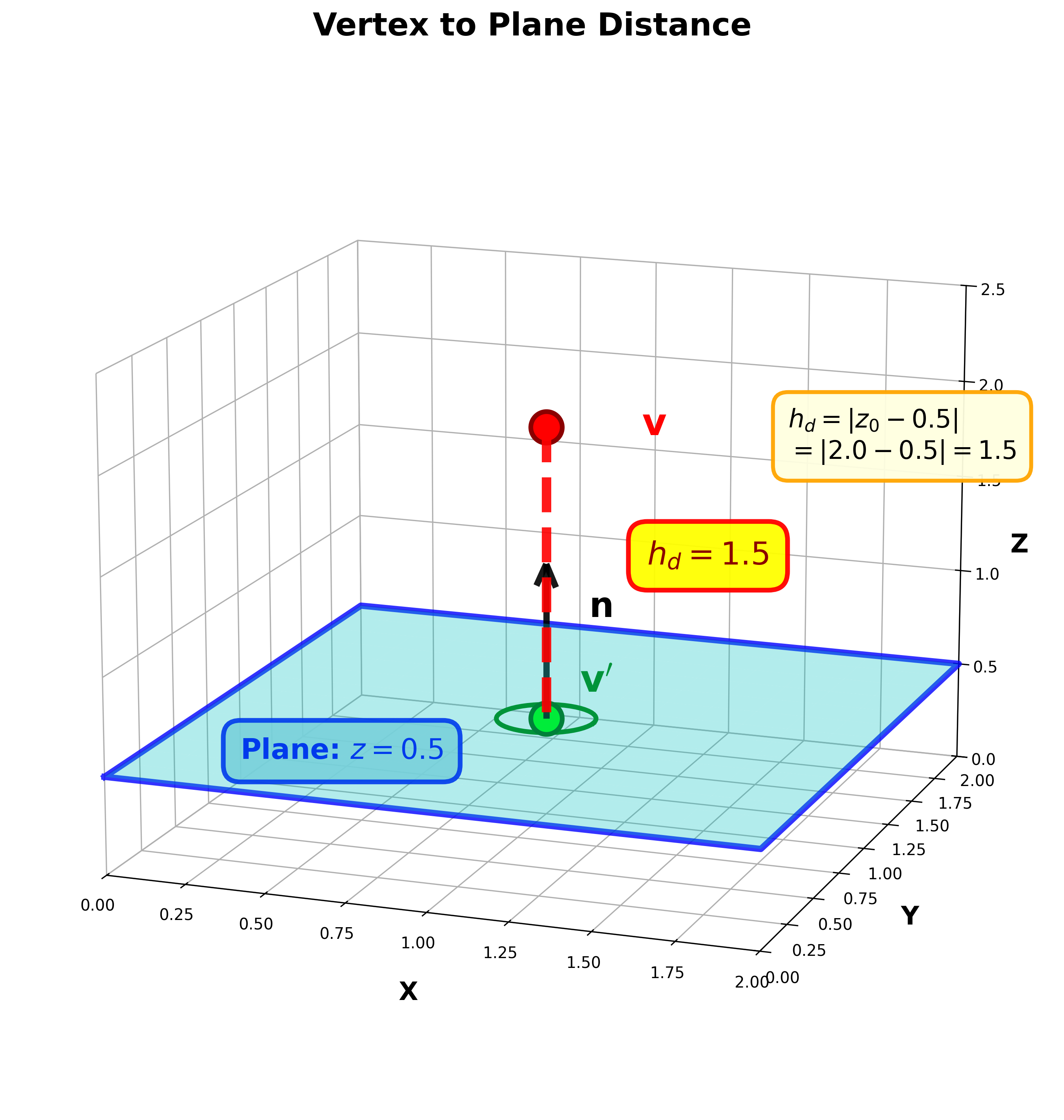
上图展示了点\(\mathbf{v}\)到平面的垂直距离\(h_d\)。点\(\mathbf{v}'\)是\(\mathbf{v}\)在平面上的投影,距离线垂直于平面,平行于法向量\(\mathbf{n}\)。
点与平面的位置关系:设\(s = \mathbf{n} \cdot (\mathbf{p} - \mathbf{o})\),则:
- \(s > 0\):点在平面上方
- \(s = 0\):点在平面上
- \(s < 0\):点在平面下方
8.2.4 直线与三角形相交
判断射线是否与三角形相交的步骤:
- 求出三角形所在平面方程
- 计算射线与平面的交点 \(Q\)
- 判断 \(Q\) 是否在三角形内部
这是光线追踪、碰撞检测等算法的基础操作。
8.3 离散微分几何
8.3.1 概述
离散微分几何(Discrete Differential Geometry, DDG) 是在离散网格上定义和计算微分算子的数学框架。
核心思想:
- 将连续曲面的微分性质(如曲率、梯度、拉普拉斯算子)扩展到离散网格
- 直接从网格数据计算这些性质的近似值
- 为各种几何处理算法提供数学工具
应用:
- 网格滤波与平滑
- 网格参数化
- 形状分析与分割
- 网格重建与重网格化
- 物理模拟
参考资料:Discrete Differential Geometry Course (CMU 15-458)
8.3.2 局部平均区域(Local Averaging Region)
在离散网格上,我们需要在顶点的局部邻域\(\Omega(\mathbf{x})\)内计算空间平均。
常见定义:
- \(n\)-环邻域:从顶点出发,通过边可达的\(n\)跳内的所有顶点
- 测地球:到顶点的测地距离小于某个半径的区域
区域大小的权衡:
- 大邻域:计算稳定,对噪声鲁棒,但可能过度平滑
- 小邻域:对清洁数据精确,但对噪声敏感
常用的局部区域定义:
- 重心单元(Barycentric Cell):由顶点到相邻三角形重心连线围成的区域
- Voronoi单元(Voronoi Cell):到该顶点距离最近的点集
- 混合Voronoi单元(Mixed Voronoi Cell):结合两者优点的混合定义
不同的局部区域定义会影响离散算子的性质。左:重心单元,中:Voronoi单元,右:混合Voronoi单元
8.3.3 法向量(Normal Vectors)
面法向量:对于三角形\(T\),其法向量很容易计算。设三角形三个顶点为\(\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3\),则:
\[\mathbf{n}_T = \frac{(\mathbf{v}_2 - \mathbf{v}_1) \times (\mathbf{v}_3 - \mathbf{v}_1)}{\|(\mathbf{v}_2 - \mathbf{v}_1) \times (\mathbf{v}_3 - \mathbf{v}_1)\|}\]顶点法向量:顶点的法向量通过对相邻三角形法向量进行加权平均得到:
\[\mathbf{n}(v) = \frac{\sum_{T \in \Omega(v)} \alpha_T \mathbf{n}(T)}{\|\sum_{T \in \Omega(v)} \alpha_T \mathbf{n}(T)\|}\]常用权重:
- 均匀权重:\(\alpha_T = 1\)(最简单)
- 面积权重:\(\alpha_T = \text{area}(T)\)(考虑三角形大小)
- 角度权重:\(\alpha_T = \theta(T)\)(顶点在三角形内的角度,最常用)
角度权重通常效果最好,因为它与曲面的内在几何性质相关。
8.3.4 重心坐标(Barycentric Coordinates)
重心坐标是三角形内部点的一种表示方法,在插值和梯度计算中非常重要。
给定三角形顶点\(\mathbf{g}_i, \mathbf{g}_j, \mathbf{g}_k\),三角形内任意点\(\mathbf{g}\)可表示为:
\[\mathbf{g} = \alpha \mathbf{g}_i + \beta \mathbf{g}_j + \gamma \mathbf{g}_k\]其中\(\alpha + \beta + \gamma = 1\),且\(\alpha, \beta, \gamma \geq 0\)。
计算方法:\(\alpha\)等于点\(\mathbf{g}\)对面的小三角形面积与总面积之比:
\[\alpha = \frac{s_i}{s_i + s_j + s_k}\]其中\(s_i\)是\(\mathbf{g}\)、\(\mathbf{g}_j\)、\(\mathbf{g}_k\)围成的三角形面积。
性质:
- 顶点处重心坐标为\((1, 0, 0)\)、\((0, 1, 0)\)、\((0, 0, 1)\)
- 重心(质心)处坐标为\((\frac{1}{3}, \frac{1}{3}, \frac{1}{3})\)
- 可用于线性插值:\(f(\mathbf{g}) = \alpha f_i + \beta f_j + \gamma f_k\)
8.3.5 梯度(Gradients)
给定三角形顶点上的函数值\(f_i, f_j, f_k\),我们可以计算三角形内的梯度\(\nabla f\)。
由于函数在三角形内是分片线性的:
\[f(\mathbf{x}) = \alpha f_i + \beta f_j + \gamma f_k\]梯度为:
\[\nabla_{\mathbf{x}} f(\mathbf{x}) = f_i \nabla_{\mathbf{x}} \alpha + f_j \nabla_{\mathbf{x}} \beta + f_k \nabla_{\mathbf{x}} \gamma\]关键观察:\(\nabla \alpha\)垂直于对边(\(\mathbf{x}_k - \mathbf{x}_j\)),可通过旋转90°得到。
设\(\mathbf{e}_{ij}^{\perp}\)表示边\(\mathbf{e}_{ij}\)逆时针旋转90°,则:
\[\nabla_{\mathbf{x}} \alpha = \frac{(\mathbf{x}_k - \mathbf{x}_j)^{\perp}}{2A_T}\]其中\(A_T\)是三角形面积。类似地:
\[\nabla_{\mathbf{x}} \beta = \frac{(\mathbf{x}_i - \mathbf{x}_k)^{\perp}}{2A_T}, \quad \nabla_{\mathbf{x}} \gamma = \frac{(\mathbf{x}_j - \mathbf{x}_i)^{\perp}}{2A_T}\]最终梯度为:
\[\nabla_{\mathbf{x}} f(\mathbf{x}) = f_i \frac{(\mathbf{x}_k - \mathbf{x}_j)^{\perp}}{2A_T} + f_j \frac{(\mathbf{x}_i - \mathbf{x}_k)^{\perp}}{2A_T} + f_k \frac{(\mathbf{x}_j - \mathbf{x}_i)^{\perp}}{2A_T}\]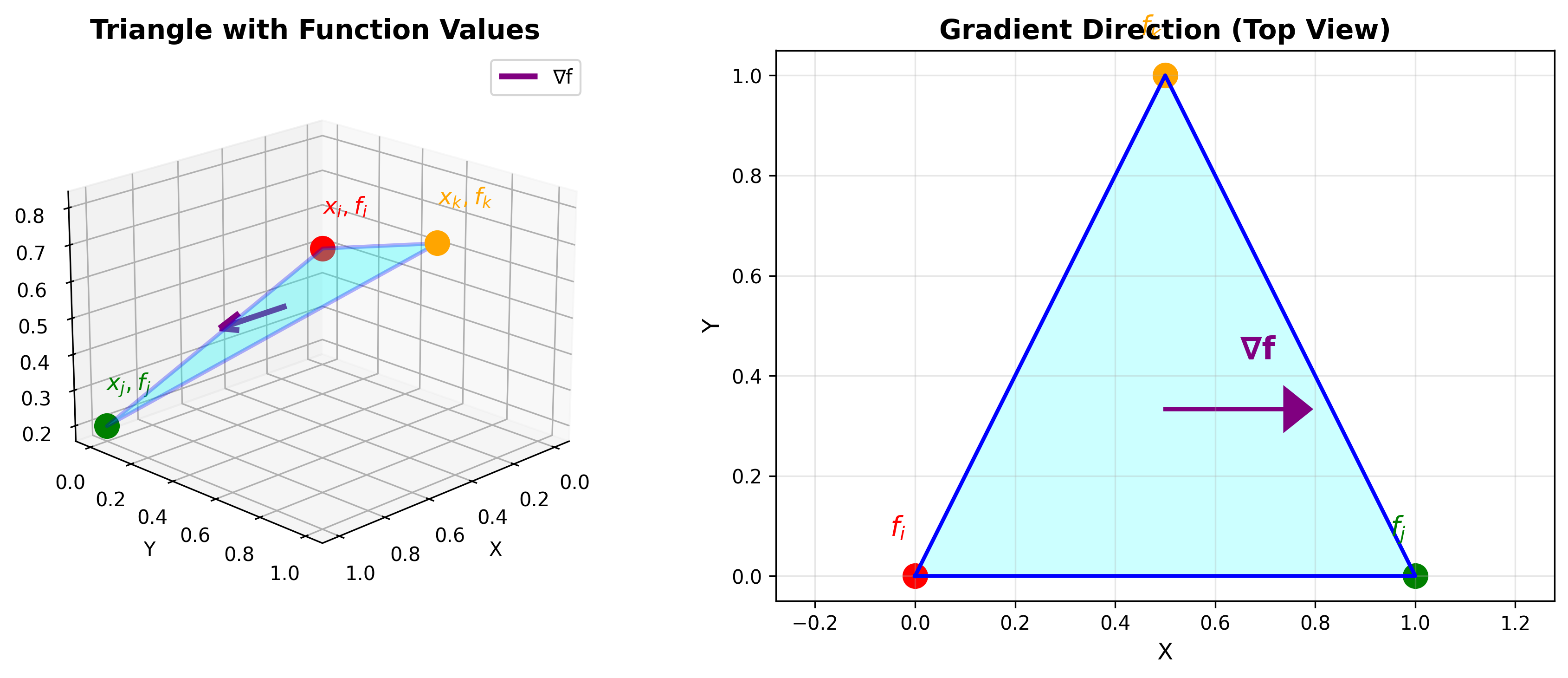
上图展示了在三角形上定义的函数的梯度计算。左图显示三个顶点的函数值,右图显示梯度方向。梯度在每个三角形内是常数。
性质:
- 梯度在每个三角形内是常数
- 梯度方向指向函数增长最快的方向
- 梯度的模表示变化率
8.3.6 拉普拉斯-贝尔特拉米算子(Laplace-Beltrami Operator)
拉普拉斯算子是微分几何中最重要的算子之一:
\[\Delta f = \nabla \cdot \nabla f = \text{div}(\nabla f)\]它表示函数的散度的梯度,或者说二阶导数的迹。
离散拉普拉斯:在顶点\(v_i\)处,函数\(f\)的拉普拉斯近似为:
\[\Delta f(v_i) \approx \frac{1}{A_i} \int_{\Omega_i} \Delta f \, dV\]其中\(\Omega_i\)是顶点\(v_i\)的局部区域,\(A_i\)是该区域的面积。
简化形式:使用格林公式将面积分转化为线积分,可得:
\[(Lf)_i = \sum_{j \in \Omega(i)} \omega_{ij} (f_j - f_i)\]这个公式表示:顶点\(i\)的拉普拉斯值等于其邻居顶点函数值与自身函数值之差的加权和。
常见权重选择:
-
均匀权重(Uniform Laplacian):
\[\omega_{ij} = 1 \quad \text{或} \quad \omega_{ij} = \frac{1}{N_i}\]其中\(N_i\)是顶点\(i\)的邻居数量。
-
余切权重(Cotangent Laplacian): \(\Delta f(v_i) = \frac{1}{2A_i} \sum_{j \in \Omega(i)} (\cot \alpha_{ij} + \cot \beta_{ij})(f_j - f_i)\) 其中\(\alpha_{ij}\)和\(\beta_{ij}\)是边\(ij\)两侧三角形中对边的角。
余切拉普拉斯是使用最广泛的离散化方式,因为它:
- 对各向同性网格精度高
- 保持对称性
- 与连续情况收敛
8.4 梯度与拉普拉斯算子的应用对比
在不同表示上,梯度和拉普拉斯算子有不同的应用:
| 表示 | 梯度 | 拉普拉斯算子 |
|---|---|---|
| 三角网格 | \(\nabla_{\mathbf{x}} f(\mathbf{x}) = f_i \frac{(\mathbf{x}_k - \mathbf{x}_j)^{\perp}}{2A_T} + ...\) 描述网格顶点间的标量场\(f\)变化方向 | \(\Delta f(v_i) = \frac{1}{2A_i} \sum_{j \in \Omega(i)} (\cot \alpha_{ij} + \cot \beta_{ij})(f_j - f_i)\) 描述曲面上的场\(f\)的细节 |
| 2D图像 | \(\nabla f = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix} * f\) 检测图像边缘,表示亮度变化的方向和幅度 | \(\Delta f = \begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix} * f\) 检测高频信息或增强图像中的细节 |
拉普拉斯算子在网格处理中有着广泛应用,包括平滑、去噪、形状分析等。
8.5 网格平滑(Mesh Smoothing)
8.5.1 问题描述
从真实世界获取的三维网格通常包含噪声:
- 扫描设备的测量误差
- 重建算法的近似误差
- 数据传输或存储中的错误
网格平滑的目标是去除噪声,同时保持重要的几何特征。
8.5.2 扩散流(Diffusion Flow)
扩散方程是描述信号随时间平滑过程的数学模型:
\[\frac{\partial f(\mathbf{x}, t)}{\partial t} = \lambda \Delta f(\mathbf{x}, t)\]其中:
- \(f(\mathbf{x}, t)\):\(t\)时刻位置\(\mathbf{x}\)处的信号值
- \(\lambda\):扩散系数(控制平滑速度)
- \(\Delta\):拉普拉斯算子
这个方程描述了热扩散、布朗运动等自然现象。
应用到网格:将顶点坐标\(\mathbf{x}\)视为函数,应用扩散方程:
\[\frac{\partial \mathbf{x}_i(t)}{\partial t} = \lambda \Delta \mathbf{x}_i(t)\]8.5.3 空间离散化
在网格顶点上采样函数值:\(\mathbf{f}(t) = (f(v_1, t), ..., f(v_n, t))^T\)
每个顶点的演化方程:
\[\frac{\partial f(v_i, t)}{\partial t} = \lambda \Delta f(v_i, t)\]矩阵形式:
\[\frac{\partial \mathbf{f}(t)}{\partial t} = \lambda \cdot L\mathbf{f}(t)\]其中\(L\)是拉普拉斯矩阵。
8.5.4 时间离散化
使用显式欧拉积分(Explicit Euler)进行时间离散:
\[\mathbf{f}(t + h) = \mathbf{f}(t) + h \frac{\partial \mathbf{f}(t)}{\partial t} = \mathbf{f}(t) + h\lambda \cdot L\mathbf{f}(t)\]8.5.5 拉普拉斯平滑算法
将任意函数\(\mathbf{f}\)替换为顶点位置\(\mathbf{x}\),得到拉普拉斯平滑:
\[\mathbf{x}_i \leftarrow \mathbf{x}_i + h\lambda \cdot \Delta \mathbf{x}_i\]算法步骤:
- 对每个顶点,计算拉普拉斯\(\Delta \mathbf{x}_i\)(使用均匀或余切权重)
- 更新顶点位置:\(\mathbf{x}_i \leftarrow \mathbf{x}_i + h\lambda \cdot \Delta \mathbf{x}_i\)
- 重复步骤1-2直到达到期望的平滑程度
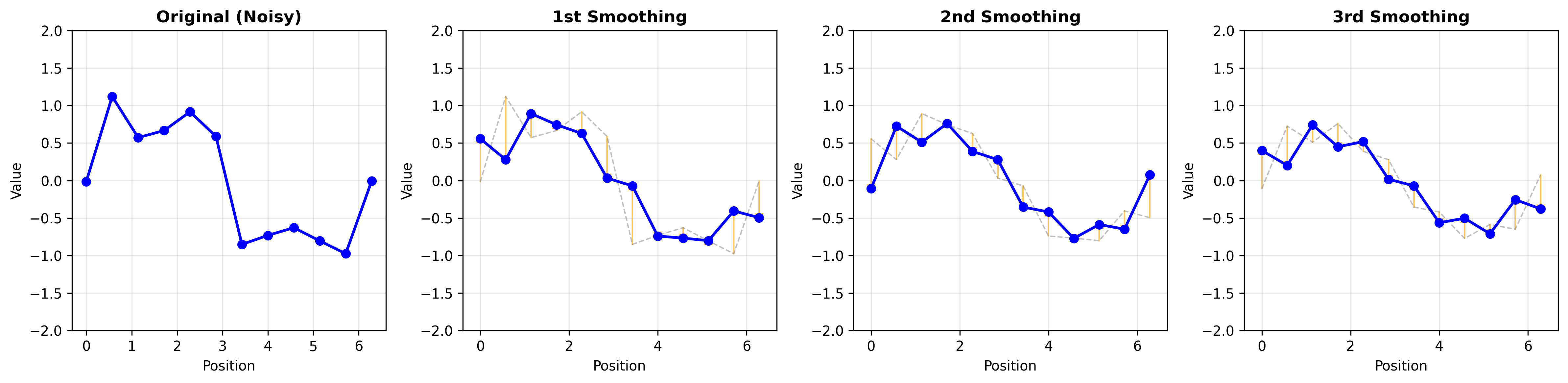
上图展示了拉普拉斯平滑的迭代过程。从左到右:原始含噪声曲线、第1次平滑、第2次平滑、第3次平滑。橙色箭头表示顶点的移动方向。
拉普拉斯的直观解释:
对于均匀拉普拉斯:
\[\Delta \mathbf{x}_i = \frac{\sum_{j \in \Omega(i)} \mathbf{x}_j}{N_i} - \mathbf{x}_i\]这表示:将每个顶点移动到其邻居顶点的平均位置(重心)。
8.5.6 均匀拉普拉斯 vs 余切拉普拉斯
均匀拉普拉斯:
- 将顶点移动到邻居的重心
- 同时平滑几何形状和网格剖分
- 可能导致网格质量下降
余切拉普拉斯:
- 只在法向方向移动,保持切向位置
- 更好地保持几何特征
- 保持网格质量
对比:输入网格(左)、均匀拉普拉斯平滑(中)、余切拉普拉斯平滑(右)。余切拉普拉斯更好地保持了面部特征
8.6 保细节网格编辑(Detail-Preserving Mesh Editing)
8.6.1 动机
在编辑网格时,我们希望:
- 改变整体形状(如拉伸、弯曲)
- 保持局部细节(如皱纹、凹凸)
简单的顶点移动会导致细节丢失或扭曲。
8.6.2 基本思想
关键观察:拉普拉斯坐标编码了局部几何细节。
对于顶点\(i\):
\[\delta_i = \Delta \mathbf{x}_i = \mathbf{L}_i \mathbf{x}\]其中\(\mathbf{L}_i\)是拉普拉斯矩阵的第\(i\)行。
编辑策略:
- 计算原始网格的拉普拉斯坐标\(\boldsymbol{\delta} = L\mathbf{x}\)
- 用户添加建模约束(移动某些顶点)
- 重建满足约束的新网格,同时保持拉普拉斯坐标不变
8.6.3 重建问题
给定:
- 拉普拉斯坐标\(\boldsymbol{\delta}\)
- 约束顶点位置\(\mathbf{x}_i' = \mathbf{u}_i, \quad i \in C\)
求解:新的顶点位置\(\mathbf{x}'\)
优化问题:
\[\mathbf{x}' = \arg\min_{\mathbf{x}'} \left( \|L\mathbf{x}' - \boldsymbol{\delta}\|^2 + \sum_{i \in C} \|\mathbf{x}_i' - \mathbf{u}_i\|^2 \right)\]第一项保持细节(拉普拉斯坐标),第二项满足用户约束。
求解:这是一个线性最小二乘问题,可以通过求解稀疏线性方程组高效求解。
8.6.4 类比:泊松图像编辑
拉普拉斯网格编辑与泊松图像编辑(Poisson Image Editing)有相似之处:
- 泊松编辑:在保持梯度场的同时修改图像区域
- 拉普拉斯编辑:在保持拉普拉斯坐标的同时修改网格形状
两者都通过保持微分信息来保留细节。
8.7 网格简化(Mesh Simplification)
8.7.1 细节层次(Level of Detail, LOD)
在实时渲染中,不同距离的物体需要不同的细节层次:
- 远处物体:使用少量多边形(视觉贡献小)
- 近处物体:使用更多多边形(视觉贡献大)
这种策略可以显著提高渲染性能。
8.7.2 网格简化目标
将给定的多边形网格转换为顶点、边、面更少的网格,同时尽可能保持原始形状。
简化可以:
- 静态:预处理生成多个LOD
- 动态:运行时根据需要简化
8.7.3 简化操作
基本操作:
- 顶点删除(Vertex Removal):删除顶点及相邻面,重新三角化空洞
- 边折叠(Edge Collapse):将边的两个端点合并为一个点
半边折叠(Half-Edge Collapse):
将边的一个端点移动到另一个端点,是最常用的简化操作。
拓扑非法的边折叠:
某些边折叠会导致:
- 非流形结构
- 自相交
- 拓扑变化
需要检测并避免这些情况。
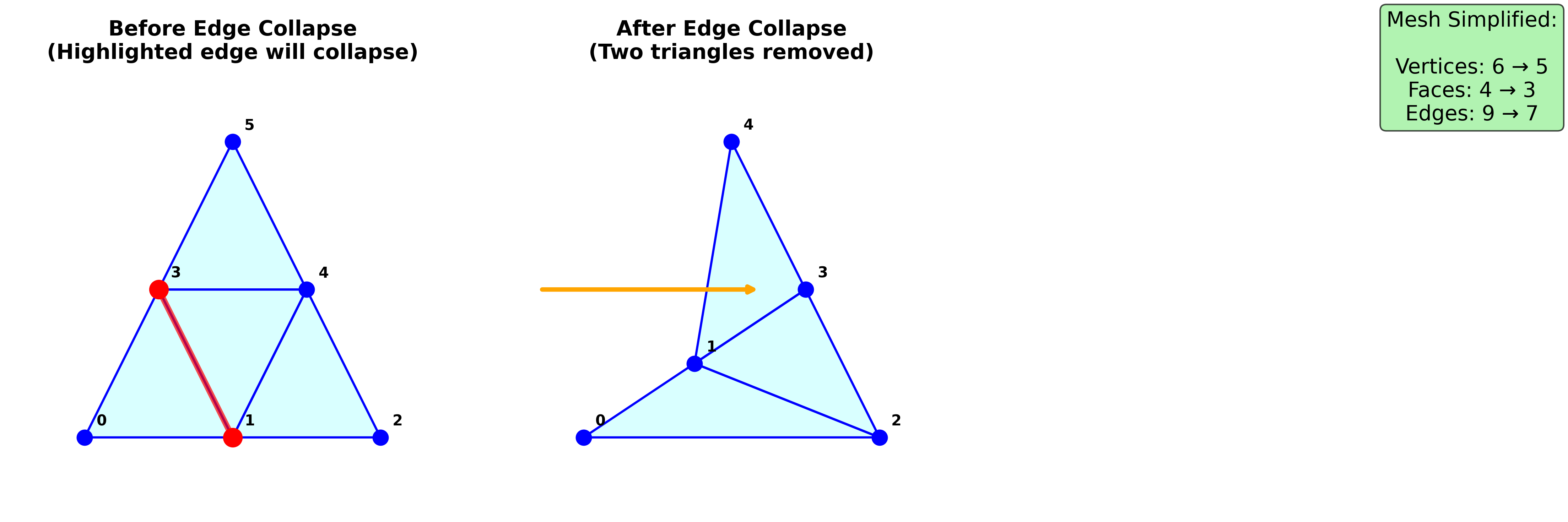
上图展示了边折叠操作。左:折叠前,高亮边将被折叠;中:折叠后,两个顶点合并为一个,两个三角形被移除;右:简化统计信息。
8.7.4 二次误差度量(Quadric Error Metrics, QEM)
核心问题:折叠哪条边?新顶点放在哪里?
Garland & Heckbert 1997 提出的二次误差度量:
思想:新顶点应该最小化到其相关三角形平面的平方距离和。
单个平面的平方距离:
\[h_d^2 = \tilde{\mathbf{v}}^{\top} K_p \tilde{\mathbf{v}}\]其中\(K_p = \tilde{\mathbf{n}}\tilde{\mathbf{n}}^{\top} / (\mathbf{n}\mathbf{n}^{\top})\)。
顶点的二次误差:
对于顶点\(v\),其误差为到所有相关平面距离的和:
\[\text{Error}(\mathbf{v}) = \tilde{\mathbf{v}}^{\top} \sum K_p \tilde{\mathbf{v}} = \tilde{\mathbf{v}}^{\top} Q \tilde{\mathbf{v}}\]其中\(Q = \sum K_p\)是顶点的二次误差矩阵。
算法流程:
初始化:
- 为每个顶点计算二次矩阵\(Q_i\)
- 选择有效的顶点对(边 + 非边)
- 为每对计算最优折叠位置和误差
迭代:
- 选择误差最小的顶点对\((v_1, v_2)\)
- 执行折叠:\(Q_{new} = Q_1 + Q_2\)
- 更新所有涉及\(v_1\)或\(v_2\)的顶点对
特点:
- 快速:使用优先队列管理候选边
- 精确:考虑全局几何误差
- 灵活:可以扩展到纹理、法向量等属性
二次误差的几何意义:
二次误差的等值面是椭球:
- 围绕顶点
- 在曲率小的方向拉伸
- 刻画局部形状
8.8 小结
本章介绍了几何处理的核心技术:
离散微分几何:
- 局部平均区域
- 法向量计算
- 梯度和拉普拉斯算子
- 为网格处理提供数学工具
网格平滑:
- 扩散流方程
- 拉普拉斯平滑
- 均匀 vs 余切权重
- 去除噪声,保持特征
保细节编辑:
- 拉普拉斯坐标编码细节
- 约束优化重建
- 类比泊松图像编辑
网格简化:
- LOD 技术
- 边折叠操作
- 二次误差度量(QEM)
- 保持形状的简化
应用领域:
- 三维建模与动画
- 游戏与虚拟现实
- 医学图像处理
- CAD/CAM
- 数字文化遗产
延伸阅读:
- Discrete Differential Geometry (CMU 15-458) - Keenan Crane
- Surface Simplification Using Quadric Error Metrics - Garland & Heckbert
- Laplacian Surface Editing - Sorkine et al.
几何处理是一个活跃的研究领域,新的算法和应用不断涌现。
Enjoy Reading This Article?
Here are some more articles you might like to read next: