VCI - 8: 几何表示

Created on October 11, 2025

2025   ·   notes   vci   ·   vci

什么是几何

几何学（Geometry） 源自希腊语”geo-metry”，意为”测量地球”。

几何学的定义：

  1. 研究形状、大小、模式和位置的学科
  2. 研究可以测量某些量（长度、角度等）的空间

在计算机图形学中，几何表示是三维建模的核心问题。

经典几何模型示例

Utah Teapot（犹他茶壶）

Utah Teapot 是计算机图形学中最著名的三维模型之一。由Martin Newell于1975年使用贝塞尔曲线创建，现陈列于加州山景城的计算机历史博物馆。这个模型因其适中的复杂度和优雅的形状，成为图形学算法测试的标准模型。

Stanford Bunny（斯坦福兔）

Stanford Bunny 是通过激光扫描重建的网格模型。1994年，Greg Turk在University Ave的一家商店购买了这个雕像，并将其扫描成为计算机图形学研究的标准测试模型。该模型包含约70,000个三角形面片。

计算机中的几何编码方法

在计算机中表示三维几何有两大类方法：

显式表示（Explicit Representation）

特点： 直接给出几何形状的具体表示

常见方法：

  • 点云（Point Cloud） - 物体表面的点集合
  • 多边形网格（Polygon Mesh） - 顶点和面的集合
  • 细分曲面（Subdivision Surface） - 通过细分规则生成
  • 其他 - NURBS、贝塞尔曲面等

优点： 直观、易于处理和渲染

缺点： 存储量大、难以表示复杂拓扑

隐式表示（Implicit Representation）

特点： 通过数学函数或规则定义几何形状

常见方法：

  • Level Set - 等值面表示
  • 代数曲面（Algebraic Surface） - \(f(x,y,z) = 0\)
  • 符号距离函数（SDF） - 到表面的有符号距离
  • 其他 - 分形、构造实体几何（CSG）等

优点： 紧凑、适合布尔运算和变形

缺点： 难以直接渲染、不易控制细节

每种表示方法都适合不同的任务和几何类型。

点云（Point Cloud）

基本概念

点云 是物体表面上采样点的集合，通常由3D扫描设备（如LiDAR激光雷达）获得。

表示方法： \(P = \{(x_i, y_i, z_i)\}_{i=1}^{n}\)

左图展示了Stanford Bunny的点云表示，右图展示了自动驾驶中LiDAR扫描的室内场景点云。点云直观地表示了物体的表面形状。

点云的特点

优点：

  • 最简单的表示方法
  • 直接来自扫描设备
  • 易于获取和存储
  • 适合表示复杂场景

缺点：

  • 不包含拓扑信息
  • 难以进行几何处理
  • 渲染效果较差（离散点）
  • 数据量大且冗余

应用场景：

  • 自动驾驶感知
  • 三维重建
  • 逆向工程
  • 文物数字化

多边形网格（Polygon Mesh）

基本概念

多边形网格 可能是计算机图形学中最常用的几何表示方法。

核心思想： 用多边形（通常是三角形或四边形）的集合来逼近曲面。物体表面被分解为多边形面片的集合，每个面片由顶点、边和面组成。

多边形网格的特点

优点：

  • 渲染速度快（GPU硬件加速）
  • 易于进行几何处理
  • 支持自适应采样
  • 数据结构成熟

缺点：

  • 表示光滑曲面需要大量多边形
  • 数据结构较复杂
  • 拓扑变化不易处理

三角形网格（Triangle Mesh）

为什么选择三角形？

三角形是最基本的多边形：

  • 任何三个不共线的点确定唯一平面
  • 必然是平面的（不会扭曲）
  • 任何多边形都可以三角化
  • 重心坐标插值简单
  • GPU硬件原生支持

三角形网格的数据结构

Wavefront OBJ 文件格式示例（四面体）：

# 顶点列表 (x, y, z)
v -1 -1 -1    # Vertex 0
v  1 -1  1    # Vertex 1
v  1  1 -1    # Vertex 2
v -1  1  1    # Vertex 3

# 面列表 (顶点索引，从1开始)
f 1 3 2       # Face 1
f 1 4 3       # Face 2
f 4 1 2       # Face 3
f 4 2 3       # Face 4

方法1：分离三角形（Triangle Soup）

存储方式： 直接存储每个三角形的三个顶点坐标

tris[0] = {(x0,y0,z0), (x2,y2,z2), (x1,y1,z1)}
tris[1] = {(x0,y0,z0), (x3,y3,z3), (x2,y2,z2)}
...

优点： 简单、易于实现

缺点： 包含大量冗余顶点信息（共享顶点被重复存储）

方法2：索引三角形集（Indexed Triangle Set）

存储方式：

  • 顶点列表：存储所有顶点的坐标
  • 三角形列表：存储三角形的顶点索引

示例：

verts[0] = (x0, y0, z0)
verts[1] = (x1, y1, z1)
verts[2] = (x2, y2, z2)
...

tind[0] = (0, 2, 1)
tind[1] = (0, 3, 2)
...

优点：

  • 共享顶点位置信息，减少内存使用
  • 确保网格完整性（修改顶点位置会影响所有相关多边形）

缺点：

  • 数据结构更复杂
  • 查找三角形邻接关系不方便

欧拉定理

对于简单多面体，顶点数\(v\)、边数\(e\)和面数\(f\)满足：

\[v - e + f = 2\]

这个定理可以用于验证网格拓扑的正确性。

半边数据结构（Half-edge Data Structure）

基本思想

核心概念： 将每条边分为两个半边（half-edge），作为连接网格元素的”胶水”。

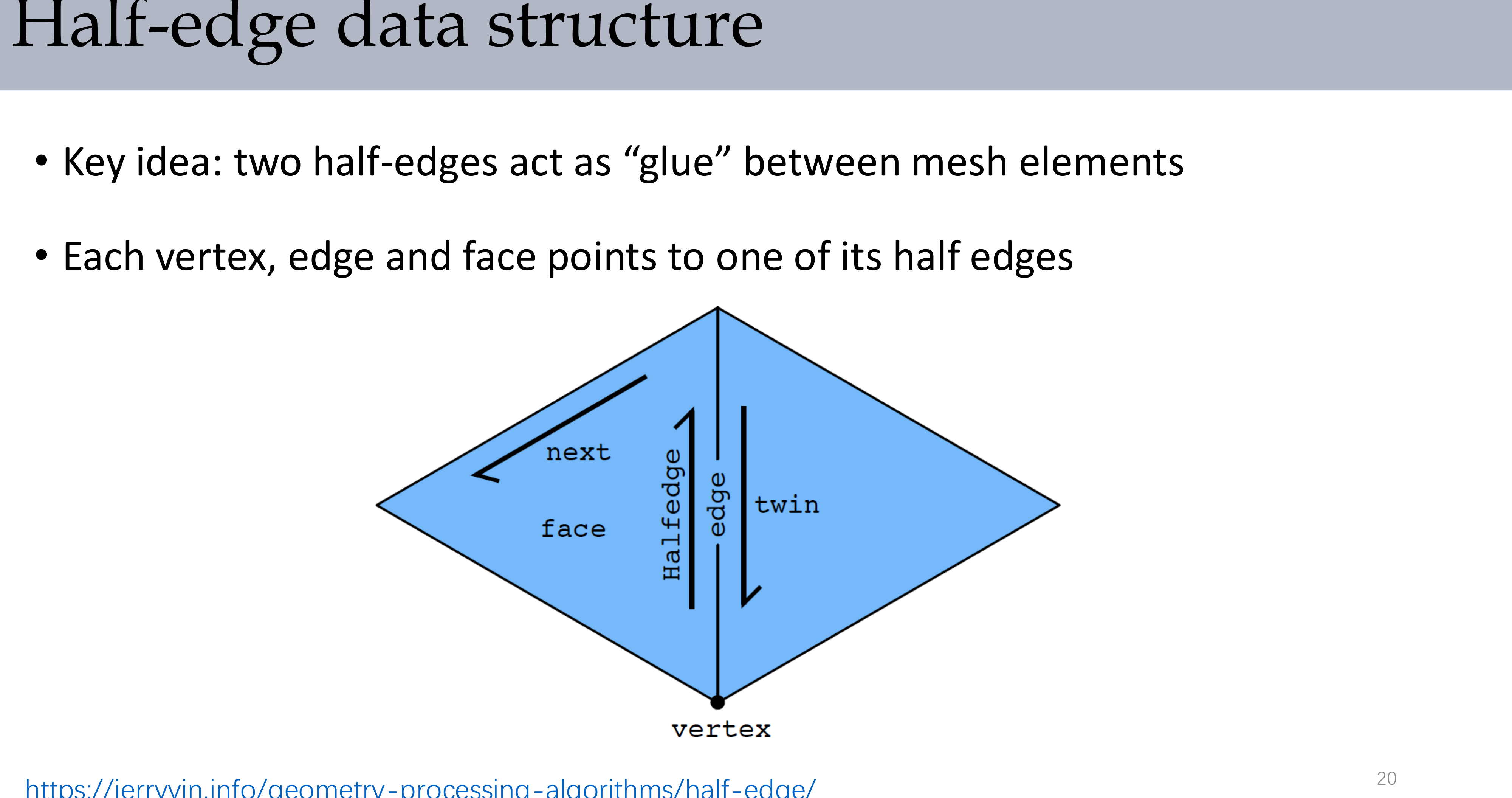
上图展示了半边数据结构的基本元素：每个半边有指向下一个半边（next）、对偶半边（twin）、所属顶点（vertex）、所属边（edge）和所属面（face）的指针。

数据结构定义

struct Halfedge {
    Halfedge *twin;   // 对偶半边
    Halfedge *next;   // 同一面上的下一条半边
    Vertex *vertex;   // 目标顶点
    Edge *edge;       // 所属边
    Face *face;       // 所属面
};

struct Vertex {
    Vec3 pos;         // 顶点坐标
    Halfedge *halfedge; // 任一出发的半边
};

struct Edge {
    Halfedge *halfedge; // 任一半边
};

struct Face {
    Halfedge *halfedge; // 任一边界半边
};

使用示例

示例1：遍历一个面的所有顶点

Halfedge* h = f->halfedge;
do {
    do_work(h->vertex);
    h = h->next;
} while (h != f->halfedge);

示例2：遍历一个顶点周围的所有边

Halfedge* h = v->halfedge;
do {
    do_work(h->edge);
    h = h->twin->next;
} while (h != v->halfedge);

优点：

  • 快速查询邻接关系
  • 支持高效的网格遍历
  • 方便实现复杂的几何操作

缺点：

  • 存储开销较大
  • 实现复杂

四边形网格（Quad Mesh）

四边形网格的特点：

优点：

  • 规则性好，易于存储
  • 易于参数化（天然的UV坐标）
  • 适合纹理映射
  • 更符合人工建模习惯

缺点：

  • 限制更强（不是所有曲面都适合）
  • 生成高质量四边形网格是研究难题

应用：

  • 角色建模
  • CAD设计
  • 参数化曲面建模

细分曲面（Subdivision Surface）

基本思想

细分曲面 通过对粗糙网格的逐步细化，生成光滑曲面的极限形式。从粗糙的控制网格开始，通过迭代应用细分规则，逐步增加网格的顶点和面数，最终收敛到光滑的极限曲面。

Catmull-Clark细分

适用对象： 四边形网格

细分规则：

  1. 添加面点（Face Point）
\[f = \frac{v_1 + v_2 + v_3 + v_4}{4}\]
  1. 添加边点（Edge Point）
\[e = \frac{v_1 + v_2 + f_1 + f_2}{4}\]
  1. 更新顶点（Vertex Point）
\[v' = \frac{1}{n}\left[\frac{f_1+f_2+f_3+f_4}{4} + 2\frac{m_1+m_2+m_3+m_4}{4} + (n-3)p\right]\]

其中：

  • \(n\)：顶点度数（相邻面/边数）
  • \(f_i\)：相邻面点
  • \(m_i\)：相邻边中点
  • \(p\)：原顶点位置

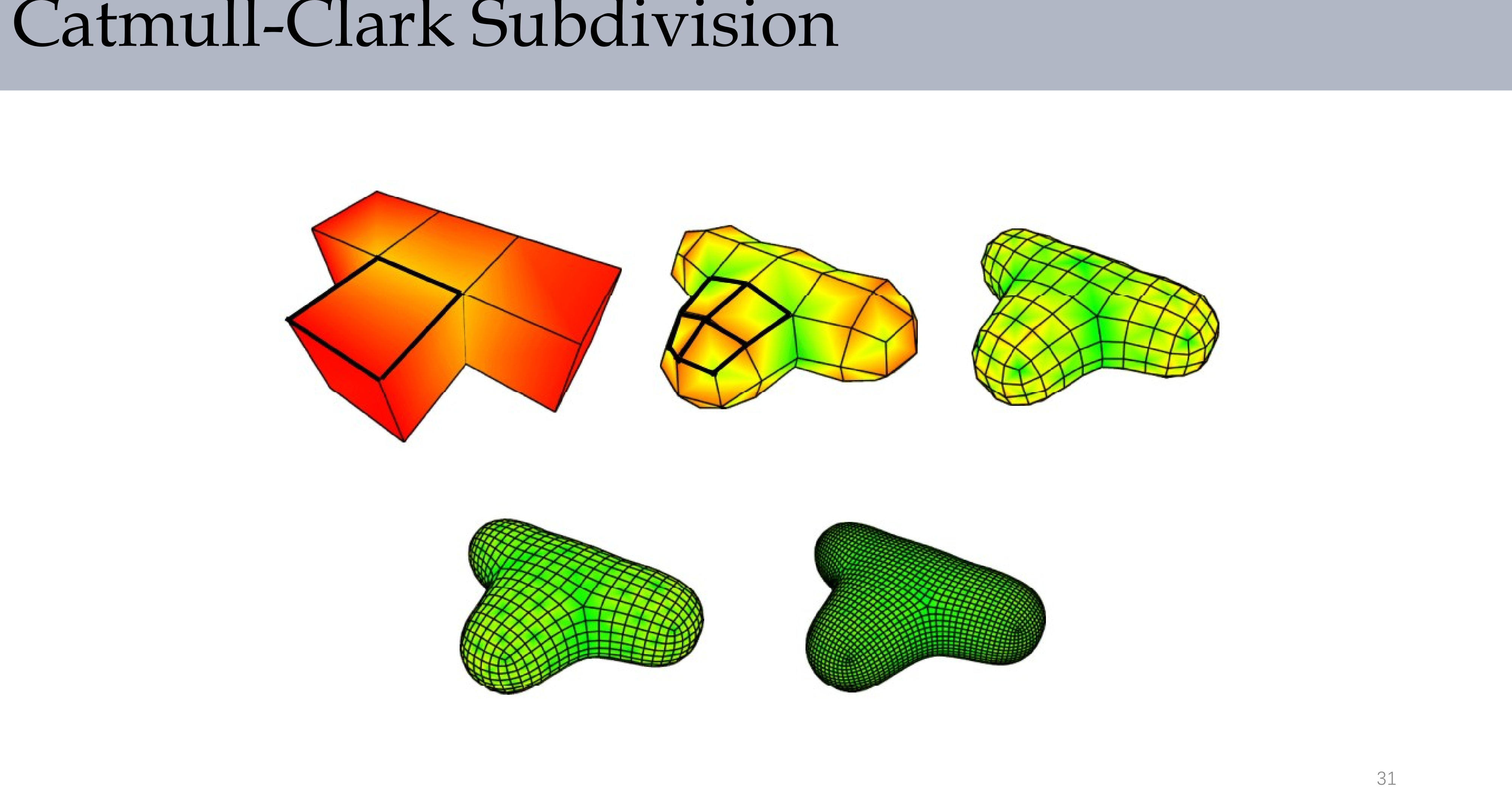
上图展示了从简单的四边形网格经过多次Catmull-Clark细分，最终生成光滑曲面的完整过程。

Loop细分

适用对象： 三角形网格

细分规则：

  1. 添加新顶点（Edge Midpoint）

对于有两个邻接面的边：

\[v_{new} = \frac{3}{8}(v_0 + v_2) + \frac{1}{8}(v_1 + v_3)\]

对于边界边：

\[v_{new} = \frac{v_0 + v_1}{2}\]
  1. 更新旧顶点
\[v' = (1 - n \cdot u)v + \sum_{i=1}^{n} u v_i\]

其中：

  • \(n\)：顶点度数
  • \(u = \frac{3}{16}\)（若\(n=3\)），\(u = \frac{3}{8n}\)（其他情况）

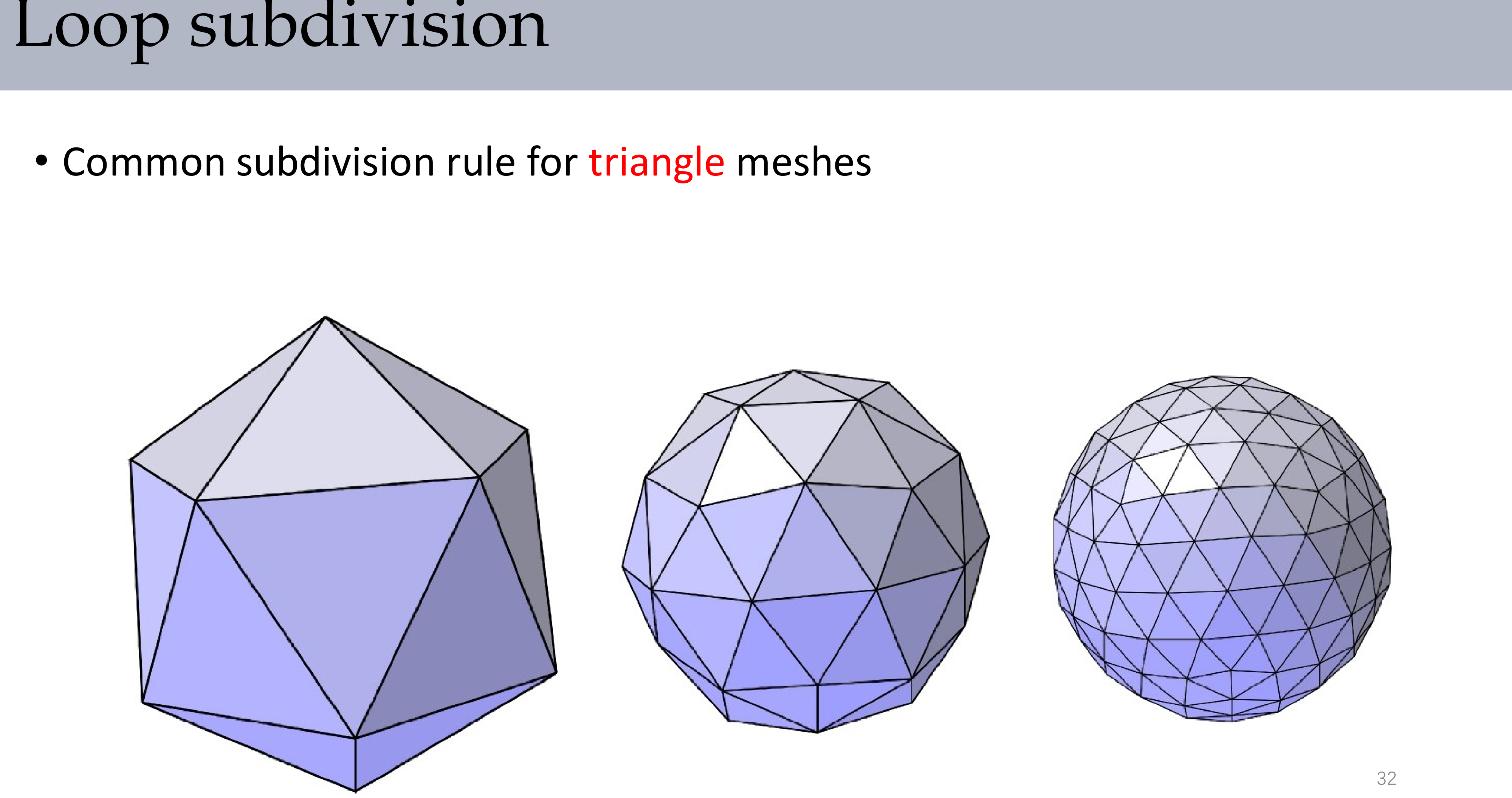
上图展示了二十面体经过Loop细分逐步逼近球面的过程。每次细分将每个三角形分为四个，并更新顶点位置。

细分曲面的优点：

  • 用少量顶点定义光滑曲面
  • 支持任意拓扑
  • 多分辨率表示
  • 易于编辑

网格参数化（Mesh Parameterization）

基本概念

网格参数化 是将三维曲面与二维区域建立一一对应关系的过程。

\[\phi: S \rightarrow \mathbb{R}^2, \quad (x,y,z) \mapsto (u,v)\]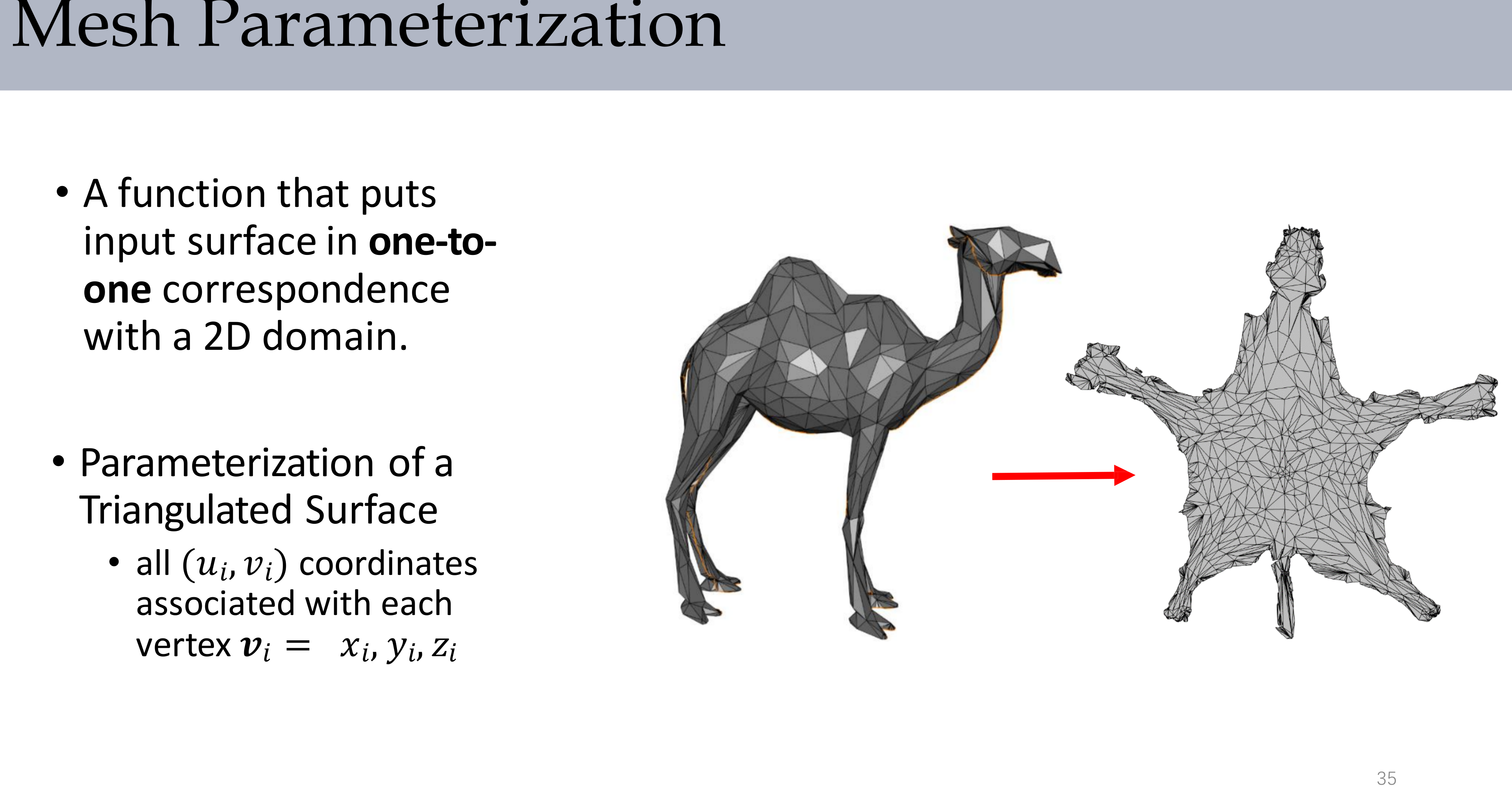

上图展示了将三维骆驼模型展开到二维平面的参数化过程。每个三维顶点对应一个二维坐标\((u_i, v_i)\)。

参数化的应用

1. 纹理映射

将二维纹理图像映射到三维模型表面。

2. 世界地图投影

球面到平面的映射，不同投影方式保留不同性质：

  • 立体投影（Stereographic） - 保角
  • 墨卡托投影（Mercator） - 保角
  • 朗伯投影（Lambert） - 等面积

参数化的几何性质

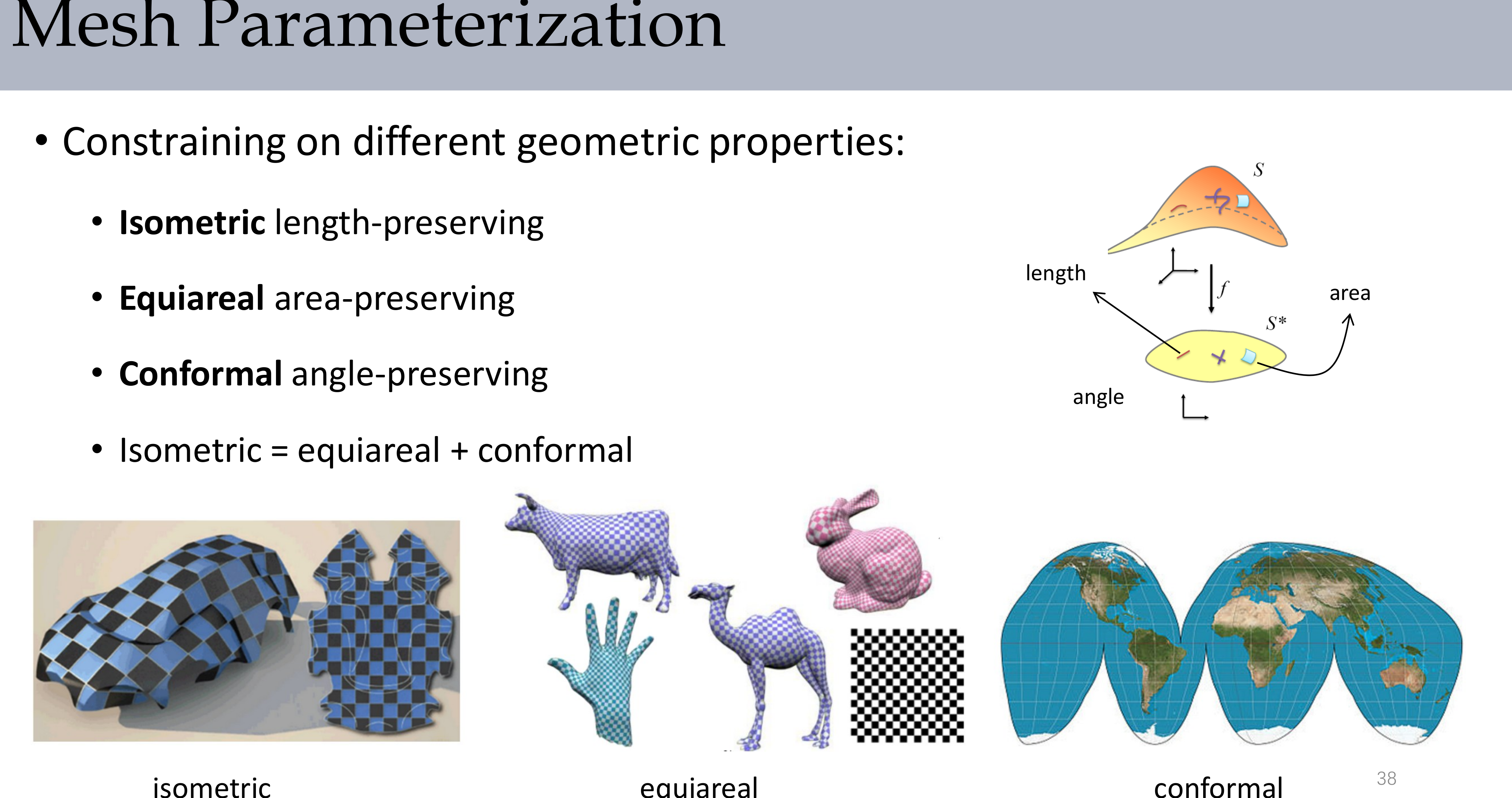
三种重要性质：

  1. 等距（Isometric） - 保持长度
  2. 等面积（Equiareal） - 保持面积
  3. 保角（Conformal） - 保持角度

关系： 等距 = 等面积 + 保角

对于一般曲面，三者不可能同时满足，需要在不同应用中做出权衡。

参数化域类型

常见参数化域：

  • 平面参数化 - 将开放网格映射到平面
  • 球面参数化 - 将闭合网格映射到球面
  • 基域参数化 - 映射到简单的多边形域

平面参数化方法

弹簧系统（Spring System）方法：

能量函数：

\[E = \frac{1}{2}\sum_{i=1}^{n}\sum_{j \in N_i} \frac{1}{2}D_{ij} \|\mathbf{t}_i - \mathbf{t}_j\|^2\]

其中：

  • \(\mathbf{t}_i = (u_i, v_i)\)：顶点的2D参数坐标
  • \(D_{ij}\)：弹簧系数
  • \(N_i\)：顶点\(i\)的邻接顶点集合

最小化条件：

\[\frac{\partial E}{\partial \mathbf{t}_i} = \sum_{j \in N_i} D_{ij}(\mathbf{t}_i - \mathbf{t}_j) = 0\]

线性方程组：

\[\mathbf{t}_i = \sum_{j \in N_i} \lambda_{ij} \mathbf{t}_j\]

其中：

\[\lambda_{ij} = \frac{D_{ij}}{\sum_{k \in N_i} D_{ik}}\]

常用权重：

  1. 均匀权重（Uniform）
\[\lambda_{ij} = \frac{1}{n_i}\]
  1. 调和坐标（Harmonic）
\[\lambda_{ij} = \frac{\cot \gamma_{ij} + \cot \gamma_{ji}}{2}\]
  1. 平均值坐标（Mean Value）
\[\lambda_{ij} = \left(\tan\frac{\alpha_{ij}}{2} + \tan\frac{\beta_{ji}}{2}\right) / r_{ij}\]

边界条件：

  • 固定边界： 将边界顶点固定到规则形状（如圆形或矩形）
  • 自由边界： 同时优化边界和内部顶点

求解： 形成稀疏线性方程组\(\mathbf{A}\mathbf{t} = \mathbf{b}\)，可用直接法或迭代法求解。

可展曲面 vs 一般曲面

可展曲面（Developable Surface）：

  • 可以无失真地展开到平面
  • 例如：圆柱、圆锥、平面
  • 高斯曲率为零

一般曲面：

  • 展开必然产生失真
  • 例如：球面、鞍面
  • 需要在不同性质间权衡

小结

本章介绍了计算机中几何表示的主要方法：

基本表示方法：

  • 点云 - 最简单，来自扫描
  • 多边形网格 - 最常用，易于渲染
  • 三角形网格 - GPU友好，数据结构成熟
  • 四边形网格 - 易于参数化，适合建模

高级数据结构：

  • 半边结构 - 高效查询邻接关系
  • 细分曲面 - 光滑表示，多分辨率

网格参数化：

  • 纹理映射的基础
  • 需要在几何性质间权衡
  • 弹簧系统是经典方法

应用领域：

  • 三维建模与动画
  • 游戏与虚拟现实
  • CAD/CAM
  • 计算机视觉与重建

几何表示是计算机图形学的基础，不同的应用场景需要选择合适的表示方法。



Enjoy Reading This Article?

Here are some more articles you might like to read next:

  • notes of ML
  • notes of VCI
  • notes of AIP
  • notes of AI Math Fundamentals
  • notes of ICS