VCI - 6: 曲线 | STIBIUMS

曲线概述

曲线在计算机图形学中的重要性

曲线是计算机图形学、计算机辅助设计（CAD）、计算机辅助制造（CAM）和计算机辅助工程（CAE）的基础元素。它们不仅用于创建美观的图形，更是精确建模复杂几何形状的核心工具。

应用领域：

工业设计：汽车外形、飞机机翼设计
动画制作：角色轮廓、运动路径
字体设计：字符轮廓和曲线细节
架构建模：建筑曲面和装饰元素
游戏开发：地形、道路和环境元素

曲线的数学基础

曲线的数学表示方法直接影响其在计算机中的处理效率和精度。不同的表示方法适用于不同的应用场景。

二维曲线表示方法

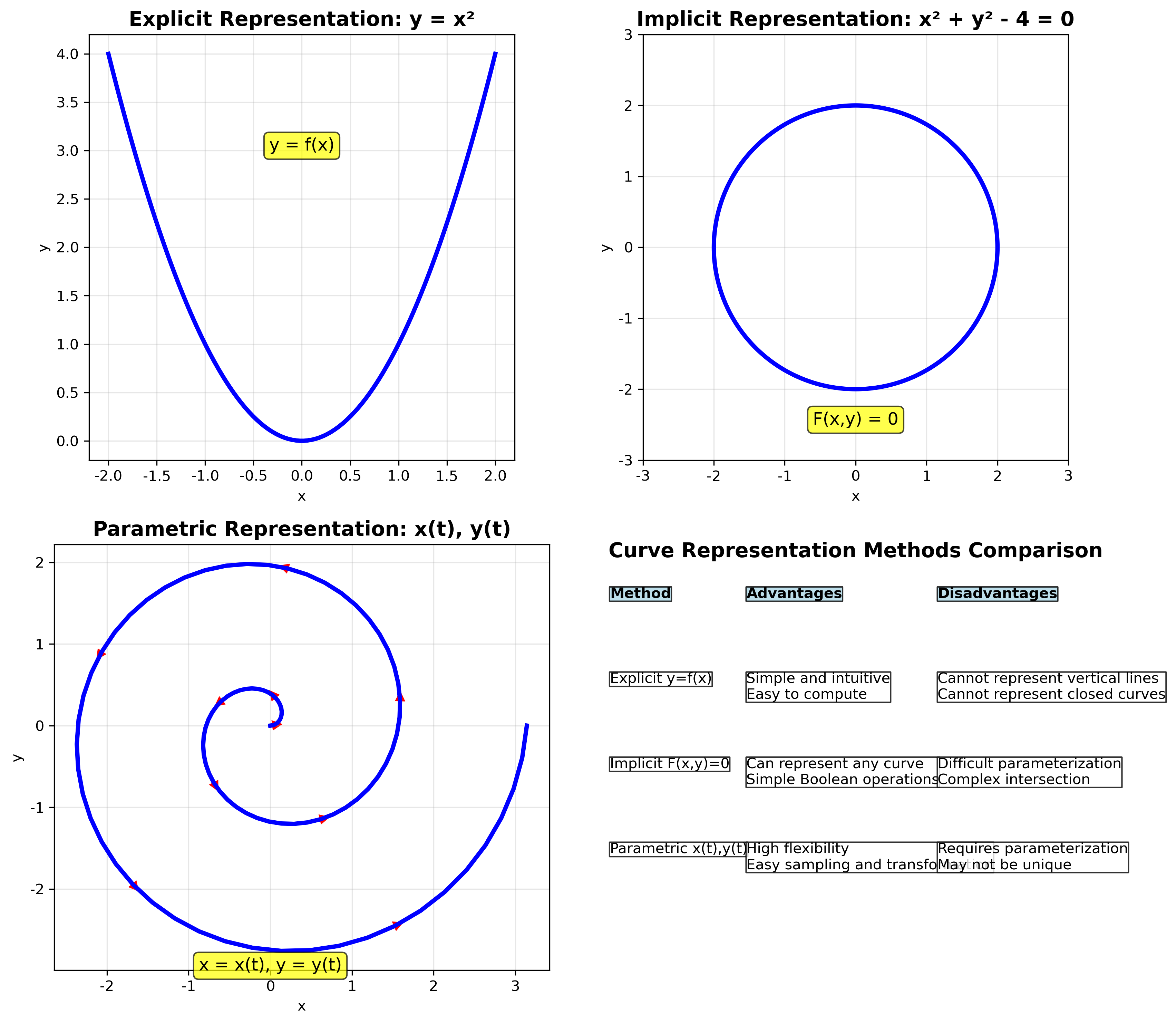
显式表示（Explicit Representation）

定义：将曲线表示为 $y = f(x)$ 的函数形式。

数学形式： $y = f(x), \quad x \in [a, b]$

特点与局限性：

优势：
- 简单直观，易于理解
- 计算导数和积分相对简单
- 适合表示函数图像
局限性：
- 无法表示垂直线（$\frac{dy}{dx} = \infty$）
- 不能表示闭合曲线
- 多值函数需要分段处理
- 旋转和变换操作复杂

典型应用：简单函数曲线、二次函数抛物线

隐式表示（Implicit Representation）

定义：将曲线定义为方程 $F(x,y) = 0$ 的解集。

数学形式： $F(x,y) = 0$

常见隐式曲线：

圆：$x^2 + y^2 - r^2 = 0$
椭圆：$\frac{x^2}{a^2} + \frac{y^2}{b^2} - 1 = 0$
双曲线：$\frac{x^2}{a^2} - \frac{y^2}{b^2} - 1 = 0$

特点分析：

优势：
- 可以表示任意方向的曲线
- 自然处理闭合曲线和多重连通区域
- 布尔运算（并、交、差）操作简单
- 曲线内外判断直接：$F(x,y) > 0$（外部）或 $F(x,y) < 0$（内部）
局限性：
- 参数化困难，难以进行曲线上的均匀采样
- 求交点和计算曲线长度复杂
- 不适合动画中的路径跟踪
- 高次方程求解困难

参数表示（Parametric Representation）

定义：使用参数 $t$ 来表示曲线上的点。

数学形式：

\[\begin{cases} x = x(t) \\ y = y(t) \end{cases} \quad t \in [t_0, t_1]\]

向量表示： $\mathbf{C}(t) = [x(t), y(t)]^T$

参数曲线的优势：

方向性：参数 $t$ 增加的方向定义了曲线的正方向
灵活性：可以表示任意复杂的曲线形状
易于采样：通过改变 $t$ 值均匀地在曲线上采样
变换简单：几何变换直接应用于参数方程
动画友好：$t$ 可以直接表示时间参数

参数化的非唯一性：

同一条曲线可以有多种参数化方式：

标准参数化：$t \in [0,1]$
弧长参数化：$t$ 表示从起点的弧长
速度参数化：$t$ 与运动速度相关

曲线表示方法对比：左上为显式表示y=f(x)，右上为隐式表示F(x,y)=0，左下为参数表示x(t),y(t)，右下为三种方法的优缺点对比表

贝塞尔曲线（Bézier Curves）

贝塞尔曲线的发展历史

贝塞尔曲线由法国工程师皮埃尔·贝塞尔（Pierre Bézier）在1960年代为雷诺汽车公司开发，用于汽车车身的数字化设计。这一创新性工作奠定了现代CAD/CAM系统的基础。

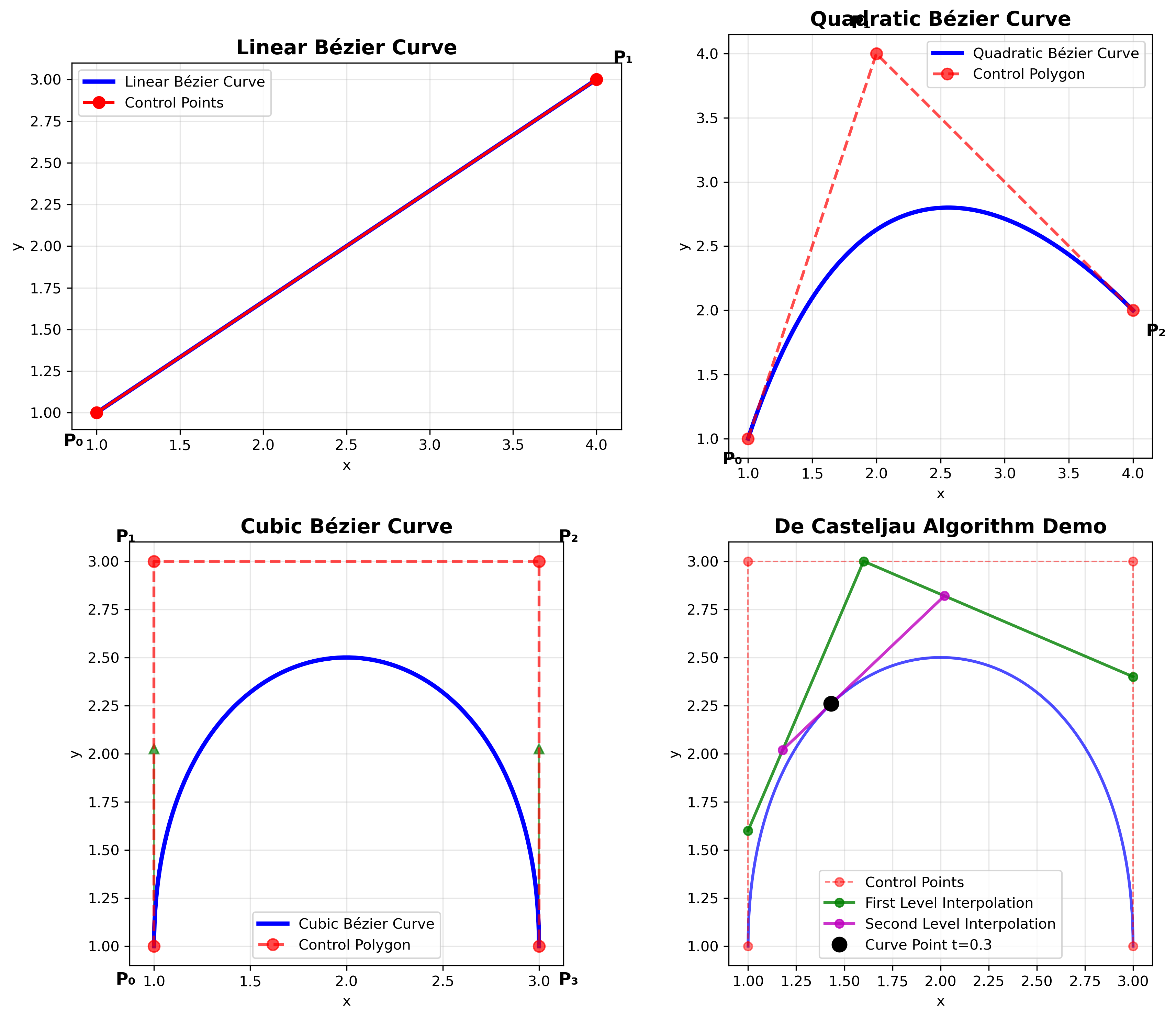
线性贝塞尔曲线

定义：连接两个控制点的直线段。

\[\mathbf{B}(t) = (1-t)\mathbf{P}_0 + t\mathbf{P}_1, \quad t \in [0,1]\]

几何解释：

当 $t = 0$ 时，$\mathbf{B}(0) = \mathbf{P}_0$
当 $t = 1$ 时，$\mathbf{B}(1) = \mathbf{P}_1$
$t$ 表示从 $\mathbf{P}_0$ 到 $\mathbf{P}_1$ 的插值比例

二次贝塞尔曲线

定义：由三个控制点定义的二次曲线。

\[\mathbf{B}(t) = (1-t)^2\mathbf{P}_0 + 2t(1-t)\mathbf{P}_1 + t^2\mathbf{P}_2\]

递归构造（De Casteljau算法）：

第一层插值： $\mathbf{Q}_0(t) = (1-t)\mathbf{P}_0 + t\mathbf{P}_1$ $\mathbf{Q}_1(t) = (1-t)\mathbf{P}_1 + t\mathbf{P}_2$
第二层插值： $\mathbf{B}(t) = (1-t)\mathbf{Q}_0(t) + t\mathbf{Q}_1(t)$

几何特性：

端点插值：曲线通过 $\mathbf{P}_0$ 和 $\mathbf{P}_2$
切线性质：在 $\mathbf{P}_0$ 处的切线方向为 $\mathbf{P}_1 - \mathbf{P}_0$
对称性：关于参数 $t = 0.5$ 对称

三次贝塞尔曲线

定义：计算机图形学中最常用的贝塞尔曲线类型。

\[\mathbf{B}(t) = (1-t)^3\mathbf{P}_0 + 3t(1-t)^2\mathbf{P}_1 + 3t^2(1-t)\mathbf{P}_2 + t^3\mathbf{P}_3\]

矩阵形式：

\[\mathbf{B}(t) = \begin{bmatrix} 1 & t & t^2 & t^3 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ -3 & 3 & 0 & 0 \\ 3 & -6 & 3 & 0 \\ -1 & 3 & -3 & 1 \end{bmatrix} \begin{bmatrix} \mathbf{P}_0 \\ \mathbf{P}_1 \\ \mathbf{P}_2 \\ \mathbf{P}_3 \end{bmatrix}\]

切线向量：

起点切线：$\mathbf{B}’(0) = 3(\mathbf{P}_1 - \mathbf{P}_0)$
终点切线：$\mathbf{B}’(1) = 3(\mathbf{P}_3 - \mathbf{P}_2)$

一般n次贝塞尔曲线

Bernstein基函数定义：

\[\mathbf{B}(t) = \sum_{i=0}^{n} \mathbf{P}_i B_{i,n}(t)\]

其中Bernstein基函数为：

\[B_{i,n}(t) = \binom{n}{i} t^i (1-t)^{n-i}\]

Bernstein基函数的性质：

非负性：$B_{i,n}(t) \geq 0$ 对所有 $t \in [0,1]$
单位分割：$\sum_{i=0}^{n} B_{i,n}(t) = 1$
端点性质：
- $B_{i,n}(0) = \delta_{i,0}$（Kronecker delta）
- $B_{i,n}(1) = \delta_{i,n}$
对称性：$B_{i,n}(t) = B_{n-i,n}(1-t)$

De Casteljau算法

算法原理：通过递归线性插值计算贝塞尔曲线上的点。

算法步骤：

对于n次贝塞尔曲线，定义：

\[\mathbf{P}_i^{(0)} = \mathbf{P}_i, \quad i = 0, 1, \ldots, n\] \[\mathbf{P}_i^{(k)} = (1-t)\mathbf{P}_i^{(k-1)} + t\mathbf{P}_{i+1}^{(k-1)}, \quad k = 1, 2, \ldots, n\]

最终结果：$\mathbf{B}(t) = \mathbf{P}_0^{(n)}$

算法优势：

数值稳定性：避免了高次幂计算
几何直观性：每一步都有明确的几何意义
细分友好：可以同时获得曲线细分结果

贝塞尔曲线的几何性质

端点插值性

贝塞尔曲线通过其首末控制点：

$\mathbf{B}(0) = \mathbf{P}_0$
$\mathbf{B}(1) = \mathbf{P}_n$

切线性质

曲线在端点的切线由相邻控制点确定：

起点切线：$\mathbf{B}’(0) \propto (\mathbf{P}_1 - \mathbf{P}_0)$
终点切线：$\mathbf{B}’(1) \propto (\mathbf{P}n - \mathbf{P}{n-1})$

凸包性质

定理：贝塞尔曲线完全位于其控制点构成的凸包内。

证明要点：由于Bernstein基函数的非负性和单位分割性质，曲线上的任意点都是控制点的凸组合。

实际意义：

曲线不会偏离控制多边形太远
提供了曲线的边界估计
有利于碰撞检测和裁剪算法

仿射不变性

贝塞尔曲线在仿射变换下保持形状特征：

\[T(\mathbf{B}(t)) = \sum_{i=0}^{n} T(\mathbf{P}_i) B_{i,n}(t)\]

支持的变换：

平移、旋转、缩放
剪切变换
透视投影（需要有理贝塞尔曲线）

变差递减性质

定理：与贝塞尔曲线相交的直线数目不超过与其控制多边形相交的直线数目。

几何意义：

贝塞尔曲线比控制多边形”更平滑”
曲线不会产生比控制多边形更多的振荡
保证了曲线的稳定性和可预测性

贝塞尔曲线演示：左上为线性贝塞尔曲线，右上为二次贝塞尔曲线，左下为三次贝塞尔曲线及其切线，右下为De Casteljau算法的几何构造过程

贝塞尔曲线的拼接

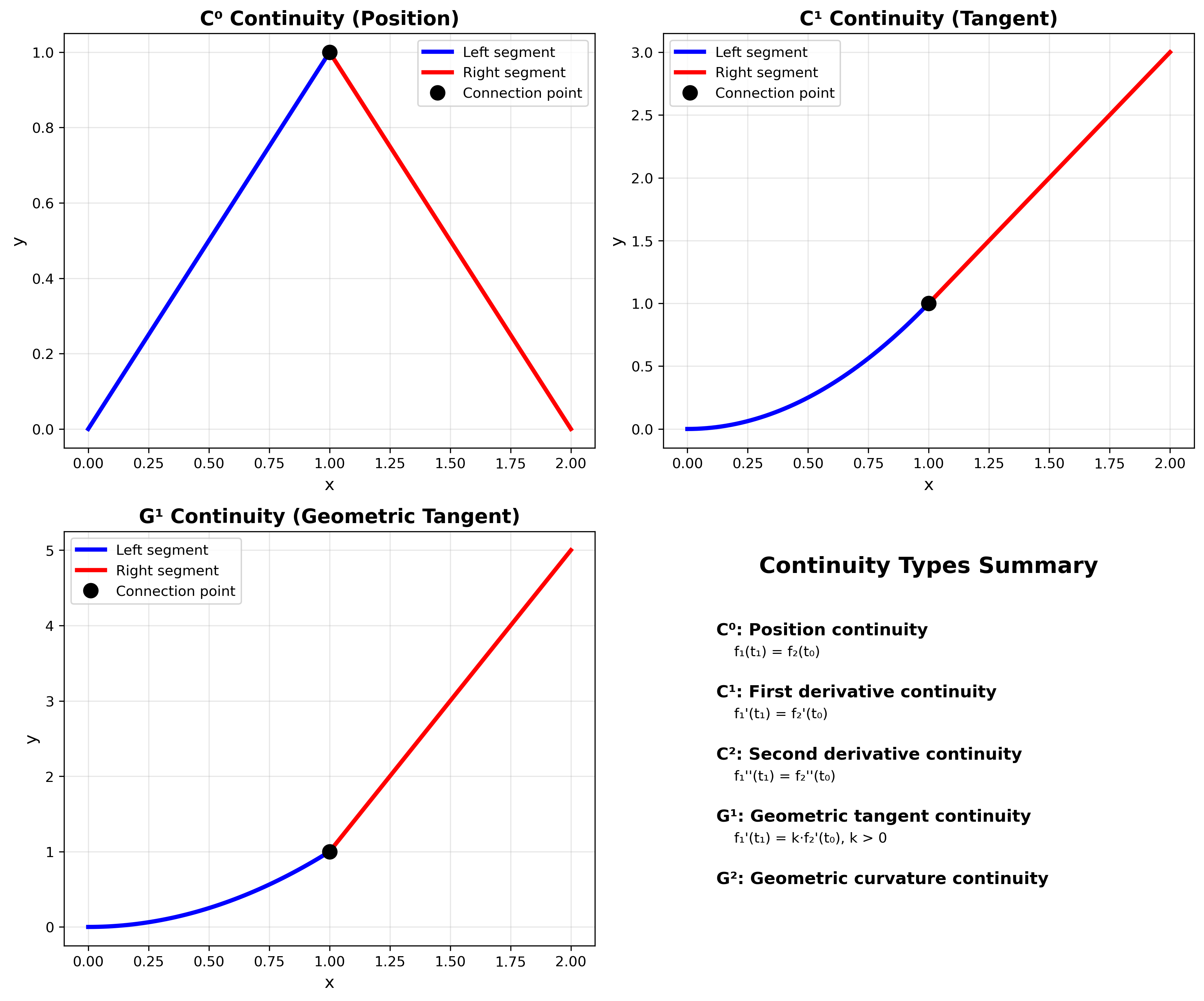
C⁰连续性（位置连续）

两条贝塞尔曲线 $\mathbf{B}_1(t)$ 和 $\mathbf{B}_2(t)$ 满足C⁰连续的条件：

\[\mathbf{B}_1(1) = \mathbf{B}_2(0)\]

即第一条曲线的终点与第二条曲线的起点重合。

C¹连续性（切线连续）

除了位置连续外，还需要切线方向连续：

\[\mathbf{B}_1'(1) = \mathbf{B}_2'(0)\]

对于三次贝塞尔曲线，这意味着：

\[3(\mathbf{P}_{1,3} - \mathbf{P}_{1,2}) = 3(\mathbf{P}_{2,1} - \mathbf{P}_{2,0})\]

C²连续性（曲率连续）

进一步要求二阶导数连续：

\[\mathbf{B}_1''(1) = \mathbf{B}_2''(0)\]

G连续性（几何连续性）

G⁰：位置连续（同C⁰）
G¹：切线方向连续（允许切线长度不同）
G²：曲率连续

G连续性比C连续性要求更宽松，在实际应用中更为实用。

左图：不同连续性类型的对比演示，包括C⁰、C¹、G¹连续性的几何意义；右图：不同样条类型的对比，展示自然三次样条、夹紧样条和线性插值的差异

样条曲线（Spline Curves）

样条曲线的历史背景

样条（Spline）一词来源于造船业，指用于绘制船体曲线的柔性木条或金属条。数学上的样条曲线继承了这一思想：通过分段多项式函数构造光滑曲线。

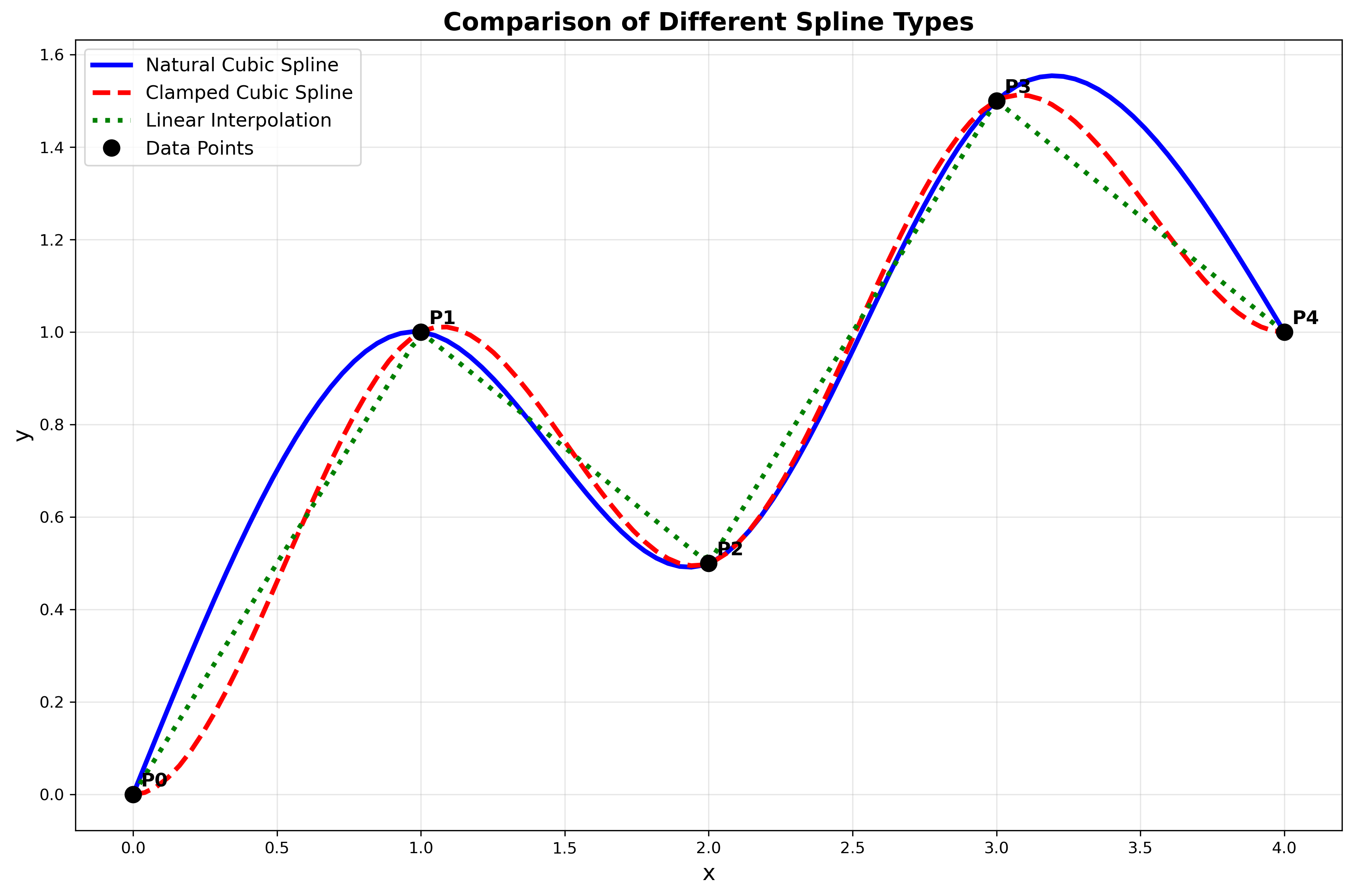
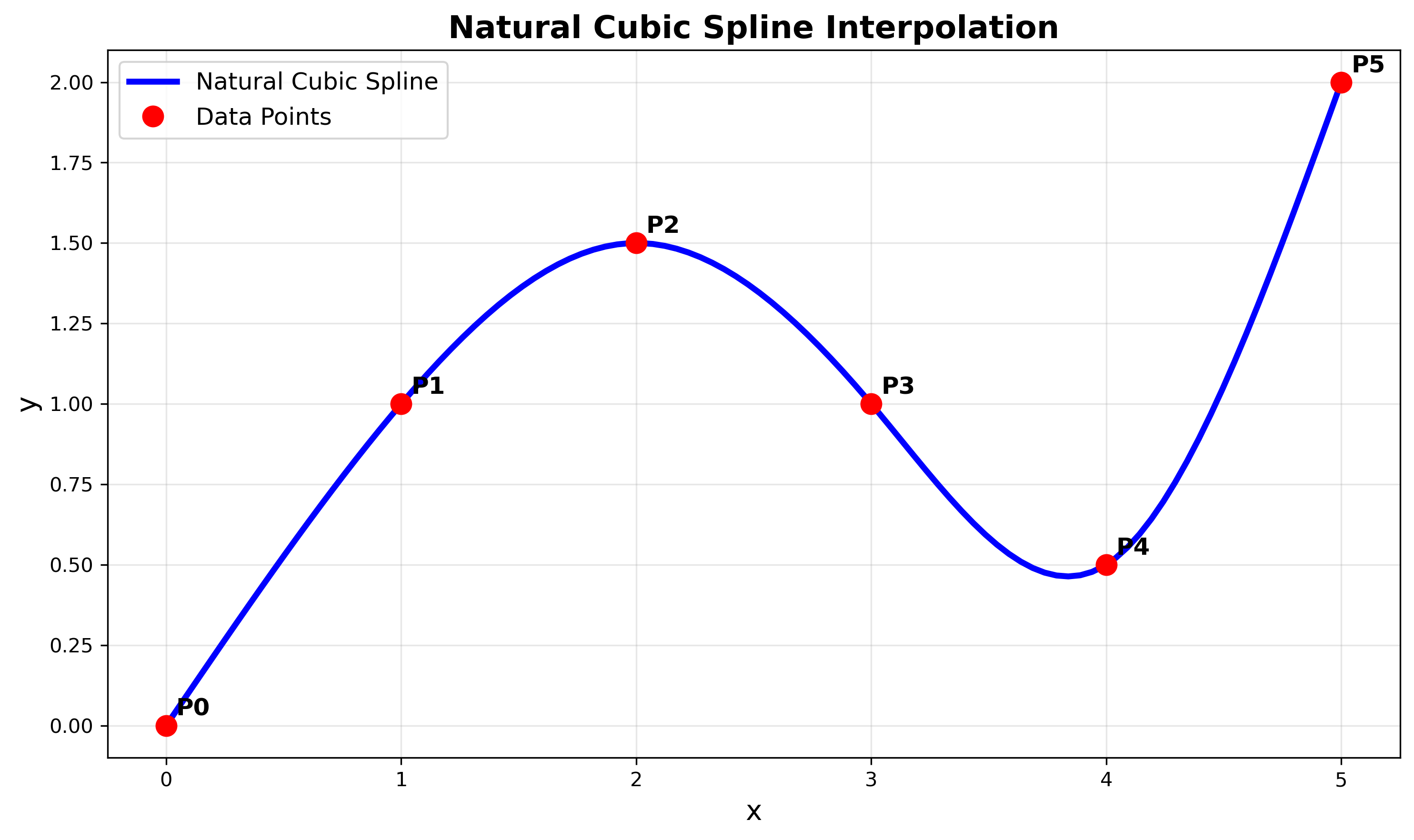
三次自然样条（Natural Cubic Spline）

数学定义

给定数据点 $(x_0, y_0), (x_1, y_1), \ldots, (x_n, y_n)$，构造分段三次多项式：

\[S(x) = S_i(x) = a_i + b_i(x - x_i) + c_i(x - x_i)^2 + d_i(x - x_i)^3\]

对于 $x \in [x_i, x_{i+1}]$，$i = 0, 1, \ldots, n-1$。

连续性约束

C⁰连续性： $S_i(x_{i+1}) = S_{i+1}(x_{i+1}), \quad i = 0, 1, \ldots, n-2$

C¹连续性： $S_i'(x_{i+1}) = S_{i+1}'(x_{i+1}), \quad i = 0, 1, \ldots, n-2$

C²连续性： $S_i''(x_{i+1}) = S_{i+1}''(x_{i+1}), \quad i = 0, 1, \ldots, n-2$

自然边界条件

\[S''(x_0) = S''(x_n) = 0\]

这意味着样条在端点处的曲率为零，类似于自由端的物理样条。

求解方法

设 $M_i = S’‘(x_i)$，则可以推导出三对角线性方程组：

\[\begin{bmatrix} 2(h_0 + h_1) & h_1 & 0 & \cdots & 0 \\ h_1 & 2(h_1 + h_2) & h_2 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & h_{n-2} & 2(h_{n-2} + h_{n-1}) \end{bmatrix} \begin{bmatrix} M_1 \\ M_2 \\ \vdots \\ M_{n-1} \end{bmatrix} = \begin{bmatrix} 6f[x_0, x_1, x_2] \\ 6f[x_1, x_2, x_3] \\ \vdots \\ 6f[x_{n-2}, x_{n-1}, x_n] \end{bmatrix}\]

其中 $h_i = x_{i+1} - x_i$，$f[x_i, x_{j}, x_k]$ 是二阶差商。

自然三次样条插值演示：蓝色曲线为插值结果，红色点为给定的数据点，样条在端点处的二阶导数为零

Hermite样条

Hermite样条不仅插值数据点，还插值给定的导数值。

三次Hermite插值

给定端点 $(x_0, y_0, y_0’)$ 和 $(x_1, y_1, y_1’)$，构造三次多项式：

\[H(t) = y_0 H_0(t) + y_1 H_1(t) + y_0' H_2(t) + y_1' H_3(t)\]

其中Hermite基函数为：

\[\begin{align} H_0(t) &= (1 + 2t)(1 - t)^2 \\ H_1(t) &= t^2(3 - 2t) \\ H_2(t) &= t(1 - t)^2 \\ H_3(t) &= t^2(t - 1) \end{align}\]

Cardinal样条

Cardinal样条是Hermite样条的特例，导数值通过相邻点自动确定：

\[y_i' = \frac{1 - c}{2}(y_{i+1} - y_{i-1})\]

其中 $c$ 是张力参数（tension parameter）：

$c = 0$：Catmull-Rom样条
$c = 1$：线性插值

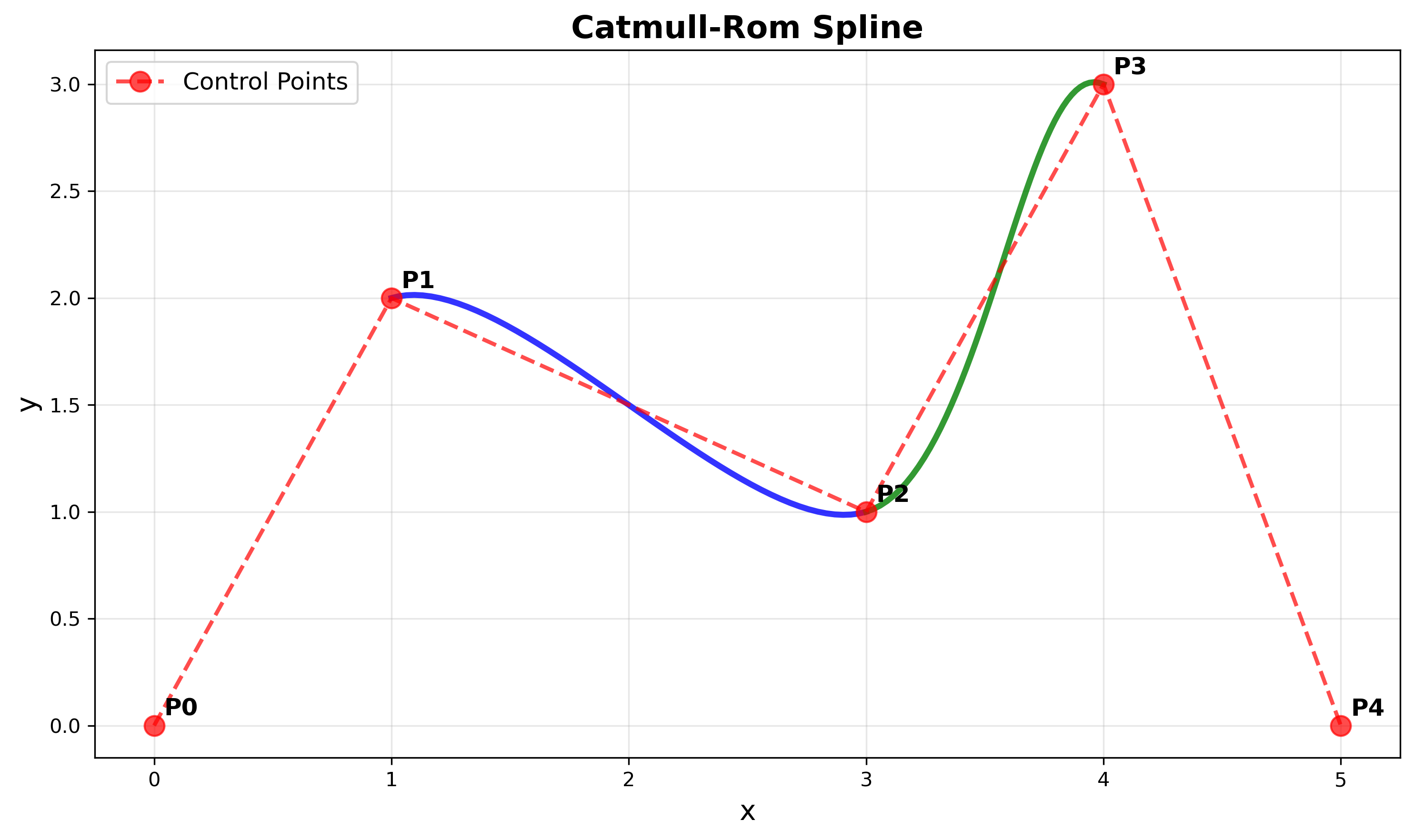
Catmull-Rom样条

Catmull-Rom样条是最常用的插值样条之一，特别适合关键帧动画。

数学表达

对于四个连续控制点 $\mathbf{P}_0, \mathbf{P}_1, \mathbf{P}_2, \mathbf{P}_3$，在区间 $[\mathbf{P}_1, \mathbf{P}_2]$ 上的Catmull-Rom样条为：

\[\mathbf{C}(t) = \frac{1}{2} \begin{bmatrix} 1 & t & t^2 & t^3 \end{bmatrix} \begin{bmatrix} 0 & 2 & 0 & 0 \\ -1 & 0 & 1 & 0 \\ 2 & -5 & 4 & -1 \\ -1 & 3 & -3 & 1 \end{bmatrix} \begin{bmatrix} \mathbf{P}_0 \\ \mathbf{P}_1 \\ \mathbf{P}_2 \\ \mathbf{P}_3 \end{bmatrix}\]

特性

插值性：曲线通过 $\mathbf{P}_1$ 和 $\mathbf{P}_2$
C¹连续性：相邻段之间切线连续
局部控制：每段曲线只受四个控制点影响
切线自动计算：不需要手动指定切线方向

Catmull-Rom样条演示：不同颜色的曲线段展示了多段样条的连接，红色虚线显示控制多边形，每段曲线由四个连续控制点确定

B样条曲线（B-Spline Curves）

B样条的发展

B样条（Basis Spline）由Carl de Boor和其他数学家在1970年代发展完善，克服了贝塞尔曲线在处理大量控制点时的局限性。

均匀B样条

基函数定义

B样条基函数通过Cox-de Boor递归公式定义：

0次基函数：

\[N_{i,0}(t) = \begin{cases} 1, & t_i \leq t < t_{i+1} \\ 0, & \text{otherwise} \end{cases}\]

递归定义： $N_{i,k}(t) = \frac{t - t_i}{t_{i+k} - t_i} N_{i,k-1}(t) + \frac{t_{i+k+1} - t}{t_{i+k+1} - t_{i+1}} N_{i+1,k-1}(t)$

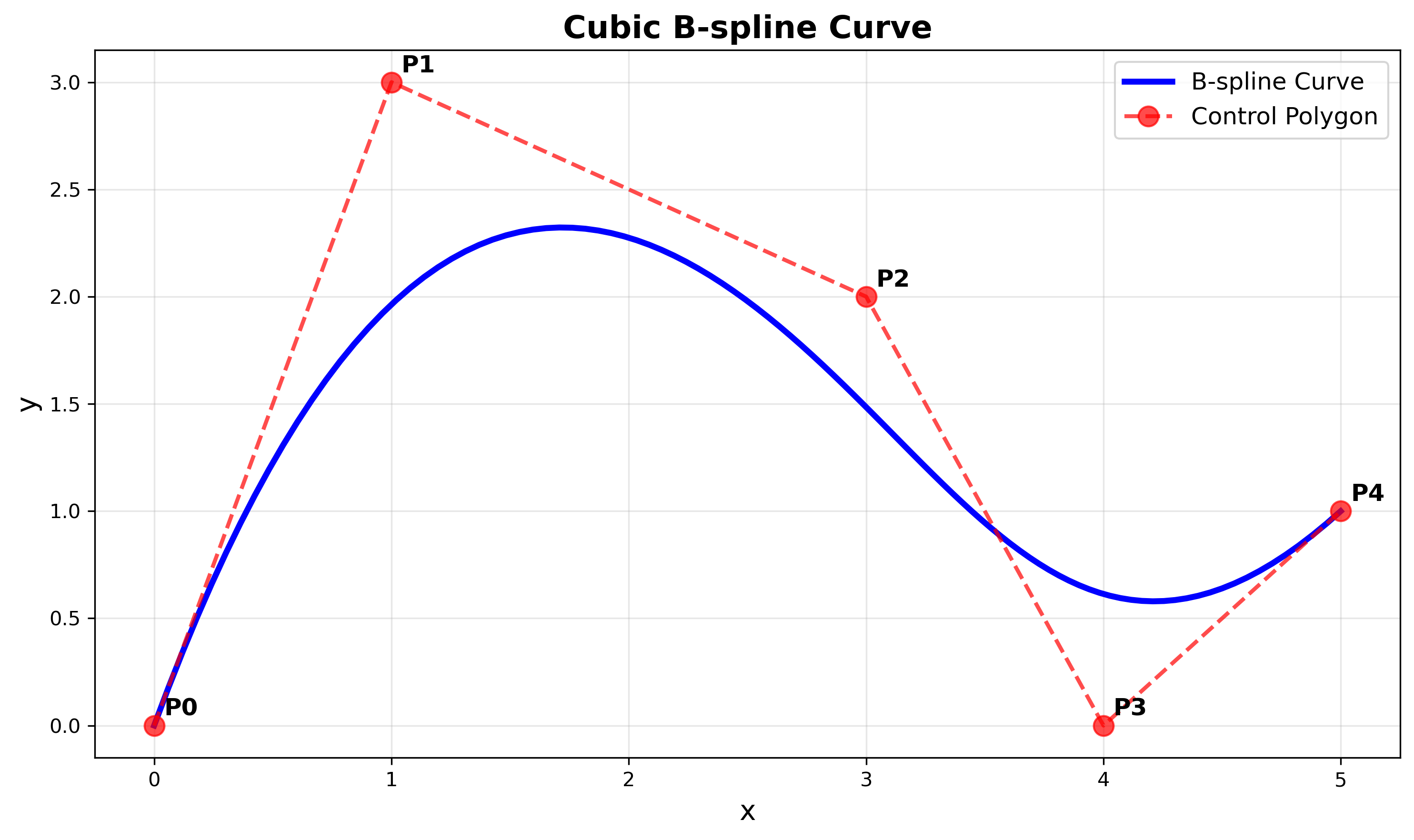
B样条曲线

k次B样条曲线定义为：

\[\mathbf{C}(t) = \sum_{i=0}^{n} \mathbf{P}_i N_{i,k}(t)\]

其中 $\mathbf{P}i$ 是控制点，$N{i,k}(t)$ 是k次B样条基函数。

节点向量（Knot Vector）

节点向量 $\mathbf{T} = [t_0, t_1, \ldots, t_m]$ 定义了参数域的分割：

均匀节点向量：节点等间距分布
非均匀节点向量：节点间距可以不等
重复节点：允许相同的节点值

开放均匀节点向量

对于n+1个控制点和k次B样条：

\[\mathbf{T} = [\underbrace{0, \ldots, 0}_{k+1}, \frac{1}{n-k+1}, \frac{2}{n-k+1}, \ldots, \frac{n-k}{n-k+1}, \underbrace{1, \ldots, 1}_{k+1}]\]

特点：

曲线通过首末控制点
端点处具有k重节点
适合开放曲线

周期均匀节点向量

\[\mathbf{T} = [0, 1, 2, \ldots, n+k+1]\]

特点：

所有节点间距相等
适合封闭曲线
具有周期性

B样条的性质

局部支撑性

k次B样条基函数 $N_{i,k}(t)$ 只在区间 $[t_i, t_{i+k+1}]$ 上非零。

实际意义：

移动一个控制点只影响k+1段曲线
比贝塞尔曲线具有更好的局部控制性
适合交互式设计

凸包性质

曲线位于当前”活跃”控制点的凸包内。

变差递减性质

与贝塞尔曲线类似，B样条曲线也满足变差递减性质。

仿射不变性

B样条曲线在仿射变换下保持其基本性质。

三次B样条曲线演示：蓝色实线为B样条曲线，红色虚线为控制多边形，展示了B样条的局部控制特性和平滑性

非均匀B样条

节点插入

在现有节点向量中插入新节点，不改变曲线形状，但增加控制点数量。

算法：给定节点 $\bar{t}$ 插入到区间 $[t_j, t_{j+1}]$：

\[\bar{\mathbf{P}}_i = \begin{cases} \mathbf{P}_i, & i \leq j - k \\ \alpha_i \mathbf{P}_i + (1 - \alpha_i) \mathbf{P}_{i-1}, & j - k + 1 \leq i \leq j \\ \mathbf{P}_{i-1}, & i \geq j + 1 \end{cases}\]

其中 $\alpha_i = \frac{\bar{t} - t_i}{t_{i+k} - t_i}$。

节点移除

移除不必要的节点以简化曲线表示，同时保持形状精度。

B样条曲线的微分

导数计算

k次B样条曲线的导数是k-1次B样条曲线：

\[\mathbf{C}'(t) = \sum_{i=0}^{n-1} \mathbf{Q}_i N_{i,k-1}(t)\]

其中： $\mathbf{Q}_i = \frac{k}{t_{i+k+1} - t_{i+1}} (\mathbf{P}_{i+1} - \mathbf{P}_i)$

B样条曲面

B样条可以扩展到曲面：

\[\mathbf{S}(u,v) = \sum_{i=0}^{m} \sum_{j=0}^{n} \mathbf{P}_{i,j} N_{i,p}(u) N_{j,q}(v)\]

其中 $N_{i,p}(u)$ 和 $N_{j,q}(v)$ 分别是u方向和v方向的B样条基函数。

NURBS曲线

NURBS简介

NURBS（Non-Uniform Rational B-Splines，非均匀有理B样条）是B样条的有理扩展，是现代CAD/CAM系统的标准曲线表示方法。

有理贝塞尔曲线

定义：在贝塞尔曲线的基础上为每个控制点添加权重：

\[\mathbf{R}(t) = \frac{\sum_{i=0}^{n} w_i \mathbf{P}_i B_{i,n}(t)}{\sum_{i=0}^{n} w_i B_{i,n}(t)}\]

其中 $w_i$ 是第i个控制点的权重。

齐次坐标表示：

\[\mathbf{P}_i^w = [w_i x_i, w_i y_i, w_i z_i, w_i]^T\] \[\mathbf{R}^w(t) = \sum_{i=0}^{n} \mathbf{P}_i^w B_{i,n}(t)\]

通过透视除法得到：

\[\mathbf{R}(t) = \frac{[\mathbf{R}^w(t)]_{xyz}}{[\mathbf{R}^w(t)]_w}\]

NURBS曲线定义

k次NURBS曲线定义为：

\[\mathbf{C}(t) = \frac{\sum_{i=0}^{n} w_i \mathbf{P}_i N_{i,k}(t)}{\sum_{i=0}^{n} w_i N_{i,k}(t)}\]

定义有理基函数：

\[R_{i,k}(t) = \frac{w_i N_{i,k}(t)}{\sum_{j=0}^{n} w_j N_{j,k}(t)}\]

则NURBS曲线简化为：

\[\mathbf{C}(t) = \sum_{i=0}^{n} \mathbf{P}_i R_{i,k}(t)\]

NURBS的优势

精确表示圆锥曲线

NURBS可以精确表示圆、椭圆、抛物线、双曲线等解析曲线。

圆的NURBS表示：

使用9个控制点和权重可以精确表示完整圆：

$w_0 = w_2 = w_4 = w_6 = w_8 = 1$ $w_1 = w_3 = w_5 = w_7 = \frac{1}{\sqrt{2}}$

透视不变性

NURBS曲线在透视投影下保持其NURBS性质，这对于计算机图形学至关重要。

统一表示

NURBS统一了多项式曲线和有理曲线的表示方法：

当所有权重相等时，NURBS退化为B样条
特殊权重选择可以得到贝塞尔曲线

权重的几何意义

权重增加的效果

增加控制点的权重会将曲线”拉向”该控制点：

$w_i > 1$：曲线更接近 $\mathbf{P}_i$
$w_i < 1$：曲线远离 $\mathbf{P}_i$
$w_i = 0$：$\mathbf{P}_i$ 对曲线无影响

极限情况

$w_i \to \infty$：曲线通过 $\mathbf{P}_i$
$w_i \to 0$：$\mathbf{P}_i$ 的影响消失

NURBS的操作

权重调整

通过调整权重可以改变曲线形状而无需移动控制点，这在设计中非常有用。

节点插入和移除

NURBS继承了B样条的节点操作能力，但需要同时处理权重。

曲线拼接

NURBS曲线的拼接需要考虑权重的连续性，通常要求：

C⁰连续：位置连续
G¹连续：切线方向连续（权重可以不同）
C¹连续：切线向量完全相同

曲线的几何连续性

连续性的分类

参数连续性（C^n连续性）

C⁰连续性：位置连续 $\mathbf{C}_1(1) = \mathbf{C}_2(0)$

C¹连续性：一阶导数连续 $\mathbf{C}_1'(1) = \mathbf{C}_2'(0)$

C²连续性：二阶导数连续 $\mathbf{C}_1''(1) = \mathbf{C}_2''(0)$

几何连续性（G^n连续性）

G⁰连续性：等价于C⁰连续性

G¹连续性：切线方向连续 $\mathbf{C}_1'(1) = k \mathbf{C}_2'(0), \quad k > 0$

G²连续性：曲率连续需要考虑曲率向量的连续性，比C²连续性要求更宽松。

连续性的实际意义

视觉质量

G⁰连续：无明显断裂
G¹连续：无尖角，看起来平滑
G²连续：曲率连续，完全平滑

制造要求

在工业设计中：

Class A曲面：要求G²连续
机械零件：通常G¹连续足够
概念设计：G⁰连续即可

曲线评估与应用

曲线质量评估

曲率分析

曲率公式： $\kappa(t) = \frac{|\mathbf{C}'(t) \times \mathbf{C}''(t)|}{|\mathbf{C}'(t)|^3}$

曲率梳（Curvature Comb）：

在曲线法向绘制与曲率成比例的线段
直观显示曲线的平滑性
用于检测曲率突变

公差分析

弦高误差：近似曲线与原始曲线的最大距离 角度偏差：切线方向的最大偏差

曲线在CAD/CAM中的应用

汽车工业

外形设计：车身轮廓线使用NURBS曲线
Class A曲面：要求极高的连续性和美观性
工具路径：数控加工的刀具路径

航空航天

机翼设计：翼型曲线设计
流线分析：气动特性优化
结构设计：复杂几何形状建模

建筑设计

自由曲面：现代建筑的复杂外形
参数化设计：通过参数控制建筑形态
结构分析：曲线结构的受力分析

动画中的曲线应用

关键帧动画

Catmull-Rom样条：插值关键帧
贝塞尔曲线：手动控制动画曲线
B样条：复杂运动路径

摄像机路径

平滑运动：避免摄像机运动的突变
速度控制：通过重新参数化控制运动速度
取向控制：同时控制位置和朝向

变形动画

形状插值：在不同形状间平滑过渡
骨骼动画：关节旋转的平滑插值
面部动画：表情的自然过渡

计算几何中的曲线算法

曲线求交

参数曲线求交

数值方法：

Newton-Raphson迭代
二分法细分
区间算法

几何方法：

包围盒预筛选
细分求交
平面扫描算法

曲线-直线求交

利用曲线的凸包性质进行快速筛选，然后使用数值方法精确求解。

曲线拟合

插值问题

给定数据点，构造通过所有数据点的曲线：

拉格朗日插值
牛顿插值
样条插值

逼近问题

构造”最佳”近似曲线：

最小二乘法
Chebyshev逼近
约束优化

曲线细分

自适应细分

根据曲率变化自适应地选择细分密度：

function adaptive_subdivision(curve, tolerance):
    if curve_is_flat_enough(curve, tolerance):
        return [curve.start, curve.end]
    else:
        left, right = subdivide_curve(curve, 0.5)
        left_points = adaptive_subdivision(left, tolerance)
        right_points = adaptive_subdivision(right, tolerance)
        return left_points + right_points[1:]  // 避免重复中点

均匀细分

按固定步长进行参数采样，适用于实时渲染。

现代发展趋势

等几何分析

将NURBS等曲线表示直接用于有限元分析，避免了几何转换的误差。

细分曲面

结合多边形建模和NURBS建模的优势，支持任意拓扑结构。

参数化设计

通过高级参数控制曲线族的生成，支持设计优化和自动化。

神经网络方法

使用深度学习方法学习曲线的生成和优化，在某些特定领域显示出潜力。

本笔记基于北京大学视觉计算实验室陈宝权教授的VCI课程内容整理