VCI - 5: 抗锯齿 | STIBIUMS

信号处理基础

频域分析与傅里叶变换

图形学中的抗锯齿问题本质上是信号处理问题。为了理解锯齿现象的产生机制，需要从频域的角度分析图像信号。

傅里叶变换（Fourier Transform）：

一维信号的傅里叶变换定义为：

\[F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t} dt\]

二维图像的傅里叶变换：

\[F(\omega_x, \omega_y) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x,y) e^{-j(\omega_x x + \omega_y y)} dx dy\]

频域特性：

低频分量：对应图像的整体结构和平滑区域
高频分量：对应图像的细节、边缘和纹理
频谱宽度：反映信号变化的快慢程度

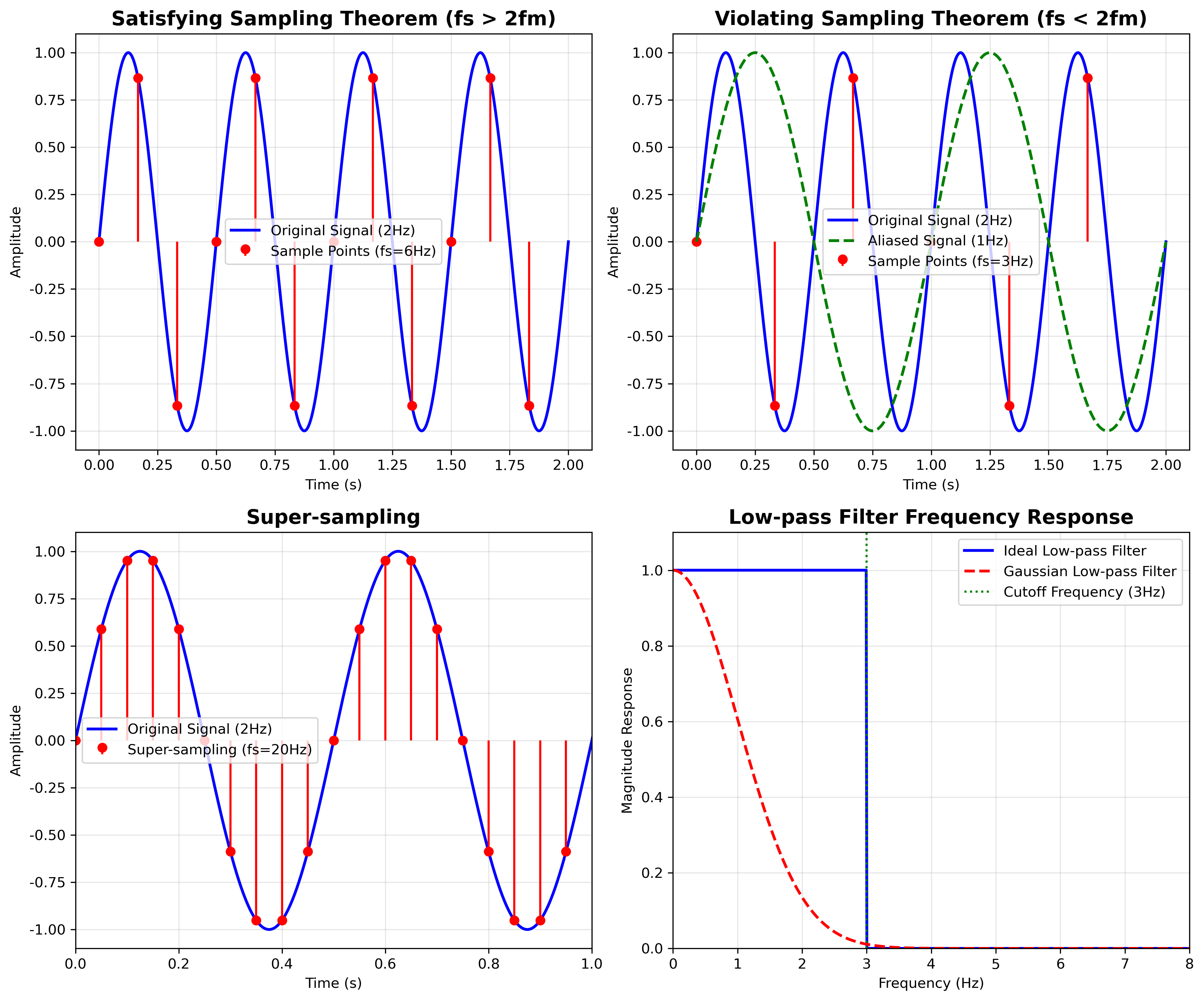
采样定理与奈奎斯特频率

奈奎斯特-香农采样定理（Nyquist-Shannon Sampling Theorem）

定理陈述：为了完美重建原始连续信号，采样频率必须至少是信号最高频率成分的两倍。

数学表达：

\[f_s \geq 2f_{max}\]

其中：

$f_s$ 是采样频率
$f_{max}$ 是信号的最高频率
$f_N = f_s/2$ 称为奈奎斯特频率

关键概念：

欠采样（Under-sampling）：当 $f_s < 2f_{max}$ 时发生
混叠（Aliasing）：高频信号被误认为低频信号
锯齿现象：混叠在图形学中的表现形式

混叠的数学原理

当信号被采样时，频谱会在频域中周期性重复：

\[F_s(\omega) = \frac{1}{T} \sum_{n=-\infty}^{\infty} F(\omega - n\omega_s)\]

如果原信号带宽超过奈奎斯特频率，重复的频谱会重叠，产生混叠。

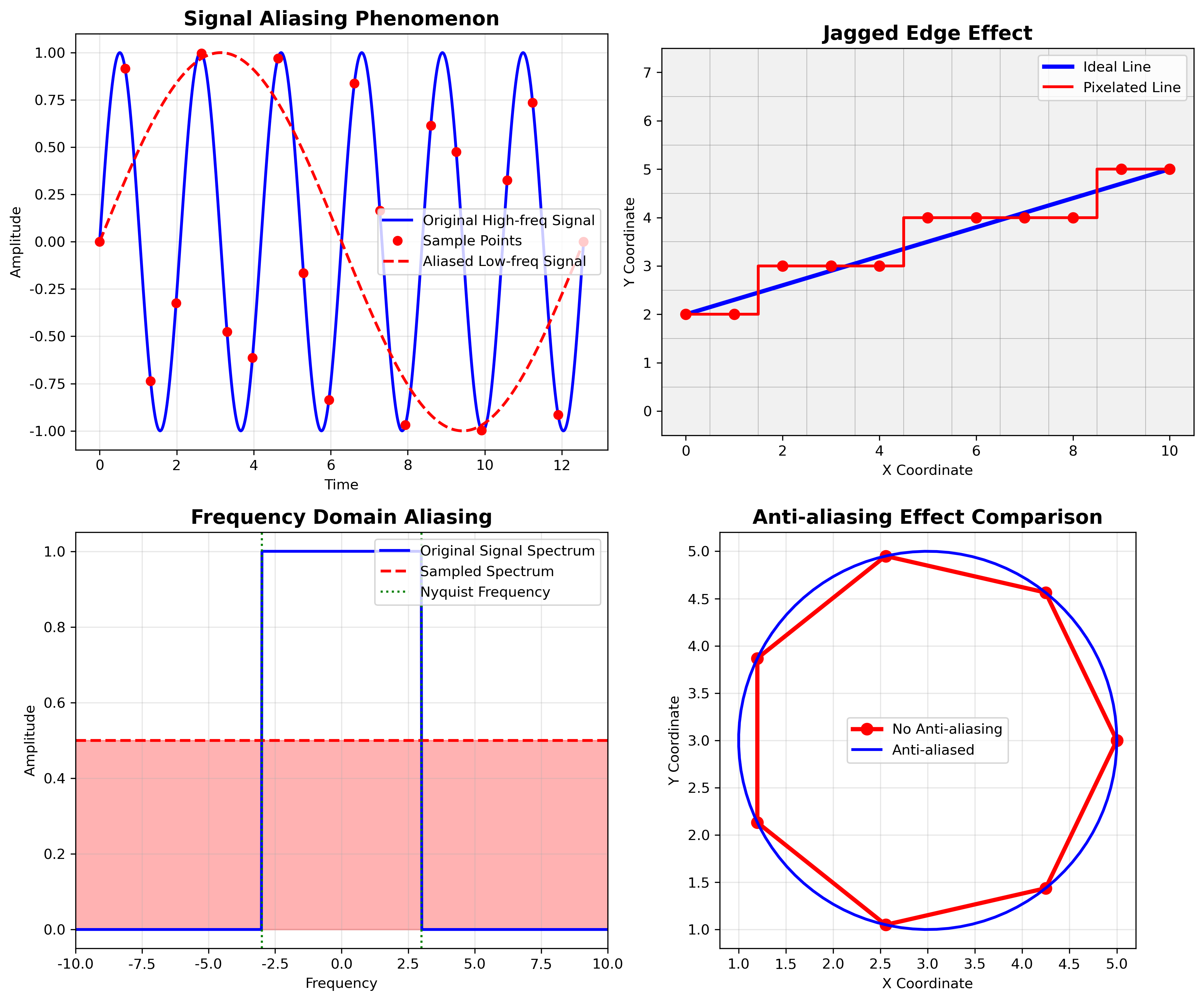
采样定理演示：左上图满足采样定理的情况，右上图违反采样定理导致混叠，左下图展示超采样效果，右下图显示低通滤波器的频率响应

锯齿现象的产生机制

锯齿产生的根本原因

1. 几何混叠：

连续的几何对象（直线、曲线、边界）包含无限高的频率成分
有限分辨率的显示设备无法表示这些高频细节
高频信息被错误地表示为低频锯齿

2. 时域混叠：

动画中快速运动的对象
帧率不足导致的运动模糊和跳跃

3. 纹理混叠：

高分辨率纹理映射到远距离小像素区域
纹理的高频细节产生闪烁和摩尔纹

锯齿的视觉表现

阶梯状边缘：直线和曲线边界呈现锯齿形
摩尔纹（Moiré Pattern）：规则纹理产生的干涉条纹
闪烁（Flickering）：动画中的时间性锯齿
爆裂感（Popping）：纹理细节的突然出现和消失

抗锯齿技术演示：左上图展示信号混叠现象，右上图显示锯齿边缘效果，左下图说明频域混叠原理，右下图对比抗锯齿前后效果

抗锯齿技术分类

预滤波（Pre-filtering）技术

低通滤波

通过移除信号中的高频成分来防止混叠：

理想低通滤波器：

\[H(\omega) = \begin{cases} 1, & \lvert\omega\rvert \leq \omega_c \\ 0, & \lvert\omega\rvert > \omega_c \end{cases}\]

其中 $\omega_c$ 是截止频率，通常设为 $\omega_c = \omega_s/2$。

实际应用中的低通滤波：

高斯滤波器：$H(\omega) = e^{-\omega^2/(2\sigma^2)}$
Lanczos滤波器：具有较好的频率响应特性
Mitchell滤波器：在保持锐度和减少振铃间平衡

解析预滤波

对于简单几何图形，可以解析计算覆盖面积：

直线的解析抗锯齿：

计算直线在每个像素中的精确覆盖面积
根据覆盖面积设置像素强度
Wu’s反锯齿直线算法是经典实现

后处理（Post-processing）技术

超采样（Super-sampling）

基本思想：在更高分辨率下渲染，然后降采样到目标分辨率。

实现步骤：

上采样渲染：以 $n \times n$ 倍分辨率渲染场景
滤波降采样：使用适当的滤波器合并子像素
重建图像：生成最终的抗锯齿图像

常用采样模式：

均匀网格采样：规则 $n \times n$ 子像素网格
抖动采样（Jittered Sampling）：在网格基础上添加随机偏移
泊松盘采样：保持最小距离的随机分布

多重采样抗锯齿（MSAA）

现代GPU硬件支持的高效抗锯齿技术：

技术特点：

几何边缘进行多重采样
着色计算只在像素中心进行一次
大大降低了计算开销

采样模式：

2x MSAA：每像素2个采样点
4x MSAA：每像素4个采样点
8x MSAA：每像素8个采样点

区域采样（Area Sampling）

像素覆盖面积计算

将像素视为有限面积的区域，计算几何对象对该区域的覆盖：

\[I_{pixel} = \frac{1}{A_{pixel}} \iint_{pixel} I(x,y) \, dx dy\]

优势：

理论上精确的抗锯齿
适用于矢量图形和字体渲染

挑战：

复杂几何的面积计算困难
计算开销较大

A-buffer算法

A-buffer（Anti-aliased buffer）存储每个像素的完整几何信息：

片元列表：记录所有相交的几何片元
覆盖面积：每个片元的精确覆盖面积
最终合成：根据覆盖面积加权平均

纹理抗锯齿

MIP映射（MIP Mapping）

MIP映射是纹理抗锯齿的核心技术，通过预计算多级纹理来避免纹理混叠。

MIP映射原理

MIP级别计算：

根据纹理坐标的变化率计算合适的MIP级别：

\[\lambda = \log_2\left(\max\left(\sqrt{\left(\frac{\partial u}{\partial x}\right)^2 + \left(\frac{\partial v}{\partial x}\right)^2}, \sqrt{\left(\frac{\partial u}{\partial y}\right)^2 + \left(\frac{\partial v}{\partial y}\right)^2}\right)\right)\]

三线性插值：

在相邻两个MIP级别间进行插值：

双线性插值：在每个MIP级别内进行2D插值
级别间插值：在两个MIP级别的结果间插值
最终结果：获得平滑的纹理过渡

MIP映射的局限性

各向异性过滤不足：MIP映射假设投影是各向同性的
过度模糊：远距离纹理可能过于模糊
内存开销：需要额外33%的纹理内存

各向异性过滤

Ripmap技术

扩展MIP映射以处理各向异性情况：

多级纹理：预计算 $2^m \times 2^n$ 尺寸的所有组合
方向敏感：根据纹理坐标的梯度选择合适级别
内存开销：是MIP映射的3倍

EWA过滤（Elliptical Weighted Average）

原理：

将像素在纹理空间的投影近似为椭圆
对椭圆覆盖区域进行加权平均采样
支持任意角度和长宽比的各向异性

实现关键：

雅可比矩阵：计算屏幕空间到纹理空间的变换
椭圆参数：确定采样椭圆的大小、方向和离心率
高斯权重：使用高斯函数作为采样权重

时间抗锯齿

运动模糊

快门模型

模拟真实相机的快门效果：

\[I(x,y) = \frac{1}{\Delta t} \int_0^{\Delta t} I(x - v_x \cdot t, y - v_y \cdot t) dt\]

其中 $(v_x, v_y)$ 是像素的运动速度向量。

实现方法

1. 多帧累积：

在快门时间内渲染多个帧
对所有帧进行平均

2. 速度缓冲：

计算每个像素的运动向量
沿运动方向进行滤波

时间采样

随机时间采样

使用随机时间点进行采样，减少规律性时间混叠：

泊松采样：在时间轴上进行泊松分布采样
蓝噪声采样：具有良好频谱特性的采样模式

现代抗锯齿技术

形态学抗锯齿（MLAA）

基于图像形态学的后处理抗锯齿：

算法步骤：

边缘检测：识别图像中的锯齿边缘
模式识别：检测常见的锯齿模式
边缘重建：使用平滑曲线替代锯齿边缘

快速近似抗锯齿（FXAA）

轻量级的后处理抗锯齿技术：

特点：

单通道后处理
基于亮度梯度检测边缘
计算开销极低
适合实时应用

时间抗锯齿（TAA）

结合时间信息的抗锯齿技术：

核心思想：

利用历史帧信息
子像素级别的时间重投影
减少当前帧的采样需求