VCI - 4: 2D图形绘制

扫描转换与光栅化

扫描转换（Scan Conversion）

扫描转换，也称为光栅化（Rasterization），是将理想几何图形转换为像素表示的过程。

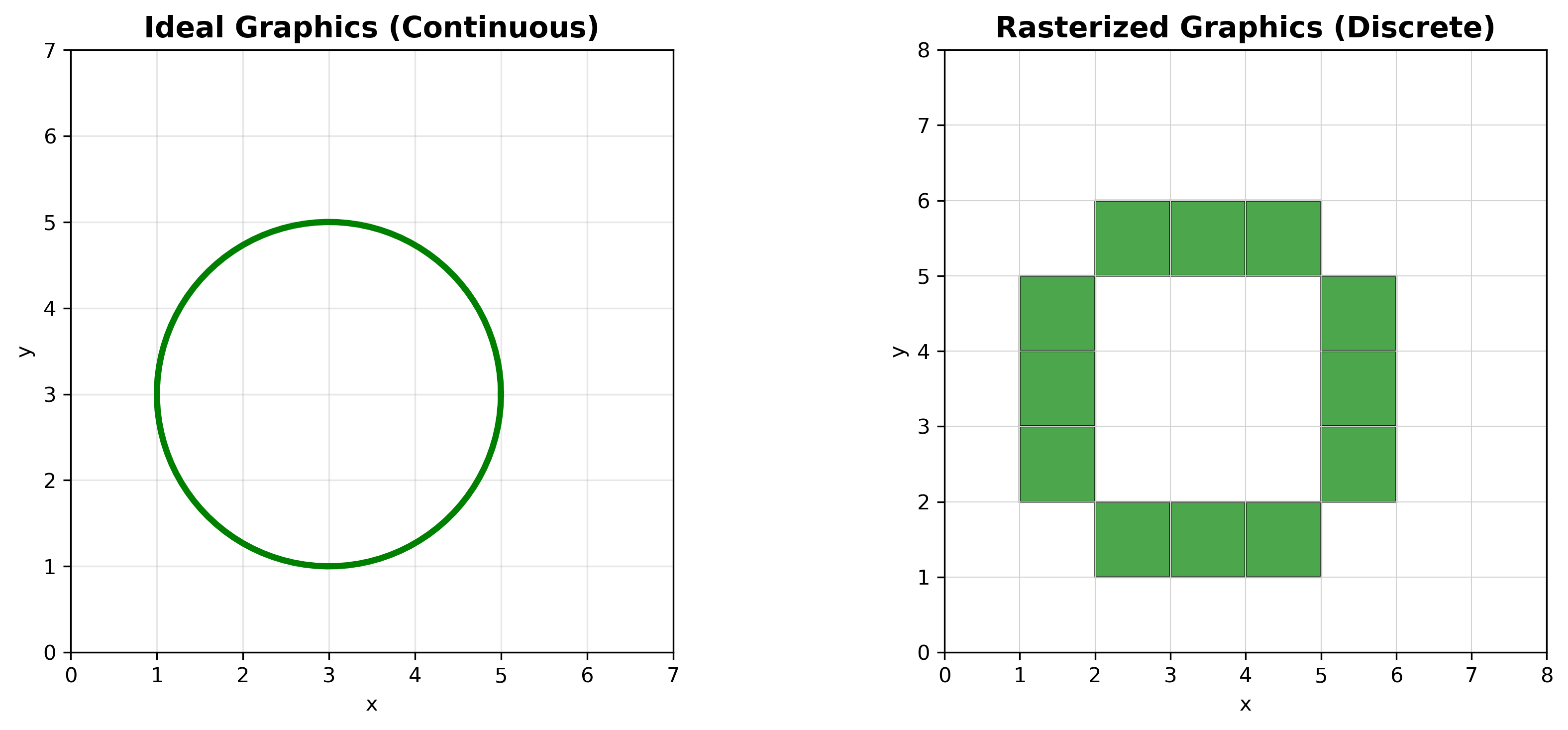
扫描转换过程：从理想的连续图形（左）到离散的像素表示（右）

基本概念：

理想图形是连续的几何对象
光栅显示设备由离散的像素组成
扫描转换将连续图形近似为离散像素

扫描转换算法的性质

良好扫描转换算法的特性：

准确性（Accuracy）：正确近似理想图形
效率（Efficiency）：快速计算

实现挑战：

修改所有正确的像素
只修改正确的像素
正确计算像素值
快速执行算法

设计原则：首先实现正确的算法，然后进行优化

直线绘制算法

简单直线算法

最基础的直线绘制方法使用直线方程 y(x) = mx + b：

void line(int x0, int y0, int x1, int y1) {
    float m = whatever;
    float b = whatever;
    int x;
    for(x=x0; x<=x1; x++) {
        float y = m*x + b;
        draw_pixel(x, Round(y));
    }
}

缺点：

需要浮点乘法和加法
需要浮点取整操作
计算效率低

DDA算法（Digital Differential Analyzer）

DDA算法通过增量计算避免乘法运算：

void line(int x0, int y0, int x1, int y1) {
    float y = y0;
    float m = (y1 - y0) / (float)(x1 - x0);
    int x;
    for(x=x0; x<=x1; x++) {
        draw_pixel(x, Round(y));
        y += m;
    }
}

优化原理：

如果已知 y(x)，可以计算 y(x+1) = y(x) + m
避免了循环内的乘法运算

问题：仍需浮点加法和取整运算

Bresenham算法

Bresenham算法是最高效的直线绘制算法，仅使用整数运算：

void draw_line(int x0, int y0, int x1, int y1) {
    int x, y = y0;
    int dx = 2*(x1-x0), dy = 2*(y1-y0);
    int dydx = dy-dx, F = dy-dx/2;

    for(x=x0; x<=x1; x++) {
        draw_pixel(x, y);
        if(F < 0)
            F += dy;
        else {
            y++;
            F += dydx;
        }
    }
}

Bresenham算法原理

核心思想

在每一步中，需要决定下一个像素的位置：

当前像素位置：(x, y)
候选下一个像素：(x+1, y) 或 (x+1, y+1)

隐式函数判断

直线的隐式函数：

直线L从 [x0, y0] 到 [x1, y1]
dx = x1 - x0, dy = y1 - y0
法向量：N = [dy, -dx]
隐式函数：F(P) = 2N·(P - P0)

判断规则：

测试中点 (x+1, y+1/2)
如果 F((x+1, y+1/2)) > 0：选择 (x+1, y+1)
如果 F((x+1, y+1/2)) ≤ 0：选择 (x+1, y)

增量更新

关键优化：增量更新决策变量F

F(P+Δ) = F(P) + 2N·Δ
Δ 为 [1,0] 或 [1,1]
只需加法运算，避免乘法

更新规则：

如果 F < 0：F = F + 2dy
如果 F ≥ 0：F = F + 2dy - 2dx

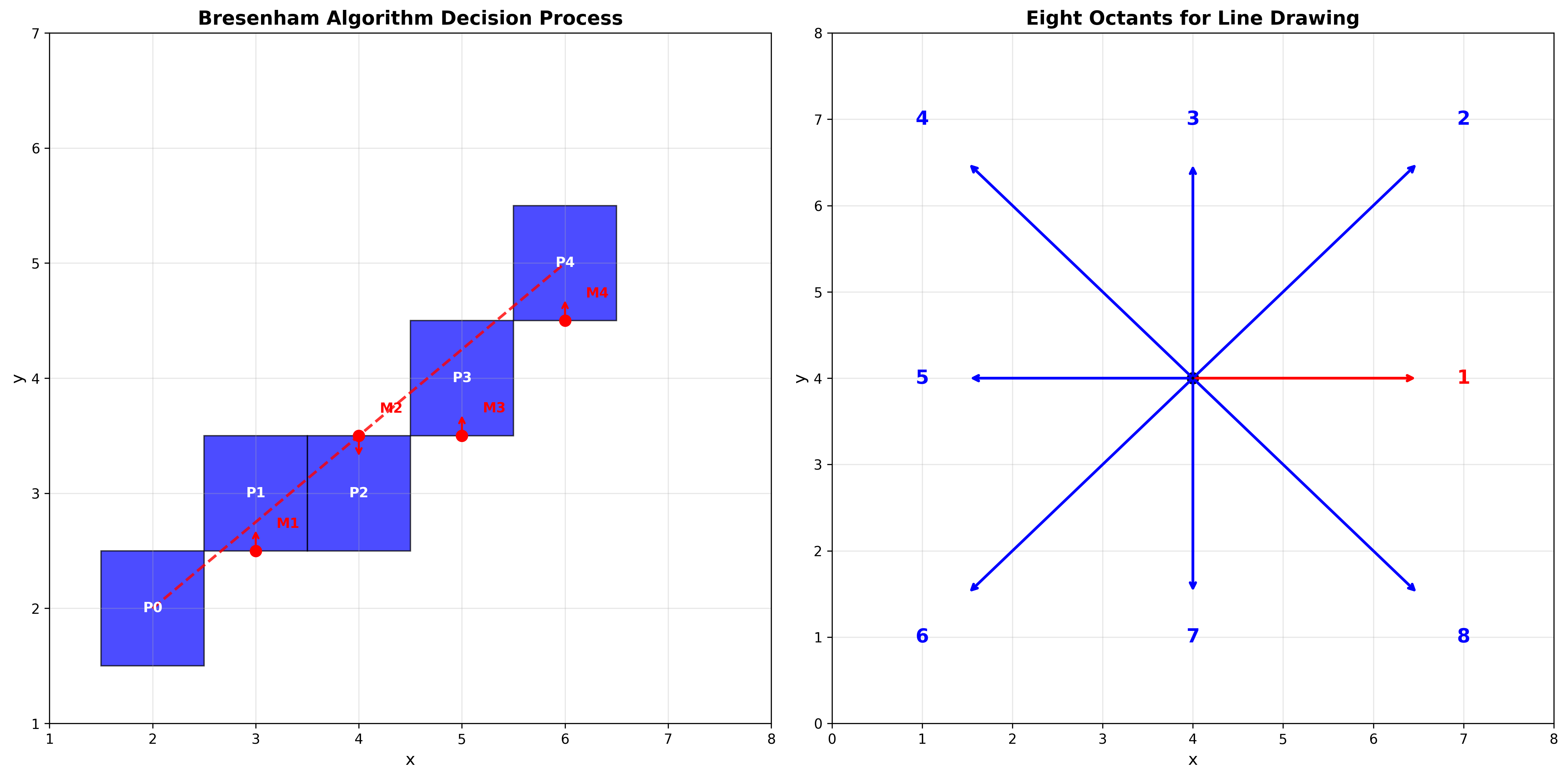
Bresenham算法示意图：左图显示算法的决策过程和中点测试，右图展示直线绘制需要处理的8个象限

不同方向的直线

直线绘制需要处理8个八分象限（octants）：

斜率的不同范围
端点顺序的不同情况

处理原则：

选择”快”方向作为主方向
每步在主方向前进一个像素
根据斜率决定是否在副方向前进

圆形绘制

Bresenham圆算法

圆形绘制采用类似直线的方法：

void draw_circle(int radius) {
    int x = 0, y = radius;
    int d = 3 - 2*radius;

    while(y > x) {
        if(d < 0) {
            d += 4*x + 6;
        } else {
            d += 4*(x-y) + 10;
            y--;
        }
        x++;
        draw_8_pts(x, y);  // 八重对称性
    }
}

特点：

使用圆的隐式函数：F = x² + y² - r²
利用八重对称性，只计算1/8圆周
通过符号变换得到完整圆形

多边形填充

凸多边形填充

算法步骤：

找到多边形的顶部和底部顶点
建立左右边界的边列表
对每条扫描线：
- 找到左右端点 xl 和 xr
- 填充 xl 到 xr 之间的像素

注意事项：

必须精确处理边界，避免相邻多边形间的缝隙或重叠
可以使用Bresenham算法计算边界点

凹多边形填充

扫描线算法：

对每条扫描线
找到所有与多边形的交点
按从左到右排序交点
使用奇偶规则（Parity Rule）填充内部区域

奇偶规则：

奇数编号的区间为内部（需要填充）
偶数编号的区间为外部（不填充）

替代方案：

将凹多边形三角剖分为多个三角形
分别填充每个三角形

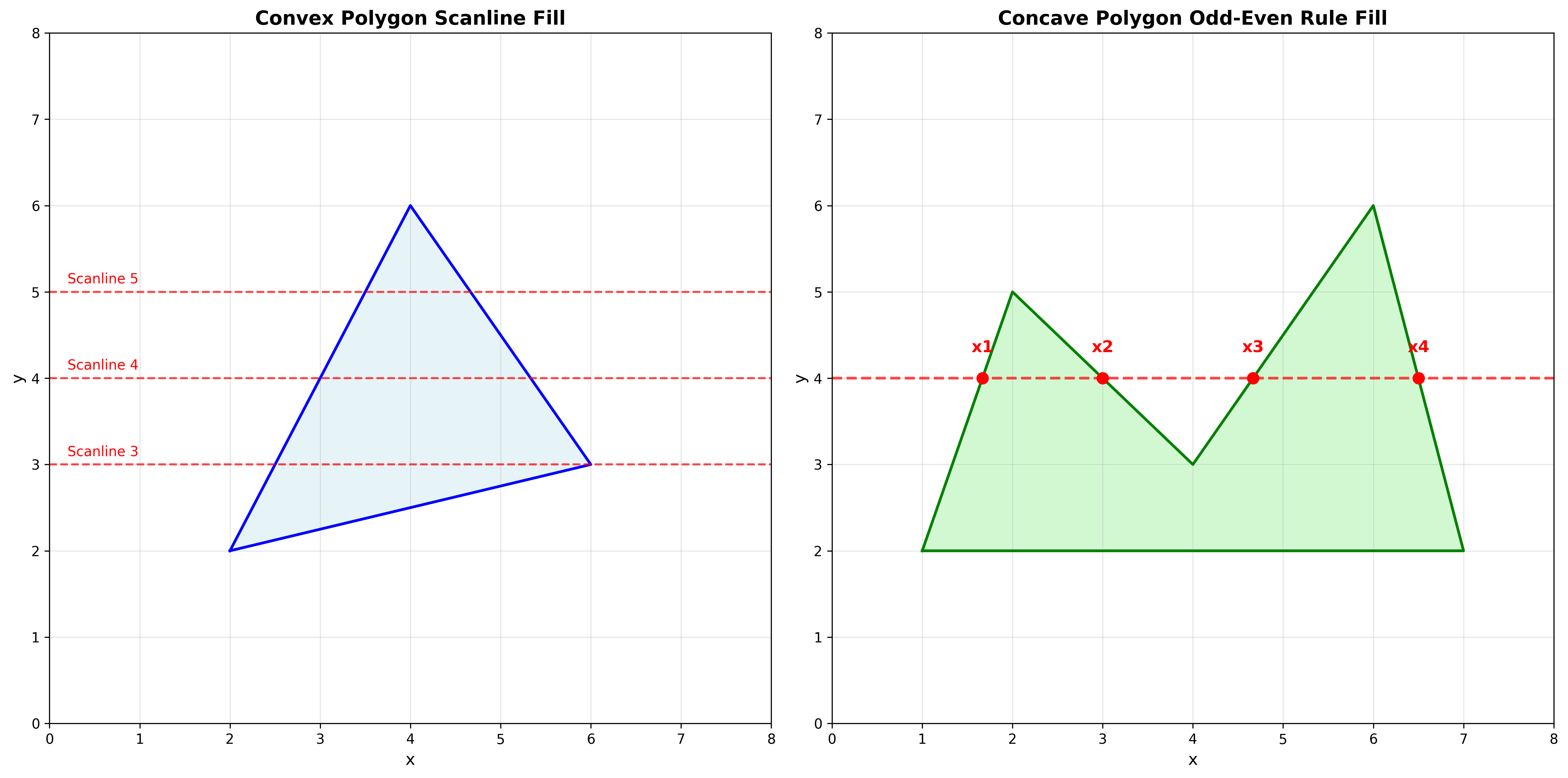
多边形填充算法：左图为凸多边形的扫描线填充，右图为凹多边形的奇偶规则填充示例

颜色插值

线性插值

在两点间进行颜色插值：

? = a(1-t) + bt = a + (b-a)t

其中 t 是插值参数（0到1之间）

双线性插值

在矩形区域内进行颜色插值：

? = a(1-dx)(1-dy) + bdx(1-dy) + c(1-dx)dy + ddxdy

步骤：

先在x方向进行两次线性插值
再在y方向进行一次线性插值

三角形内颜色插值

对于具有顶点颜色的三角形，使用重心坐标进行插值：

每个顶点有颜色值 (r0,g0,b0), (r1,g1,b1), (r2,g2,b2)
三角形内任意点的颜色通过重心坐标加权平均得到

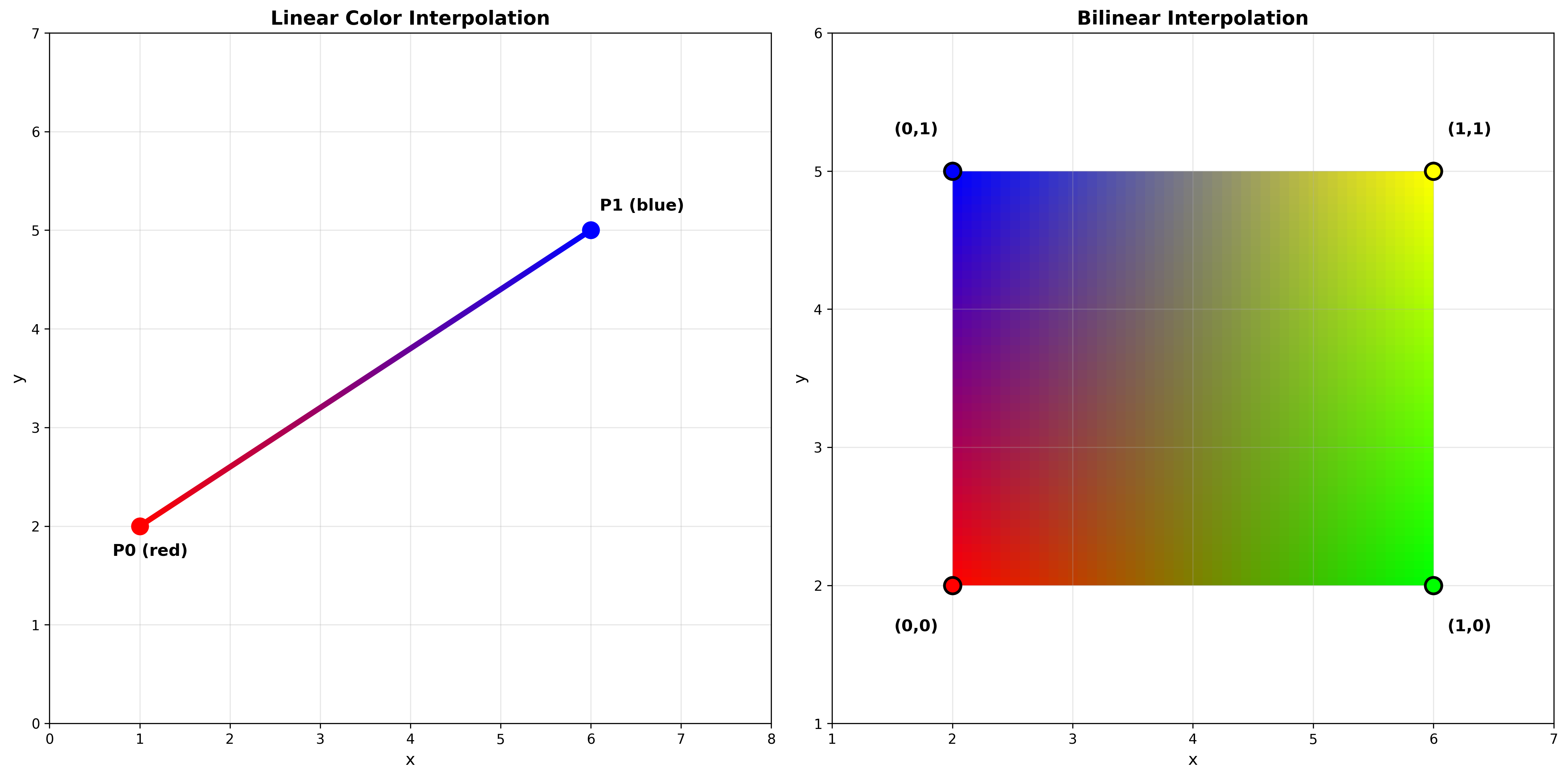
颜色插值算法：左图为线性插值的颜色渐变效果，右图为双线性插值在矩形区域内的插值结果

图像变形（Image Warping）

基本概念

图像变形是将图像从一个坐标系变换到另一个坐标系的过程。

常见应用：

图像校正
透视变换
艺术效果处理

变形实现

基本流程：

定义源图像和目标图像的对应关系
对目标图像的每个像素，计算对应的源图像坐标
通过插值获得目标像素的颜色值

透视校正：在透视变形中，需要考虑深度信息的影响：

非透视校正变形：直接插值可能产生不自然效果
透视校正变形：考虑深度信息的正确插值

本笔记基于北京大学视觉计算实验室陈宝权教授的VCI课程第四讲内容整理