数据结构与算法 - 第6章: 树(Tree)
树的概念
树的定义
树是包括\(n\)个结点的有限集合\(T\)(\(n \geq 1\)),使得:
- 有一个根结点
- 除根以外的其它结点被分成\(m\)个(\(m \geq 0\))不相交的集合\(T_1, T_2, \ldots, T_m\),而且这些集合的每一个又都是树。树\(T_1, T_2, \ldots, T_m\)称作这个根的子树
这是一个递归定义。
逻辑结构
包含\(n\)个结点的有穷集合\(K\)(\(n > 0\)),且在\(K\)上定义了一个关系\(N\),关系\(N\)满足以下条件:
-
有且仅有一个结点\(k_0 \in K\),它对于关系\(N\)来说没有前驱。结点\(k_0\)称作树的根
-
除\(k_0\)外,\(K\)中每个结点对于关系\(N\)来说都有且仅有一个前驱
-
除\(k_0\)外,任何结点\(k \in K\),存在一结点序列\(k_0, k_1, \ldots, k_s\),使得\(k_0\)就是树根,且\(k_s = k\),其中有序对\(\langle k_{i-1}, k_i \rangle \in N\)(\(1 \leq i \leq s\))。这样的结点序列称为从根到结点\(k\)的一条路径
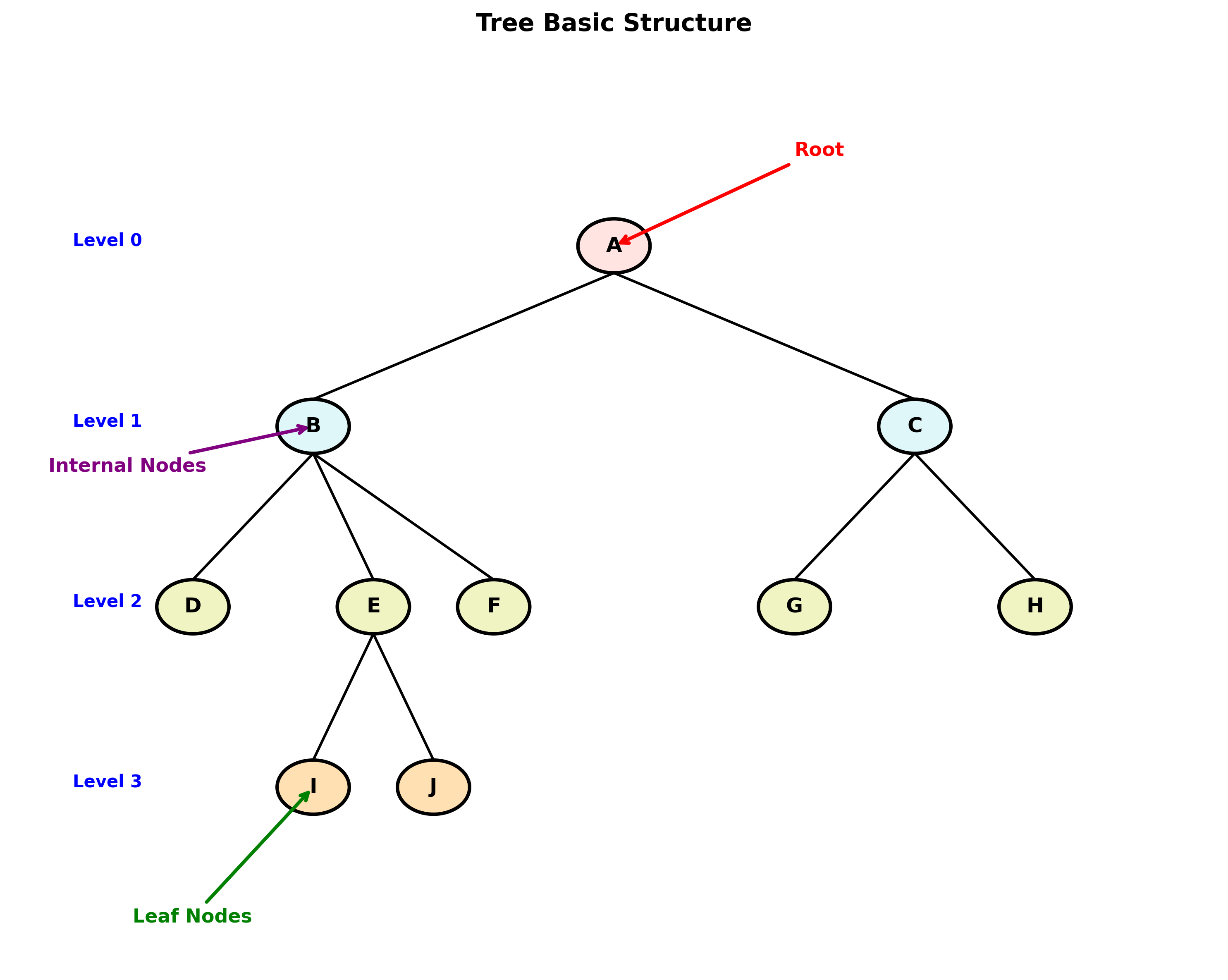
上图展示了树的基本结构,包括根结点、内部结点和叶结点。每个结点所在的层次从根结点(层次0)开始计数。
树的基本术语
- 结点(node):树中的数据元素
- 结点的度(degree):结点的子树个数
- 叶结点(leaf node):度为0的结点
- 分支结点(internal node):度不为0的结点
- 子女(children):结点的下层结点
- 双亲(parent):结点的上层结点
- 兄弟(sibling):同一双亲的子女结点
- 祖先(ancestor):从根到该结点路径上的所有结点
- 子孙(descendant):以某结点为根的子树中的所有结点
- 结点层次(level):根结点层次为0,其它结点层次等于双亲层次加1
- 树的深度/高度(depth/height):树中结点的最大层次数加1
- 树的度(degree of tree):树中所有结点度数的最大值
- 有序树(ordered tree):把树结点的子结点按从左到右的次序顺序编号
- 无序树(unordered tree):子结点无明确次序
- 森林(forest):零棵或多棵不相交的树的集合
重要区别:度为2的有序树并不是二叉树!
- 第一子结点被删除后,第二子结点自然顶替成为第1子结点
- 度为2并且严格区分左右两个子结点的有序树才是二叉树
森林
森林(forest)是零棵或多棵不相交的树的集合(通常是有序集合)。
- 对于树中的每个结点,其子树组成的集合就是森林
- 而加入一个结点作为根,森林就可以转化成一棵树了
森林与二叉树的等价转换
等价关系
树或森林与二叉树一一对应:
- 任何森林都可以用一棵二叉树唯一表达
- 任何二叉树也都唯一对应到一个森林
转换规则
树所对应的二叉树中:
- 一个结点的左子结点是它在原来树里的第一个子结点
- 右子结点是它在原来的树里的下一个兄弟
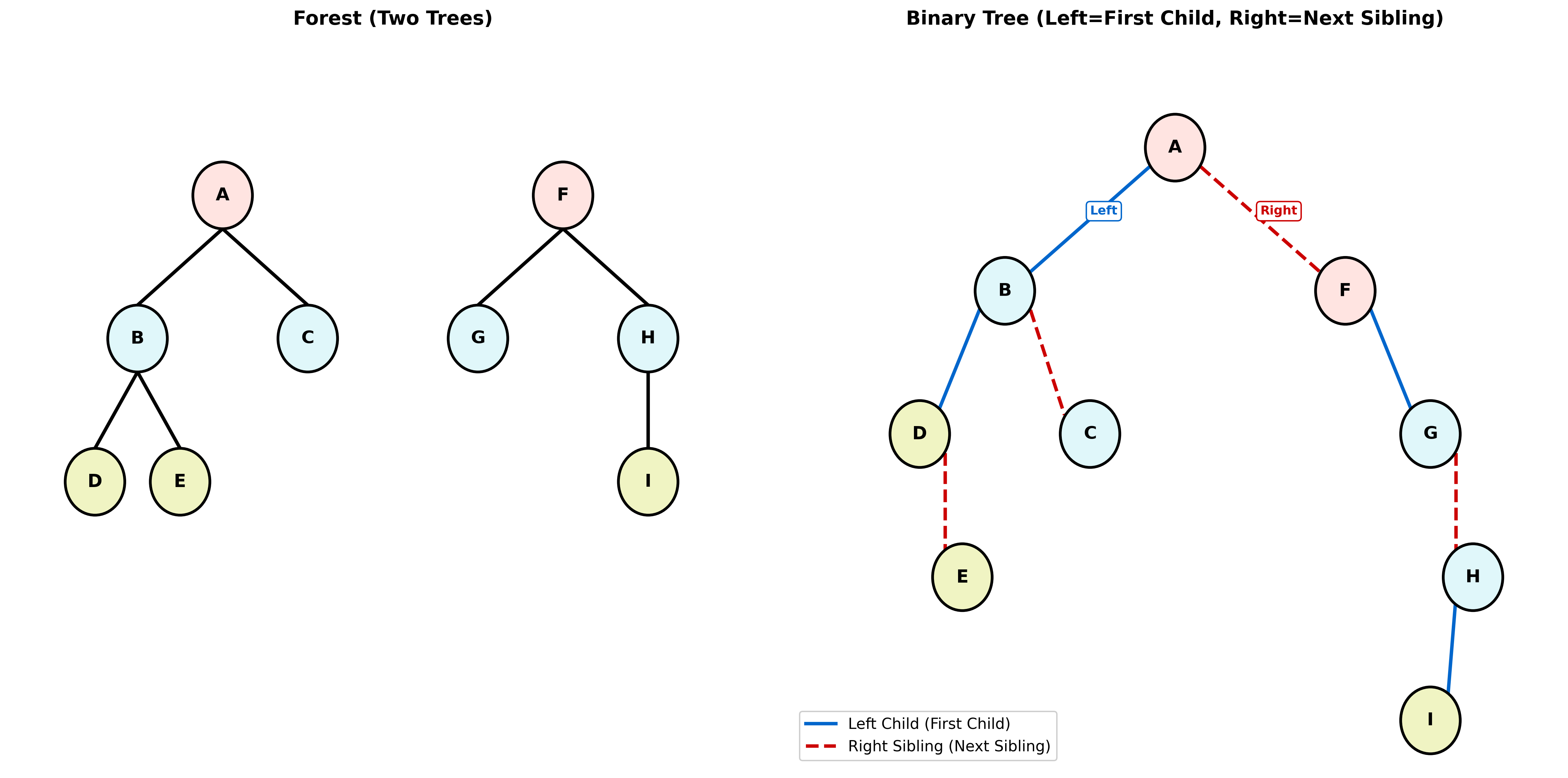
上图展示了森林到二叉树的转换过程。左侧是原始森林(两棵树),右侧是转换后的二叉树。在二叉树中,实线表示左子结点(第一个子结点),虚线表示右兄弟结点。
森林到二叉树的转换
把森林\(F\)看作树的有序集合,\(F = (T_1, T_2, \ldots, T_n)\),对应于\(F\)的二叉树\(B(F)\)的定义是:
- 若\(n = 0\),则\(B(F)\)为空
- 若\(n > 0\),则\(B(F)\)的根是\(T_1\)的根\(R_1\),\(B(F)\)的左子树是\(B(T_{11}, T_{12}, \ldots, T_{1m})\),其中\(T_{11}, T_{12}, \ldots, T_{1m}\)是\(R_1\)的子树;\(B(F)\)的右子树是\(B(T_2, \ldots, T_n)\)
转换步骤:
- 加线:在树中所有相邻的兄弟之间加一连线
- 抹线:对树中每个结点,除其最左孩子外,抹去该结点与其余孩子间的连线
- 整理:以树的根结点为轴心,将整树顺时针转45°
注意:树转换成的二叉树其右子树一定为空。
二叉树到森林的转换
设\(B\)是一棵二叉树,\(root\)是\(B\)的根,\(L\)和\(R\)分别是\(root\)的左子树和右子树,则森林\(F(B)\)的定义是:
- 若\(B\)为空,则\(F(B)\)是空的森林
- 若\(B\)不为空,则\(F(B)\)是一棵树\(T_1\)加上森林\(F(R)\),其中树\(T_1\)的根为\(root\),\(root\)的子树为\(F(L)\)
转换步骤:
- 加线:若\(p\)结点是父结点的左孩子,则将\(p\)的右孩子、右孩子的右孩子……沿分支找到的所有右孩子,都与\(p\)的双亲用线连起来
- 抹线:抹掉原二叉树中双亲与右孩子之间的连线
- 调整:将结点按层次排列,形成树结构
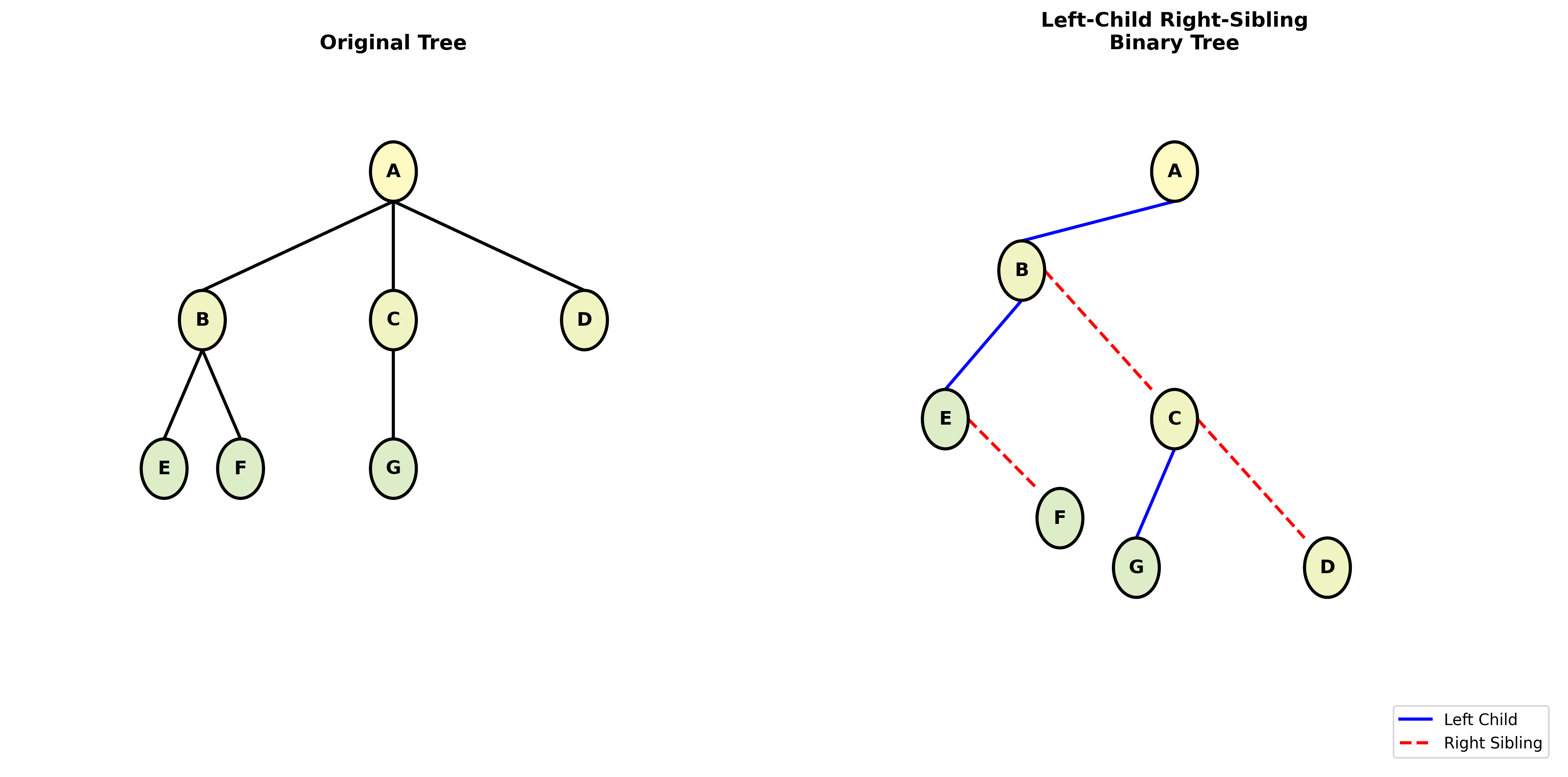
上图展示了”左子结点/右兄弟”表示法的转换关系。左侧是原始树,右侧是对应的二叉树形式。
树的抽象数据类型
树结点的ADT
template<class T>
class TreeNode {
public:
TreeNode(const T&); // 构造函数
virtual ~TreeNode(){}; // 析构函数
bool isLeaf(); // 如果结点是叶,返回true
T Value(); // 返回结点的值
TreeNode<T>* LeftMostChild(); // 返回第一个左孩子
TreeNode<T>* RightSibling(); // 返回右兄弟
void setValue(T&); // 设置结点的值
void setChild(TreeNode<T>* pointer); // 设置左子结点
void setSibling(TreeNode<T>* pointer); // 设置右兄弟
void InsertFirst(TreeNode<T>* node); // 以第一个左子结点身份插入结点
void InsertNext(TreeNode<T>* node); // 以右兄弟的身份插入结点
};
树的ADT
template <class T>
class Tree {
public:
Tree(); // 构造函数
virtual ~Tree(); // 析构函数
TreeNode<T>* getRoot(); // 返回树中的根结点
void CreateRoot(const T& rootValue); // 创建树中的根结点
bool isEmpty(); // 判断是否为空树
TreeNode<T>* Parent(TreeNode<T>* current); // 返回current结点的父结点
TreeNode<T>* PrevSibling(TreeNode<T>* current); // 返回前一个兄弟结点
void DeleteSubTree(TreeNode<T>* subroot); // 删除以subroot为根的子树
void RootFirstTraverse(TreeNode<T>* root); // 先根深度优先周游树
void RootLastTraverse(TreeNode<T>* root); // 后根深度优先周游树
void WidthTraverse(TreeNode<T>* root); // 宽度优先周游树
};
树(森林)的周游
深度优先周游
先根次序(Preorder)
若树非空,则遍历方法为:
- 访问根结点
- 从左到右,依次先根遍历根结点的每一棵子树
后根次序(Postorder)
若树非空,则遍历方法为:
- 从左到右,依次后根遍历根结点的每一棵子树
- 访问根结点
注意:树没有中根次序周游。
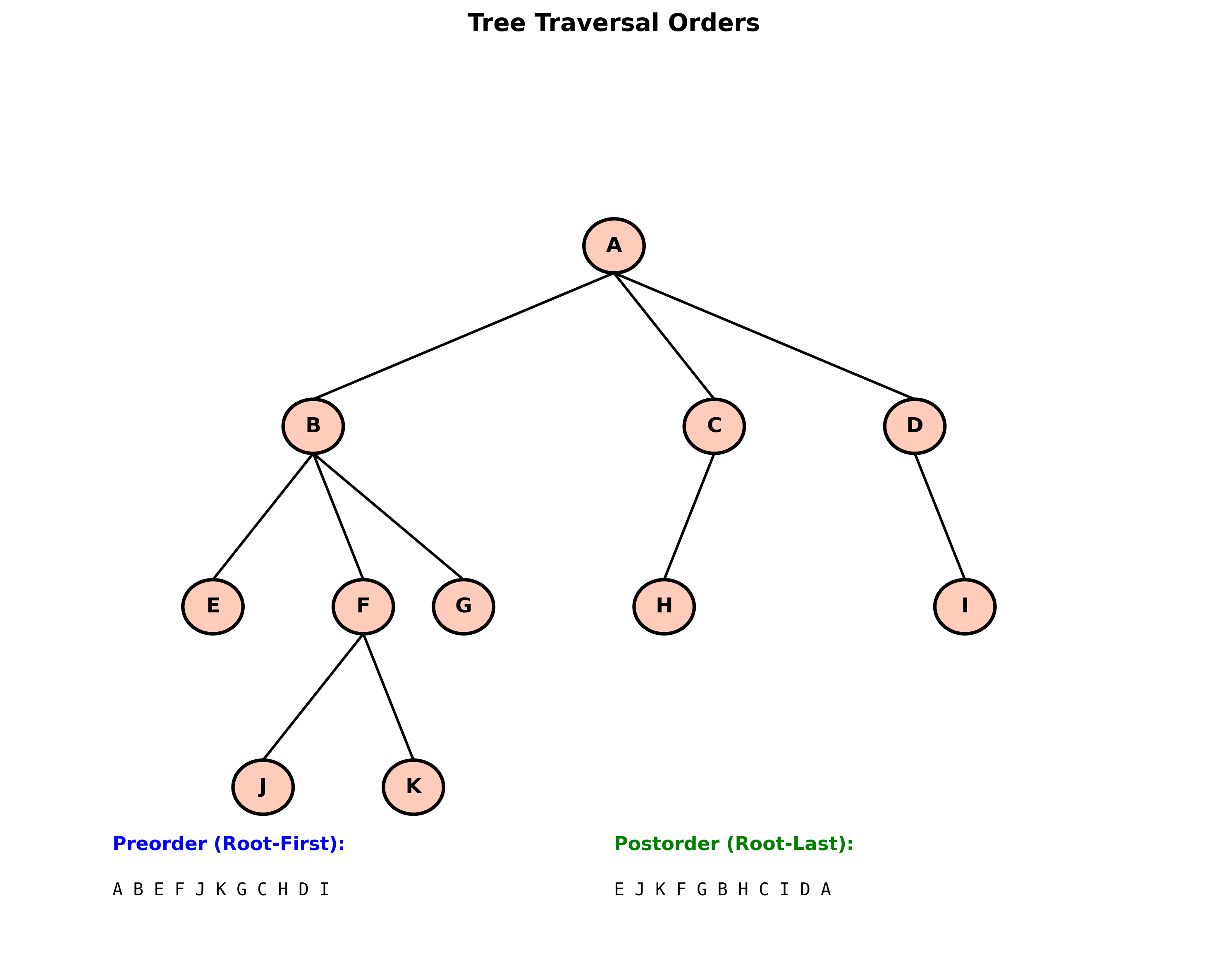
上图展示了树的先根遍历和后根遍历结果。先根遍历首先访问根结点,然后递归遍历子树;后根遍历先递归遍历子树,最后访问根结点。
周游性质
- 按先根次序周游树正好等于对应二叉树的前序周游
- 按后根次序周游树正好等于对应二叉树的中序周游
先根深度优先周游算法
template <class T>
void Tree<T>::RootFirstTraverse(TreeNode<T>* root) {
while (root != NULL) {
Visit(root->Value()); // 访问当前结点
RootFirstTraverse(root->LeftMostChild()); // 周游头一棵树根的子树
root = root->RightSibling(); // 周游其他的树
}
}
后根深度优先周游算法
template <class T>
void Tree<T>::RootLastTraverse(TreeNode<T>* root) {
while (root != NULL) {
RootLastTraverse(root->LeftMostChild()); // 周游头一棵树根的子树
Visit(root->Value()); // 访问当前结点
root = root->RightSibling(); // 周游其他的树
}
}
广度优先周游
思想:先访问层数为0的结点;然后从左到右逐个访问层数为1的结点;……;依此类推,直到访问完树中的全部结点。
实现:使用队列数据结构
template<class T>
void Tree<T>::WidthTraverse(TreeNode<T>* root) {
using std::queue;
queue<TreeNode<T>*> aQueue;
TreeNode<T>* pointer = root;
// 森林中所有根结点进入队列
while (pointer != NULL) {
aQueue.push(pointer);
pointer = pointer->RightSibling();
}
while (!aQueue.empty()) {
pointer = aQueue.front(); // 获得队首元素
aQueue.pop(); // 当前结点出队列
Visit(pointer->Value()); // 访问当前结点
pointer = pointer->LeftMostChild(); // 指向最左孩子
// 当前结点的子结点进队列
while (pointer != NULL) {
aQueue.push(pointer);
pointer = pointer->RightSibling();
}
}
}
树的链式存储
树的链式存储有多种表示法:
- 子结点表表示法
- 动态结点表示法
- 静态”左子结点/右兄弟结点”表示法
- 动态”左子结点/右兄弟结点”表示法
- 父指针表示法
子结点表表示法
每个结点包含:
- 值域
- 父结点指针
- 子结点链表
优点:
- 查找孩子个数和结点的值容易
- 树的归并容易(只需一棵树的根添到另一棵树的孩子结点表中即可)
缺点:
- 找兄弟结点困难
动态结点表示法
指针数组法
每个结点包含:
- 值域
- 度数域
- 指向子结点的指针数组
指针链表法
每个结点包含:
- 值域
- 指向第一个子结点的指针
- 指向子结点链表的指针
静态”左子结点/右兄弟结点”表示法
使用数组存储结点,每个结点包含:
- 值域
- 父结点索引
- 左子结点索引
- 右兄弟结点索引
优点:
- 比子结点表表示法空间效率更高
- 结点数组中的每个结点仅需要固定大小的存储空间
- 树的合并简单(如果两棵树在同一个数组中)
动态”左子结点/右兄弟结点”二叉链表表示法
本质:使用二叉树来替换树
基本思想:
- 左孩子在树中是结点的最左子结点
- 右子结点是结点原来的右侧兄弟结点
- 根的右链就是森林中每棵树的根结点
私有成员变量:
private:
T m_Value; // 树结点的值
TreeNode<T>* pChild; // 左孩子
TreeNode<T>* pSibling; // 右兄弟
成员函数实现示例:
template<class T>
bool TreeNode<T>::isLeaf() {
if (pChild == NULL)
return true;
return false;
}
template<class T>
void TreeNode<T>::InsertFirst(TreeNode<T>* node) {
if (pChild) {
node->pSibling = pChild;
pChild = node;
} else {
pChild = node;
}
}
父指针表示法
在某些应用中,只需要知道父结点情况,因此每个结点只需要保存一个指向其父结点的指针域。
特点:
- 用数组存储树所有结点
- 在每个结点中附设一个”指针”指示其父结点的位置
- 由于树中每一个结点的父指针是唯一的,所以父指针表示法可以唯一表示一棵树
基本操作:
- 查询结点的根:从一个结点出发找出一条向上延伸到达根的祖先路径 — \(O(k)\),\(k\)为树高
- 判断两个结点是否在同一棵树:两个结点根结点相同,它们一定在同一棵树中
优点:
- 寻找父结点只需\(O(k)\)时间
- 求树根结点非常方便
缺点:
- 寻兄弟节点麻烦,需要查询整个树结构
- 没有标识节点的左右次序,适合无序树的情况
并查集(Union-Find)
基本概念
并查集是一种特殊集合,由不相交子集构成。
基本操作:
- Find:判断两个结点是否在同一个集合中
- Union:归并两个集合
并查集可用于求解等价类问题。
等价关系
一个具有\(n\)个元素的集合\(S\),另有一个定义在集合\(S\)上的\(r\)个关系的关系集合\(R\)。\(x, y, z\)表示集合中的元素。
若关系\(R\)是一个等价关系,当且仅当如下条件为真时成立:
- 对于所有的\(x\),有\((x, x) \in R\)(即关系是自反的)
- 当且仅当\((x, y) \in R\)时\((y, x) \in R\)(即关系是对称的)
- 若\((x, y) \in R\)且\((y, z) \in R\),则有\((x, z) \in R\)(即关系是传递的)
如果\((x, y) \in R\),则元素\(x\)和\(y\)是等价的。
并查算法
初始状态:每个元素都在独立的只包含一个结点的树中,而它自己就是根结点。
算法流程:
- 使用
Different函数,判断一个等价对中的两个元素是否在同一棵树中- 如果是,由于它们已经在同一个等价类中,不需要作变动
- 否则两个等价类可以用
Union函数归并
树结点的ADT
template<class T>
class ParTreeNode {
private:
T value; // 结点的值
ParTreeNode<T>* parent; // 父结点指针
int nCount; // 以此结点为根的子树的总结点个数
public:
ParTreeNode(); // 构造函数
virtual ~ParTreeNode(){}; // 析构函数
T getValue(); // 返回结点的值
void setValue(const T& val); // 设置结点的值
ParTreeNode<T>* getParent(); // 返回父结点指针
void setParent(ParTreeNode<T>* par); // 设置父结点指针
int getCount(); // 返回结点数目
void setCount(const int count); // 设置结点数目
}
树的ADT
template<class T>
class ParTree {
public:
ParTreeNode<T>* array; // 存储树结点的数组
int Size; // 数组大小
ParTree(const int size); // 构造函数
virtual ~ParTree(); // 析构函数
// 查找node结点所属子树的根结点
ParTreeNode<T>* Find(ParTreeNode<T>* node) const;
// 把下标为i,j的结点所属子树合并
void Union(int i, int j);
// 判定下标为i,j的结点是否在一棵树中
bool Different(int i, int j);
};
Find操作
template <class T>
ParTreeNode<T>* ParTree<T>::Find(ParTreeNode<T>* node) const {
ParTreeNode<T>* pointer = node;
while (pointer->getParent() != NULL)
pointer = pointer->getParent();
return pointer;
}
Different操作
template<class T>
bool ParTree<T>::Different(int i, int j) {
ParTreeNode<T>* pointeri = Find(&array[i]); // 找到结点i的根
ParTreeNode<T>* pointerj = Find(&array[j]); // 找到结点j的根
return pointeri != pointerj;
}
Union操作(重量权衡合并规则)
template<class T>
void ParTree<T>::Union(int i, int j) {
ParTreeNode<T>* pointeri = Find(&array[i]);
ParTreeNode<T>* pointerj = Find(&array[j]);
if (pointeri != pointerj) {
if (pointeri->getCount() >= pointerj->getCount()) {
pointerj->setParent(pointeri);
pointeri->setCount(pointeri->getCount() + pointerj->getCount());
} else {
pointeri->setParent(pointerj);
pointerj->setCount(pointeri->getCount() + pointerj->getCount());
}
}
}
重量权衡合并规则(Weighted Union Rule)
将结点较少树的根结点指向结点较多树的根结点,这可以把树的整体深度限制在\(O(\log n)\)。
原理:
- 当处理完\(n\)个元素后,任何结点的深度最多只会增加\(\log n\)次
- 每次归并,最大高度最多增加1
- 而结点个数成倍增加
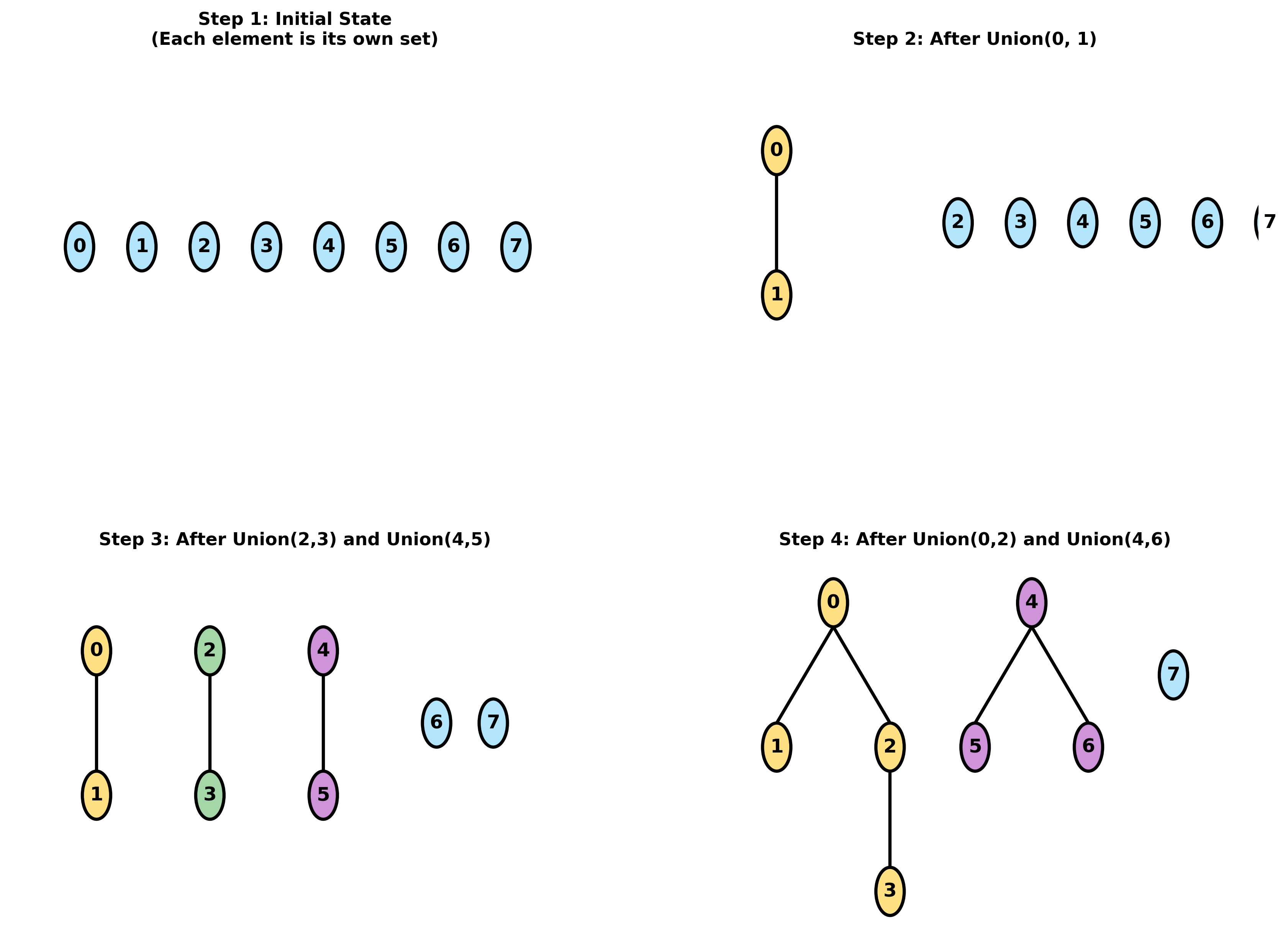
上图展示了并查集的基本操作流程。从初始状态(每个元素独立)开始,通过一系列Union操作,逐步将元素合并到不同的集合中。使用重量权衡规则可以保持树的平衡性。
路径压缩算法
template <class T>
ParTreeNode<T>* ParTree<T>::FindPC(ParTreeNode<T>* node) const {
if (node->getParent() == NULL)
return node;
node->setParent(FindPC(node->getParent()));
return node->getParent();
}
思想:
- 查找\(X\)时,设\(X\)最终到达根\(R\)
- 顺着由\(X\)到\(R\)的路径把每个结点的父指针域均设置为直接指向\(R\)
- 产生极浅树
复杂度分析
假设同时使用了”重量权衡合并规则”和”路径压缩”:
| 操作 | 平均情况 | 最坏情况 |
|---|---|---|
| Space | \(O(n)\) | \(O(n)\) |
| Find | \(O(\alpha(n))\) | \(O(\alpha(n))\) |
| Union | \(O(\alpha(n))\) | \(O(\alpha(n))\) |
其中\(O(\alpha(n))\)是一个增长非常缓慢的Ackermann函数,可以认为\(\alpha(n)\)是一个小于5的常数。
树的顺序存储
按照树遍历的次序进行节点存储:
- 带右链的先根次序表示法
- 带双标记位的先根次序表示法
- 带度数的后根次序表示法
- 带双标记的层次次序表示
关键:如何还原出树的结构
带右链的先根次序表示法
先根遍历特点:
- 任何结点的子树的所有结点都直接跟在该结点之后
- 每棵子树的所有结点都聚集在一起,中间不会插入别的结点
- 任何一个分支结点后面跟的都是它的第一个子结点(如果存在的话)
结点结构:
-
info:结点数据 -
ltag:左标记(1位)- 0:有子结点
- 1:没有子结点
-
rlink:右指针,指向下一个兄弟
特点:
- 与二叉链表相比,用
ltag代替llink,占用存储单元少,但并不丢失信息 - 可以从结点的次序和
ltag的值完全推知llink
带双标记位的先根次序表示法
事实上,带右链的先根次序表示法中rlink也不是必需的,以1位的rtag就足以表示出整个森林的结构信息。
结点结构:
-
info:结点数据 -
ltag:左标记- 0:有子结点
- 1:无子结点
-
rtag:右标记- 0:有兄弟
- 1:无兄弟
重要性质:有兄弟节点与无孩子节点一一对应,满足栈特性!
规则:”有兄弟就入栈,无孩子就出栈”
- 扫描到一个
rtag为0的结点就将它进栈 - 扫描到一个
ltag为1的结点就从栈顶弹出一个结点,并为其设置rlink,下一个要读出的节点即为其兄弟节点
构造左子结点右兄弟树算法
template <class T>
Tree<T>::Tree(DualTagTreeNode<T>* nodeArray, int count) {
using std::stack;
stack<TreeNode<T>*> aStack;
TreeNode<T>* pointer = new TreeNode<T>;
root = pointer;
for (int i = 0; i < count - 1; i++) {
pointer->setValue(nodeArray[i].info);
if (nodeArray[i].rtag == 0) // 有兄弟,则压栈
aStack.push(pointer);
else
pointer->setSibling(NULL); // 无兄弟,兄弟域设为空
TreeNode<T>* temppointer = new TreeNode<T>;
if (nodeArray[i].ltag == 0) // 有孩子,则设为孩子
pointer->setChild(temppointer);
else { // 无孩子则出栈
pointer->setChild(NULL);
pointer = aStack.pop();
pointer->setSibling(temppointer);
}
pointer = temppointer;
}
pointer->setValue(nodeArray[count - 1].info);
pointer->setChild(NULL);
pointer->setSibling(NULL);
}
带度数的后根次序表示法
结点按后根次序顺序存储,结点形式为:[info, degree]
-
info:结点的数据 -
degree:结点的度数
转换思路:
- 度数为零的结点是叶子结点(也可看作一棵子树)
- 当遇到度数非零(设为\(k\))的结点时,则排在该结点之前且离它最近的\(k\)个子树的根就是该结点的\(k\)个子结点
实现:利用栈
- 遇到零度顶点就入栈
- 遇到非零\(k\)度顶点就从栈中弹出\(k\)个节点作为其子节点,然后将该非零顶点入栈
- 持续扫描,直至序列扫描完毕
带双标记的层次次序表示
结点结构:
-
info:结点数据 -
ltag:左标记- 0:有左孩子
- 1:无左孩子
-
rtag:右标记- 0:有下一个兄弟(下一个节点即为其兄弟节点)
- 1:无兄弟节点
重要性质:有孩子节点与无兄弟节点一一对应,满足队列特性!
规则:”有孩子就入队列,无右兄弟就出队列”
- 如果结点的
ltag值为1,则置其llink为空;当结点的ltag为0时,该结点入队列 - 如果结点的
rtag值为0,那么其后的结点\(y\)就是其右兄弟 - 否则,如果结点的
rtag值为1,则rlink为空,此时出队列\(x\),并将\(x\)的llink指向序列中后续结点\(y\)即可
K叉树
定义
K叉树(K-ary Tree)的结点有\(K\)个有序子结点。
特点:
- 不同于树,K叉树的结点有\(K\)个子结点,子结点数目是固定的
- 相对来说容易实现
特殊K叉树
- 满K叉树:与满二叉树类似
- 完全K叉树:与完全二叉树类似
性质:
- 二叉树的许多性质可以推广到K叉树
- 也可以把完全K叉树存储在一个数组中
本章小结
主要内容
-
树的概念
- 树的递归定义
- 基本术语
- 森林的概念
-
森林与二叉树的转换
- 一一对应关系
- 转换算法(加线、抹线、整理)
-
树的周游
- 深度优先(先根、后根)
- 广度优先(层次遍历)
- 与二叉树遍历的对应关系
-
树的存储结构
- 链式存储(多种表示法)
- 顺序存储(多种表示法)
-
并查集
- 等价关系
- Union和Find操作
- 重量权衡合并规则
- 路径压缩优化
-
K叉树
- 定义和性质
- 满K叉树和完全K叉树
重要结论
- 树的左子结点/右兄弟表示法本质上就是二叉树
- 森林与二叉树可以相互转换
- 树的先根遍历对应二叉树的前序遍历
- 树的后根遍历对应二叉树的中序遍历
- 并查集使用重量权衡+路径压缩可达到近似常数时间复杂度
思考题
-
叶结点数公式:若某树有\(n_1\)个度数为1的结点,有\(n_2\)个度数为2的结点,……有\(n_m\)个度数为\(m\)的结点,试问它有多少个叶结点?
设叶子结点数为\(n_0\),树的结点数为\(N\):
\[N = n_0 + n_1 + n_2 + \cdots + n_m\]又等于所有节点的分支数(或度数)\(+1\):
\[N = n_1 + 2n_2 + 3n_3 + \cdots + mn_m + 1\]因此:
\[n_0 = n_2 + 2n_3 + 3n_4 + \cdots + (m-1)n_m + 1\] -
任何一棵二叉树的叶结点在先序、中序和后序的遍历序列中的相对次序不发生改变
-
某二叉树的先根序列和后根序列正好相反,则该二叉树一定是:
- 树的高度等于其结点数减1
- 任一结点都只有左子结点或只有右子结点
本笔记基于北京大学《数据结构与算法》第六章内容整理
Enjoy Reading This Article?
Here are some more articles you might like to read next: