数据结构与算法 - 第5章: 二叉树(Binary Tree)
二叉树的概念
定义
二叉树(binary tree)由结点的有限集合构成:
- 或者为空集(NIL)
- 或者由一个根结点及两棵不相交的分别称作左子树和右子树的二叉树组成
这是一个递归定义。二叉树或为空集,或者空左子树,或者空右子树,或者左右子树皆空。
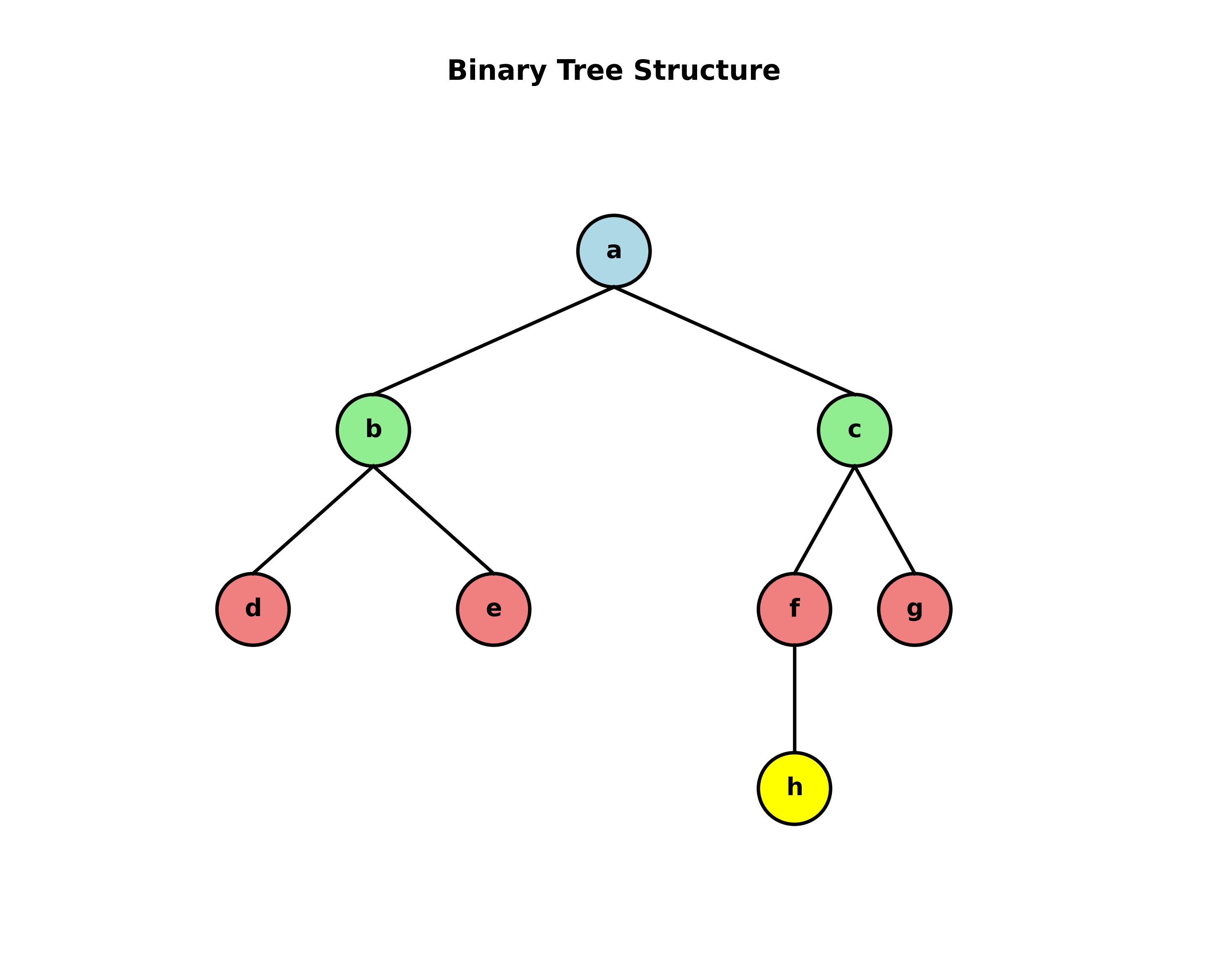
五种基本形态
二叉树具有五种基本形态:
- 空二叉树
- 根和空的左、右子树
- 根和非空左子树、空右子树
- 根和空左子树、非空右子树
- 根和非空的左、右子树
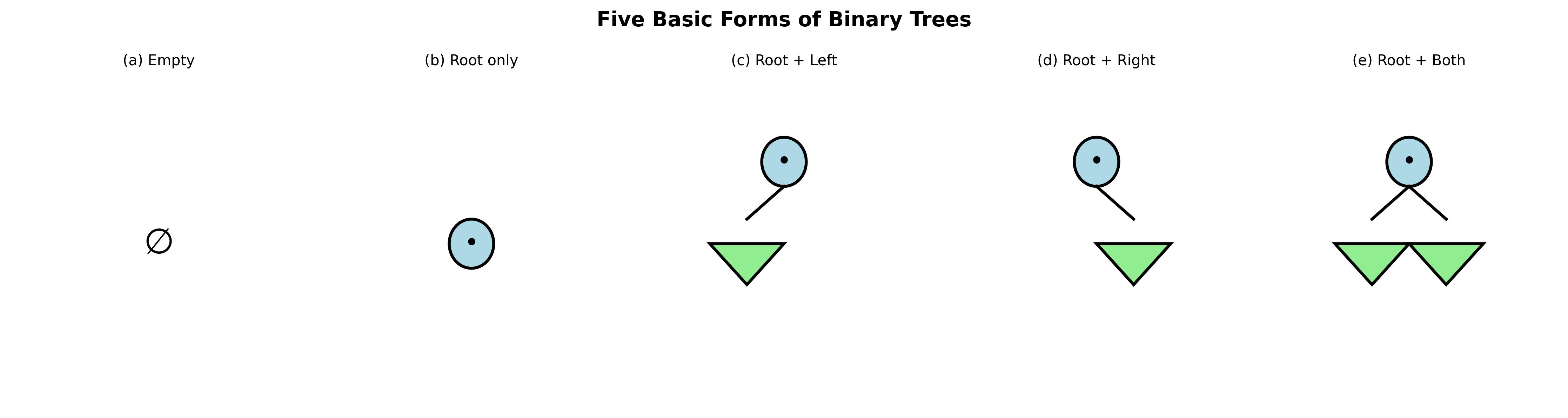
相关概念
- 父母(parent):结点的上层结点
- 子女(孩子)(children):结点的下层结点
- 边(edge):连接结点的线
- 兄弟(sibling):同一父母的子女结点
- 路径(path):从一个结点到另一结点的路线
- 祖先(ancestor):从根到该结点路径上的所有结点
- 子孙(descendant):以某结点为根的子树中的所有结点
- 树叶(leaf):度为0的结点
- 内部节点或分支节点(internal node):度不为0的结点
- 度数(degree):结点子树的数目
- 层数(level):根结点层数为0,其它结点层数等于父母层数加1
特殊二叉树
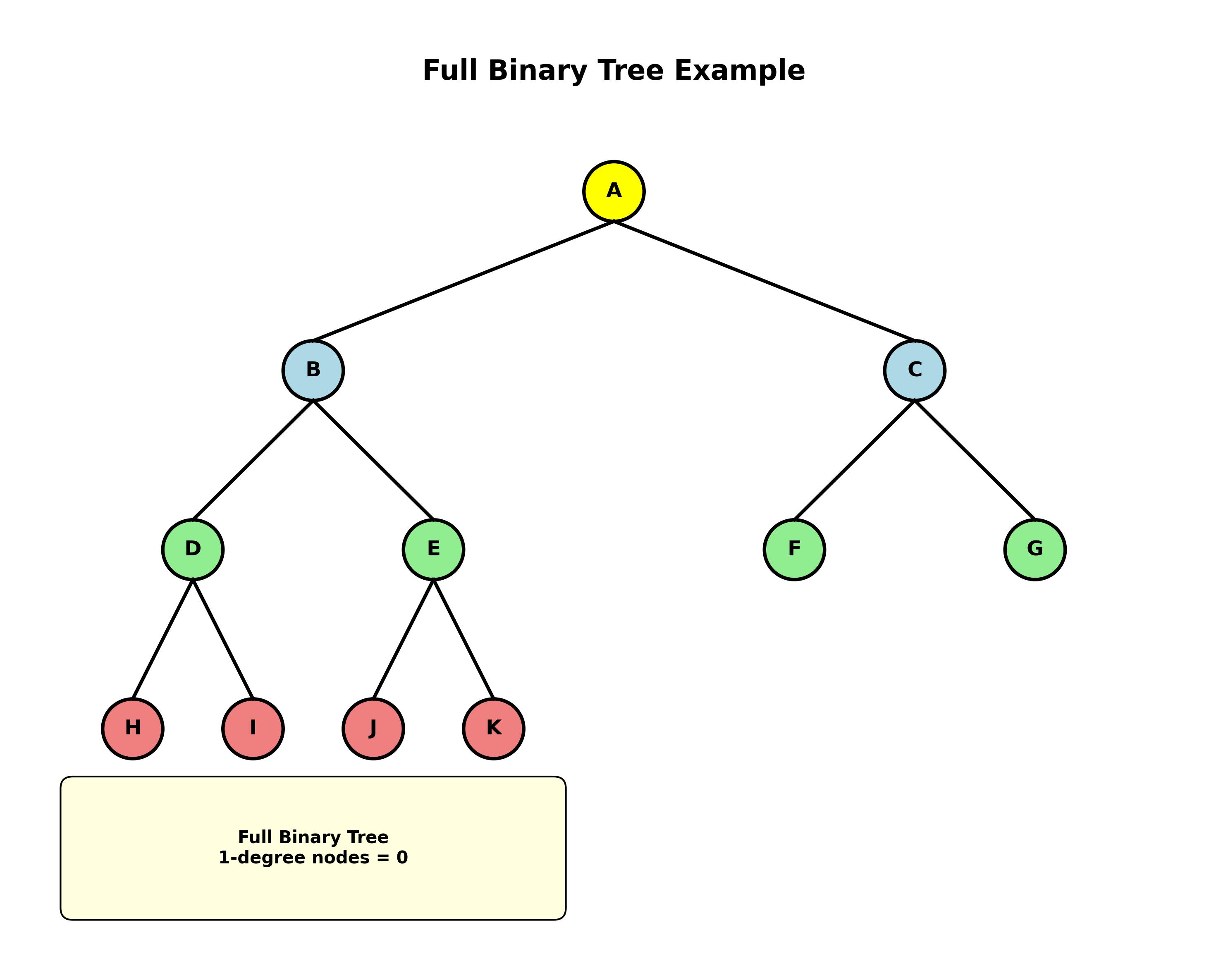
满二叉树
如果一棵二叉树的结点,或为树叶(0度节点),或为两棵非空子树(2度节点),则称作满二叉树。
特点:1度节点个数为0
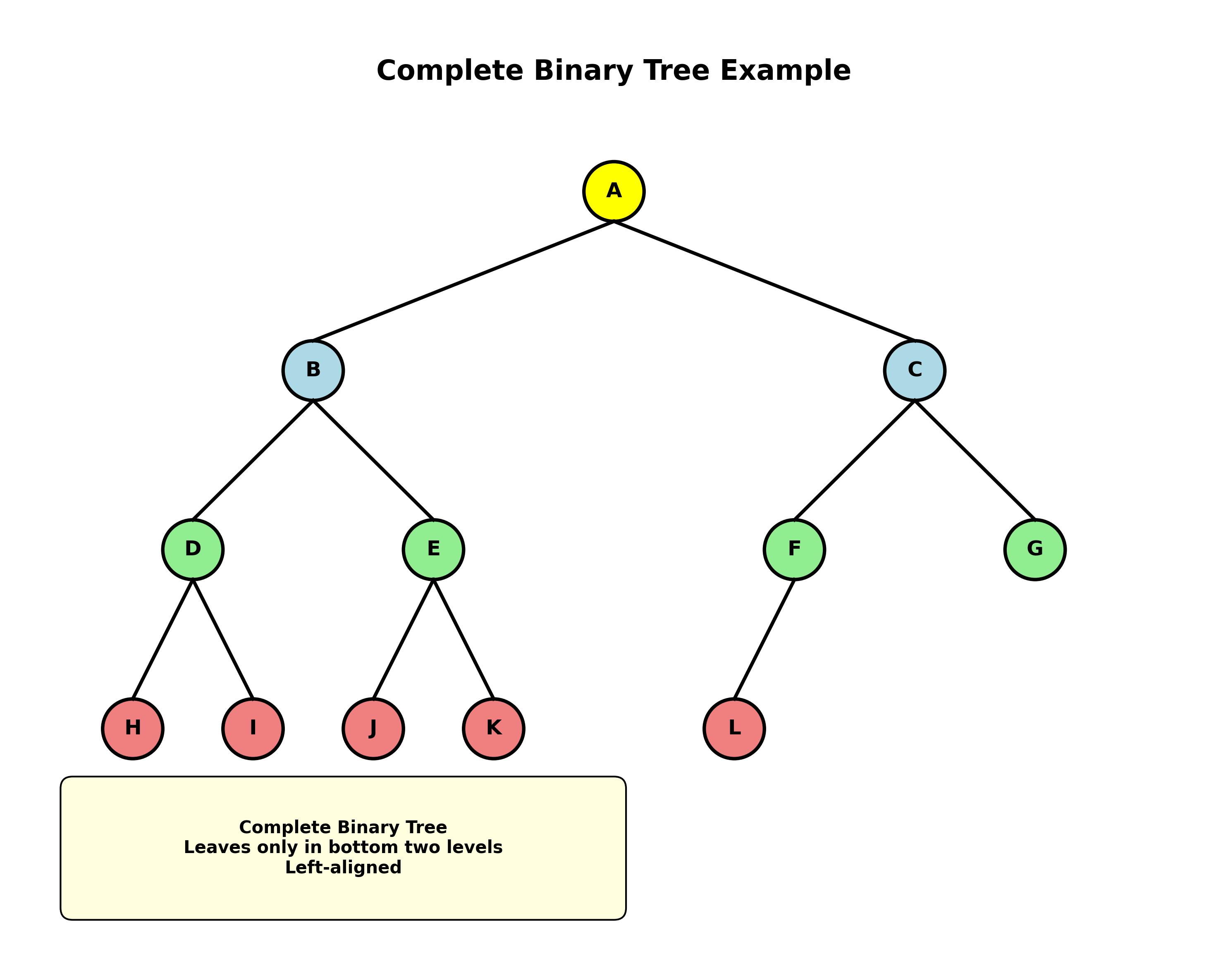
完全二叉树
若一棵二叉树:
- 最多只有最下面的两层结点度数可以小于2
- 最下面一层的结点都集中在该层最左边、连续位置上
则称此二叉树为完全二叉树。
完全二叉树的特点:
- 叶结点只可能在最下面两层出现
- 路径长度和最短(满二叉树不具有此性质)
- 由根结点到各个结点的路径长度总和在具有同样结点数的二叉树中最小
扩充二叉树
当二叉树节点出现空指针时,就增加一个特殊结点——空树叶:
- 度为1的结点,在它下面增加1个空树叶
- 度为0的树叶,在它下面增加2个空树叶
扩充的二叉树是满二叉树,新增加空树叶(外部结点)的个数等于原来二叉树结点个数(内部结点)加1。
扩充二叉树性质:
- 外部路径长度E:从扩充二叉树的根到每个外部结点的路径长度之和
- 内部路径长度I:从扩充二叉树的根到每个内部结点的路径长度之和
- E和I的关系:$E = I + 2n$,其中n是内部节点的个数
二叉树的基本性质
性质1
在非空二叉树的第i层上至多有 $2^i$ 个结点($i \geq 0$)
证明:用归纳法
- $i=0$ 时,二叉树中只有一个根结点,$2^0 = 1$ 成立
- 假定对所有的 $j (0 \leq j \leq i)$,命题成立,即第j层上至多有 $2^j$ 个结点
- 第 $i+1$ 层上的最大结点个数是第i层上最大结点个数的2倍,即 $2 \times 2^i = 2^{i+1}$
性质2
深度为k的二叉树中最多有 $2^{k+1} - 1$ 个结点($k \geq 0$)
证明: \(M = \sum_{i=0}^{k} m_i \leq \sum_{i=0}^{k} 2^i = 2^{k+1} - 1\)
性质3
对于任何一棵非空的二叉树,如果叶结点个数为 $n_0$,度为2的结点个数为 $n_2$,则有: \(n_0 = n_2 + 1\)
证明: 设二叉树中有n个结点,度为1的结点个数为 $n_1$,则:
- $n = n_0 + n_1 + n_2$ … (1)
- $B = n - 1$ (B为边的总数)… (2)
- $B = n_1 + 2n_2$ (边都是由度为1和2的结点发出)… (3)
综合(1)、(2)、(3)式可得:$n_0 = n_2 + 1$
性质4
具有n个结点的完全二叉树的深度 $k = \lfloor \log_2 n \rfloor$
性质5
对于具有n个结点的完全二叉树,如果按照从上到下和从左到右的顺序对树中的所有结点从0开始进行编号,则对于任意的序号为i的结点,有:
- 如果 $i > 0$,则其父结点的序号为 $\lfloor (i-1)/2 \rfloor$;如果 $i=0$,则其是根结点
- 如果 $2i+1 \leq n-1$,则其左子女结点的序号为 $2i+1$;否则,其没有左子女结点
- 如果 $2i+2 \leq n-1$,则其右子女结点的序号为 $2i+2$;否则,其没有右子女结点
性质6
在非空满二叉树中,叶节点的个数比分支节点的个数多1。
性质7
在扩充的二叉树里,新增加的外部结点的个数比原来的内部结点个数多1。
性质8
对任意扩充二叉树,E和I之间满足以下关系:$E = I + 2n$,其中n是内部结点个数。
二叉树的遍历
遍历定义
遍历(Traversal),也称”周游”:
- 按照一定的次序(规律)系统地访问二叉树中的结点
- 每个结点都正好被访问(输出,修改节点信息等)一次
二叉树的线性化:
- 实质是把二叉树的结点放入一个线性序列的过程
- “非线性” → “线性” 的过程
线性化方式
- 深度优先:一棵一棵子树的纵深遍历
- 广度优先:一层一层的自左而右的逐层横向遍历
深度优先遍历
变换根结点的周游顺序,可以得到以下六种方案:
前序遍历
- 访问根结点 → 前序遍历左子树 → 前序遍历右子树
- 访问根结点 → 前序遍历右子树 → 前序遍历左子树
中序遍历
- 中序遍历左子树 → 访问根结点 → 中序遍历右子树
- 中序遍历右子树 → 访问根结点 → 中序遍历左子树
后序遍历
- 后序遍历左子树 → 后序遍历右子树 → 访问根结点
- 后序遍历右子树 → 后序遍历左子树 → 访问根结点
特点:
- 根节点遍历时机的决定性
- 子树遍历结果的连续性
- 遍历过程的递归性
遍历示例
对于下图的二叉树:
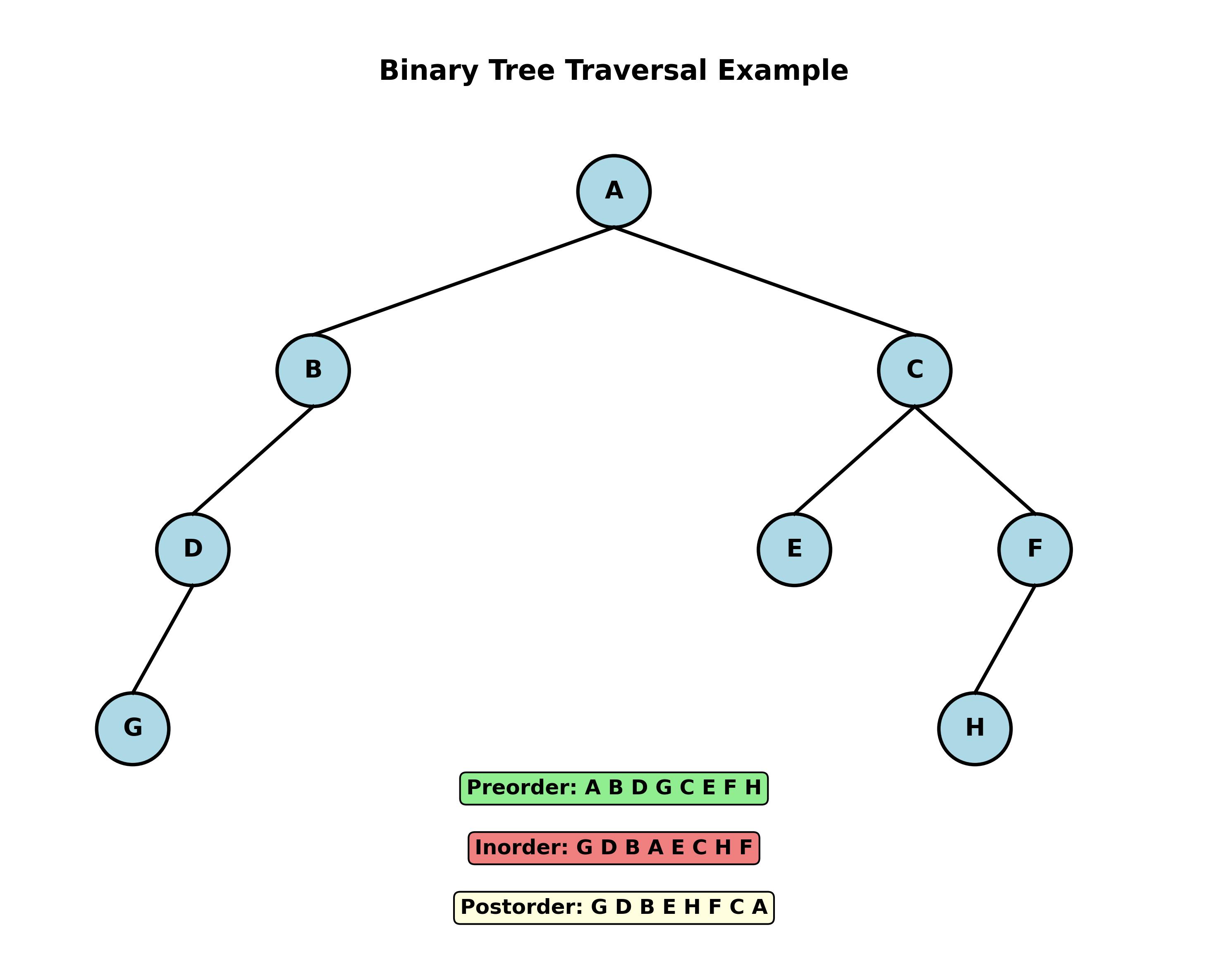
- 前序遍历:ABDGCEFH
- 中序遍历:DGBAECHF
- 后序遍历:GDBEHFCA
递归实现
template<class T>
void BinaryTree<T>::DepthOrder(BinaryTreeNode<T>* root) {
if (root != NULL) {
Visit(root); // 前序
DepthOrder(root->leftchild()); // 递归访问左子树
Visit(root); // 中序
DepthOrder(root->rightchild()); // 递归访问右子树
Visit(root); // 后序
}
}
对遍历的分析
从递归遍历算法可知:如果将Visit(root)语句抹去,从递归的角度看,这三种算法是完全相同的,或者说这三种遍历算法的访问路径是相同的,只是访问结点的时机不同。
从虚线的出发点到终点的路径上,每个结点经过3次:
- 第1次经过时访问,是先序遍历
- 第2次经过时访问,是中序遍历
- 第3次经过时访问,是后序遍历
时间复杂度:$O(n)$ (每个结点线性访问次数) 空间复杂度:$O(n)$ (栈占用的最大可能辅助空间) 精确值:树深为k的递归遍历需要k+1个辅助单元
遍历的性质
性质1
已知二叉树的先序序列和中序序列,可以唯一确定一棵二叉树。 推论:已知二叉树的后序序列和中序序列,可以唯一确定一棵二叉树。
性质2
已知二叉树的先序序列和后序序列,不能唯一确定一棵二叉树。
已知前序和中序序列求解树的方法
- 确定树的根节点:树根是当前树中所有元素在前序序列中的第一个元素
- 求解树的子树:找出根节点在中序序列中的位置,根左边的所有元素就是左子树,根右边的所有元素就是右子树
- 若根节点左边或右边为空,则该方向子树为空
- 若根节点左边和右边都为空,则根节点为叶节点
- 递归求解树:将左、右子树分别看成一棵二叉树,重复上述步骤,直到所有节点完成定位
非递归实现
递归与非递归的关系:
- 递归带来大量函数调用,有许多额外的时间开销
- 理论上所有的递归都是可以转换成非递归的
- 实现算法的非递归转换,需要借助临时的栈来实现
前序遍历非递归算法
基本思想:
- 看到一个结点,访问他,并把非空右子结点压栈,然后深度遍历其左子树
- 左子树遍历完毕,弹出结点并访问之,继续遍历
中序遍历非递归算法
基本思想:
- 遇到一个结点:入栈,遍历其左子树
- 遍历完左子树:出栈并访问之,遍历右子树
后序遍历非递归算法
基本思想:
- 遇到一个结点,将其入栈,遍历其左子树
- 左子树遍历结束后,还不能马上访问栈顶结点,而是要按照其右链去遍历其右子树
- 右子树遍历后才能从栈顶托出该结点访问之
广度优先遍历
从二叉树的根结点开始,自上而下逐层遍历;同层节点,按从左到右的顺序对结点逐一访问。
算法实现:使用队列数据结构
void BinaryTree<T>::LevelOrder(BinaryTreeNode<T>* root) {
using std::queue;
queue<BinaryTreeNode<T>*> aQueue;
BinaryTreeNode<T>* pointer = root;
if (pointer) aQueue.push(pointer);
while (!aQueue.empty()) {
pointer = aQueue.pop();
Visit(pointer->value());
if(pointer->leftchild())
aQueue.push(pointer->leftchild());
if(pointer->rightchild())
aQueue.push(pointer->rightchild());
}
}
复杂性分析:
- 时间复杂度:$O(n)$
- 空间复杂度:$O(n)$(队列占用的最大可能空间)
二叉树的存储结构
动态存储结构
二叉链表表示法
- 各结点随机存储在内存空间,结点之间关系用指针表示
- 除存储结点本身数据外,每个结点再设置两个指针字段left和right,分别指向左孩子和右孩子
- 子女为空时指针为空指针
结点形式:
| left | info | right |
三叉链表
除left和right指针外,每个结点再增加一个指向父节点的指针parent,形成”三叉链表”,提供了”向上”访问的能力。
结点形式:
| left | item | Parent | right |
静态存储结构
顺序存储(完全二叉树)
适用于完全二叉树,利用完全二叉树层次序列的规律性,使用数组进行存储。
优点:
- 不需要额外的指针空间
- 可以利用数组下标快速定位父子关系
缺点:
- 只适用于完全二叉树
- 对于一般二叉树会浪费大量空间
ADT实现
BinaryTreeNode类
template <class T>
class BinaryTreeNode {
friend class BinaryTree<T>;
private:
T info; // 二叉树结点数据域
public:
BinaryTreeNode(); // 缺省构造函数
BinaryTreeNode(const T& ele); // 给定数据的构造
BinaryTreeNode(const T& ele, BinaryTreeNode<T> *l,
BinaryTreeNode<T> *r); // 子树构造结点
T value() const; // 返回当前结点数据
BinaryTreeNode<T>* leftchild() const; // 返回左子树
BinaryTreeNode<T>* rightchild() const; // 返回右子树
void setLeftchild(BinaryTreeNode<T>*); // 设置左子树
void setRightchild(BinaryTreeNode<T>*); // 设置右子树
void setValue(const T& val); // 设置数据域
bool isLeaf() const; // 判断是否为叶结点
};
BinaryTree类
template <class T>
class BinaryTree {
private:
BinaryTreeNode<T>* root; // 二叉树根结点
public:
BinaryTree() {root = NULL;} // 构造函数
~BinaryTree() {DeleteBinaryTree(root);} // 析构函数
bool isEmpty() const; // 判定二叉树是否为空树
BinaryTreeNode<T>* Root() {return root;} // 返回根结点
void PreOrder(BinaryTreeNode<T> *root); // 前序遍历二叉树
void InOrder(BinaryTreeNode<T> *root); // 中序遍历二叉树
void PostOrder(BinaryTreeNode<T> *root); // 后序遍历二叉树
void LevelOrder(BinaryTreeNode<T> *root); // 按层次遍历二叉树
void DeleteBinaryTree(BinaryTreeNode<T> *root); // 删除二叉树
};
二叉搜索树(BST)
定义
二叉搜索树(Binary Search Tree,BST),也称二叉排序树:
- 或者是一颗空树
- 或者是具有下列性质的二叉树:
- 对于任何一个结点,设其值为K,则该结点的左子树(若不空)的任意一个结点的值都小于K
- 该结点的右子树(若不空)的任意一个结点的值都大于K
- 而且它的左右子树也分别为二叉搜索树
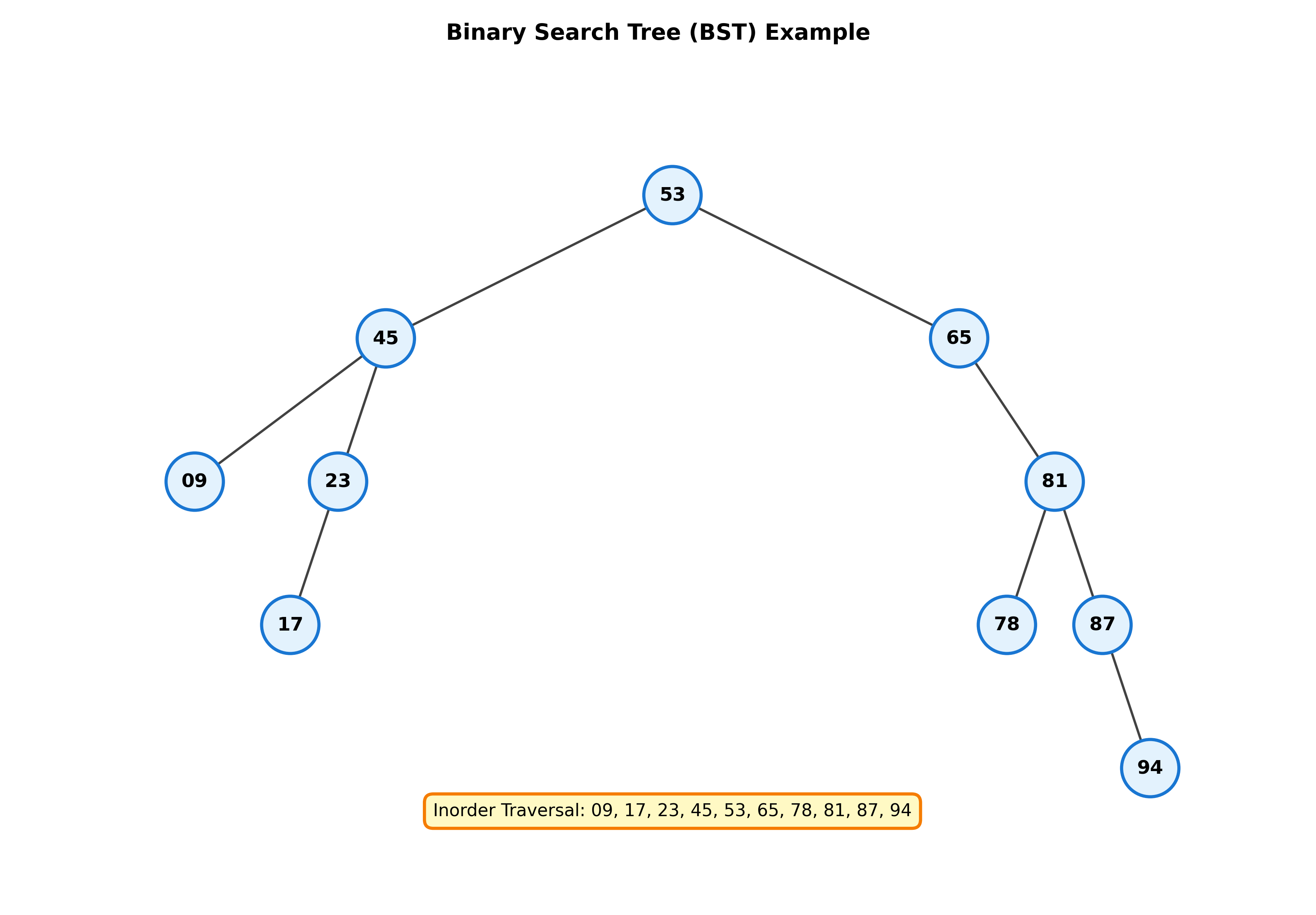
二叉搜索树的性质
- 按照中序周游将各结点打印出来,将得到由小到大的排列
- 树中结点的值唯一
搜索过程
从根结点开始,在二叉搜索树中检索值K:
- 如果根结点储存的值为K,则检索结束
- 如果K小于根结点的值,则只需检索左子树
- 如果K大于根结点的值,就只检索右子树
- 一直持续到K被找到或者遇上了一个树叶(搜索失败)
效率优势:只需检索二个子树之一
插入操作
原则:新结点插入后仍是二叉搜索树,值不重复!
插入过程:
- 将待插入结点的码值与树根的码值比较
- 若待插入的关键码值小于树根的关键码值,则进入左子树
- 否则进入右子树
- 若相等则直接返回
- 递归进行下去,直到遇到空指针,把新结点插入到该位置
注意:成功的插入,首先要执行一次失败的查找,再执行插入!
template <class T>
bool BST<T>::Insert(const T& item) {
BinaryTreeNode<T>* temp = root;
if (root == NULL) {
root = new BinaryTreeNode<T>(item);
return true;
}
while (temp != NULL) {
if (item < temp->value()) {
if (temp->leftchild() == NULL) {
temp->setLeftchild(new BinaryTreeNode<T>(item));
return true;
}
temp = temp->leftchild();
} else if (item > temp->value()) {
if (temp->rightchild() == NULL) {
temp->setRightchild(new BinaryTreeNode<T>(item));
return true;
}
temp = temp->rightchild();
} else {
return false; // 已存在
}
}
return false;
}
BST树的建立
- 对于给定的关键码集合,为建立二叉搜索树,可以从一个空的二叉搜索树开始,将关键码一个个插进去
- 将关键码集合组织成二叉搜索树,实际上起了对集合里的关键码进行排序的作用
- 按中序周游二叉搜索树,就能得到排好的关键码序列
性能分析
- BST树的检索,每次只需与结点的一棵子树比较
- 插入操作不必像在线性表中插入元素那样要移动大量的数据,而只需改动某个结点的空指针插入一个叶结点即可
- 时间复杂度是根到插入位置的路径长度,因此在树形比较平衡时二叉搜索树的效率相当高
平衡问题:
- 理想状况:插入、删除、查找时间代价为 \(O(\log n)\)
- 最坏情况(退化为链表):时间代价为 \(O(n)\)
删除操作
首先找到待删除的结点pointer,删除该结点的过程如下:
方法1(简单但可能导致不平衡):
- 若结点pointer没有左子树:则用pointer右子树的根代替被删除的结点pointer
- 若结点pointer有左子树:则在左子树里找到按中序周游的最后一个结点temppointer,把temppointer的右指针置成pointer右子树的根,然后用结点pointer左子树的根代替被删除的结点pointer
方法2(改进算法):
- 若结点pointer没有左子树:则用pointer右子树的根代替被删除的结点pointer
- 若结点pointer有左子树:则在左子树里找到按中序周游的最后一个结点replpointer(即左子树中的最大结点)并将其从二叉搜索树里删除
- 由于replpointer没有右子树,删除该结点只需用replpointer的左子树代替replpointer,然后用replpointer结点代替待删除的结点pointer
堆与优先队列
堆的定义
最小值堆:最小值堆是一个关键码序列 \(\{K_0, K_1, \ldots, K_{n-1}\}\),具有如下特性:
- \(K_i \leq K_{2i+1}\) (\(i=0, 1, \ldots, \lfloor n/2 \rfloor - 1\))
- \[K_i \leq K_{2i+2}\]
最大值堆:类似可以定义,只是将 \(\leq\) 改为 \(\geq\)
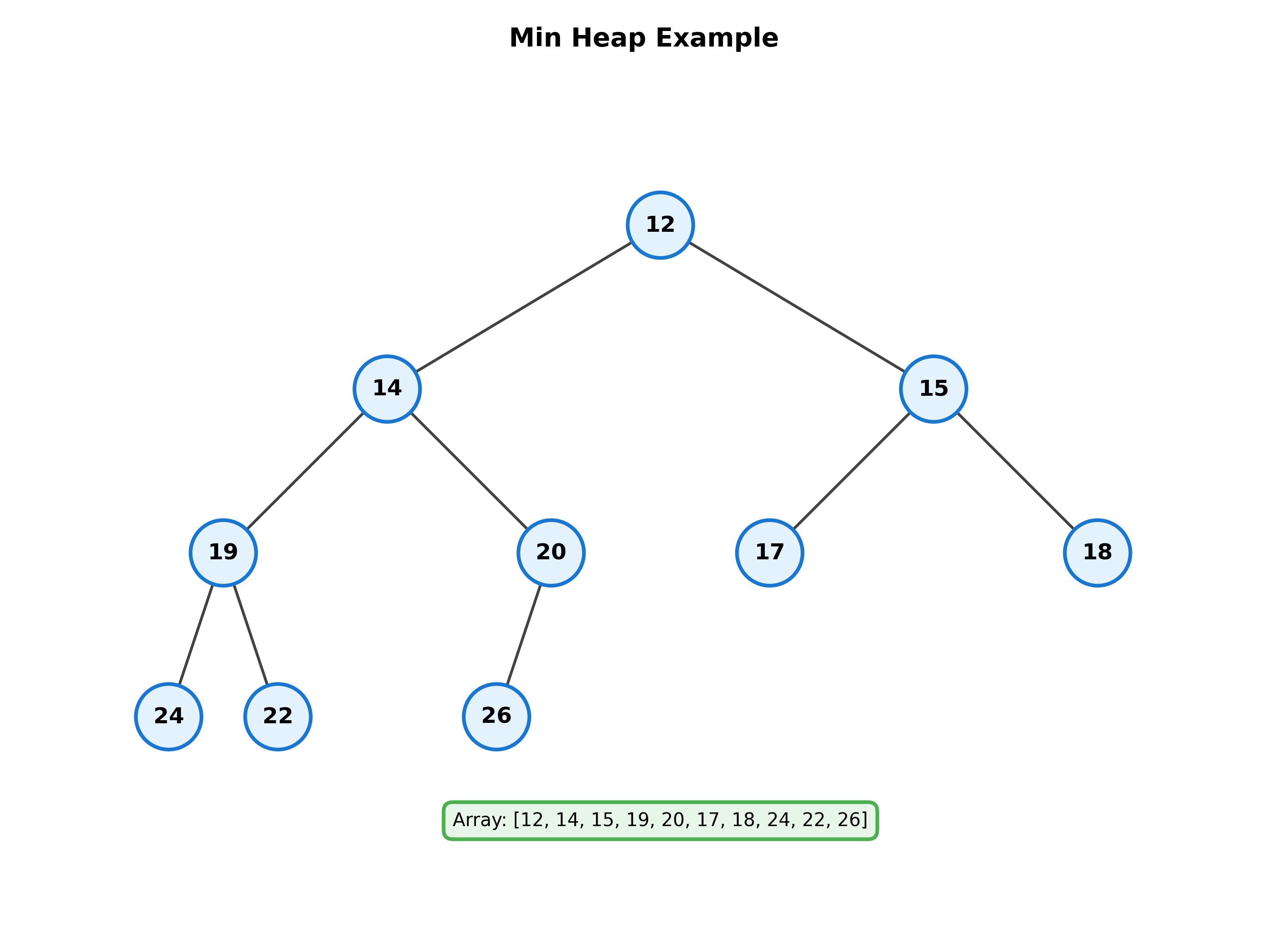
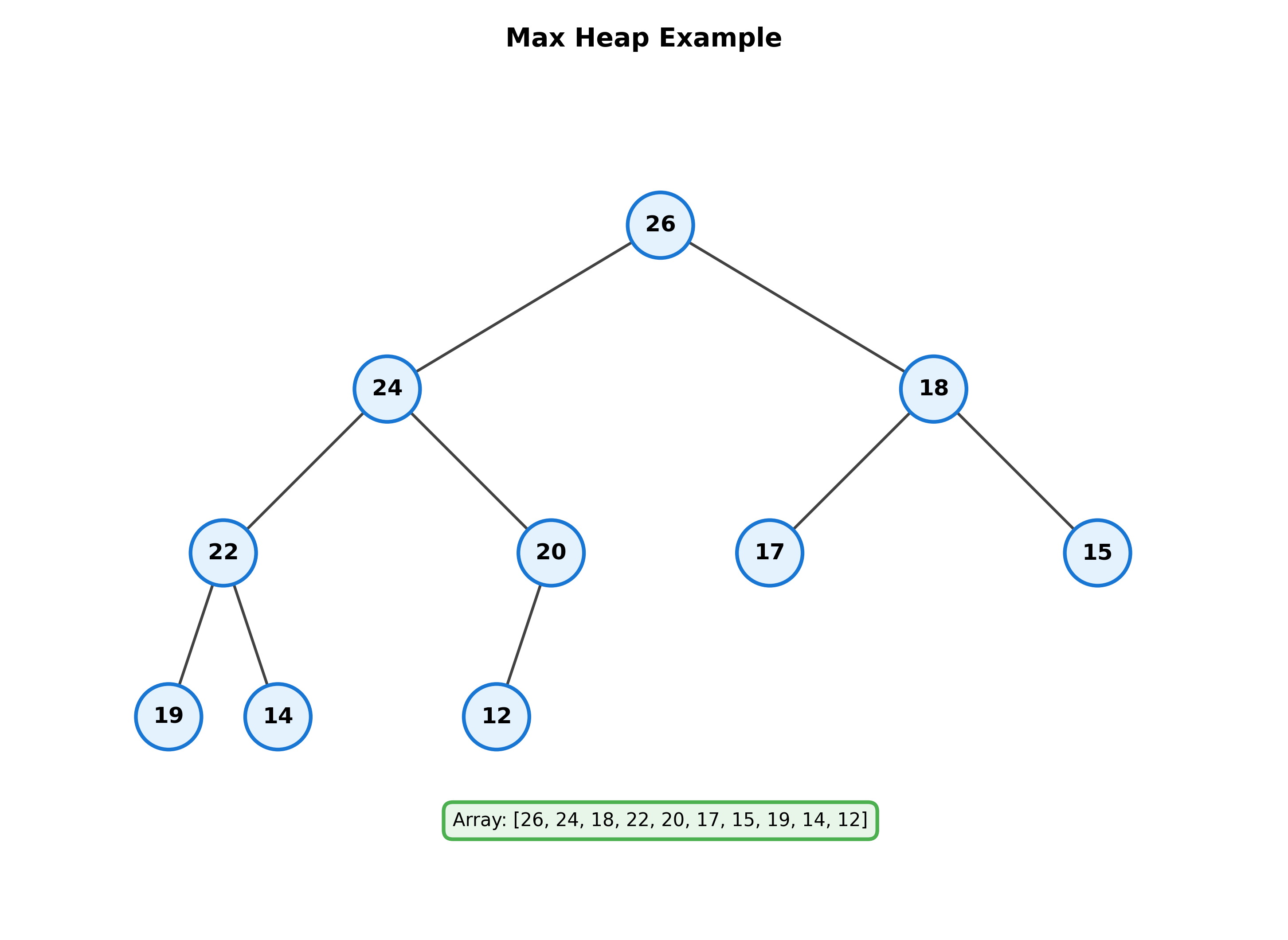
堆的性质
- 堆中储存的数据局部有序(与BST树不同)
- 结点与其子女值之间存在大小比较关系
- 两种堆(最大、最小)
- 兄弟之间没有限定大小关系
- 堆不唯一
- 从逻辑角度看,堆实际上是一种树型结构
- 堆是一个可用数组表示的完全二叉树
堆的基本操作
向下筛选(SiftDown)
用于维护堆的性质,从某个结点开始向下调整:
template <class T>
void MinHeap<T>::SiftDown(int position) {
int i = position; // 标识父结点
int j = 2*i + 1; // 标识关键码较小的子女
T temp = heapArray[i]; // 保存父结点
while (j < currentSize) {
// 让j指向两子女中,关键码较小者
if ((j < currentSize-1) && (heapArray[j] > heapArray[j+1]))
j++;
if (temp > heapArray[j]) {
heapArray[i] = heapArray[j];
i = j;
j = 2*j + 1;
} else break;
}
heapArray[i] = temp;
}
建堆
从最后一个非叶子结点开始,依次向下筛选:
template <class T>
void MinHeap<T>::BuildHeap() {
for (int i = (currentSize-2)/2; i >= 0; i--)
SiftDown(i);
}
时间复杂度:\(O(n)\)(线性时间内把一个无序序列转化成堆)
插入元素
- 将新元素放在堆的末尾
- 向上筛选调整堆
template <class T>
bool MinHeap<T>::Insert(const T& newNode) {
if (currentSize == maxSize) return false;
heapArray[currentSize] = newNode;
SiftUp(currentSize);
currentSize++;
return true;
}
删除最小值
- 用堆的最后一个元素替换根结点
- 向下筛选调整堆
template <class T>
bool MinHeap<T>::RemoveMin(T& node) {
if (currentSize == 0) return false;
node = heapArray[0];
heapArray[0] = heapArray[currentSize-1];
currentSize--;
if (currentSize > 1)
SiftDown(0);
return true;
}
复杂度分析
- 建堆:\(O(n)\)
- 插入、删除:平均和最差时间代价都是 \(O(\log n)\)
优先队列
优先队列(Priority Queue)是0个或多个元素的集合,每个元素有一个关键码值,执行查找、插入和删除操作。
主要特点:从一个集合中快速地查找并移出具有最大值或最小值的元素。
- 最小优先队列:适合查找和删除最小元素
- 最大优先队列:适合查找和删除最大元素
堆是优先队列的一种自然的实现方法
Huffman树及其应用
Huffman编码树
带权外部路径长度
一个具有n个外部结点的扩充二叉树:
- 每个外部结点 \(K_i\) 有一个 \(w_i\) 与之对应,称为该外部结点的权
- 带权外部路径长度:二叉树叶结点带权外部路径长度总和
其中 \(l_i\) 为第i个外部结点的路径长度
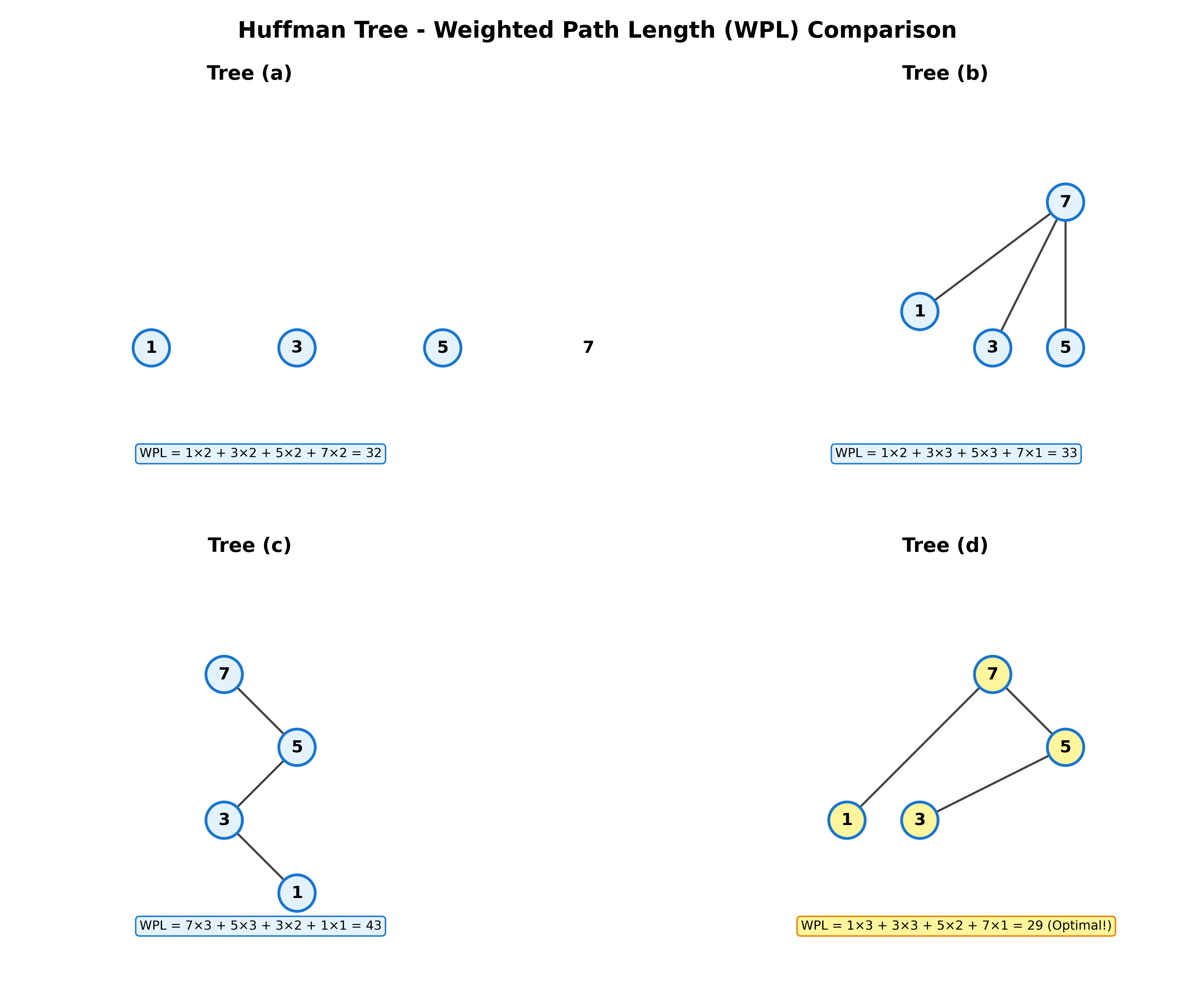
Huffman树定义:具有最小带权路径长度的二叉树称作Huffman树(或称最优二叉树)
建立Huffman编码树
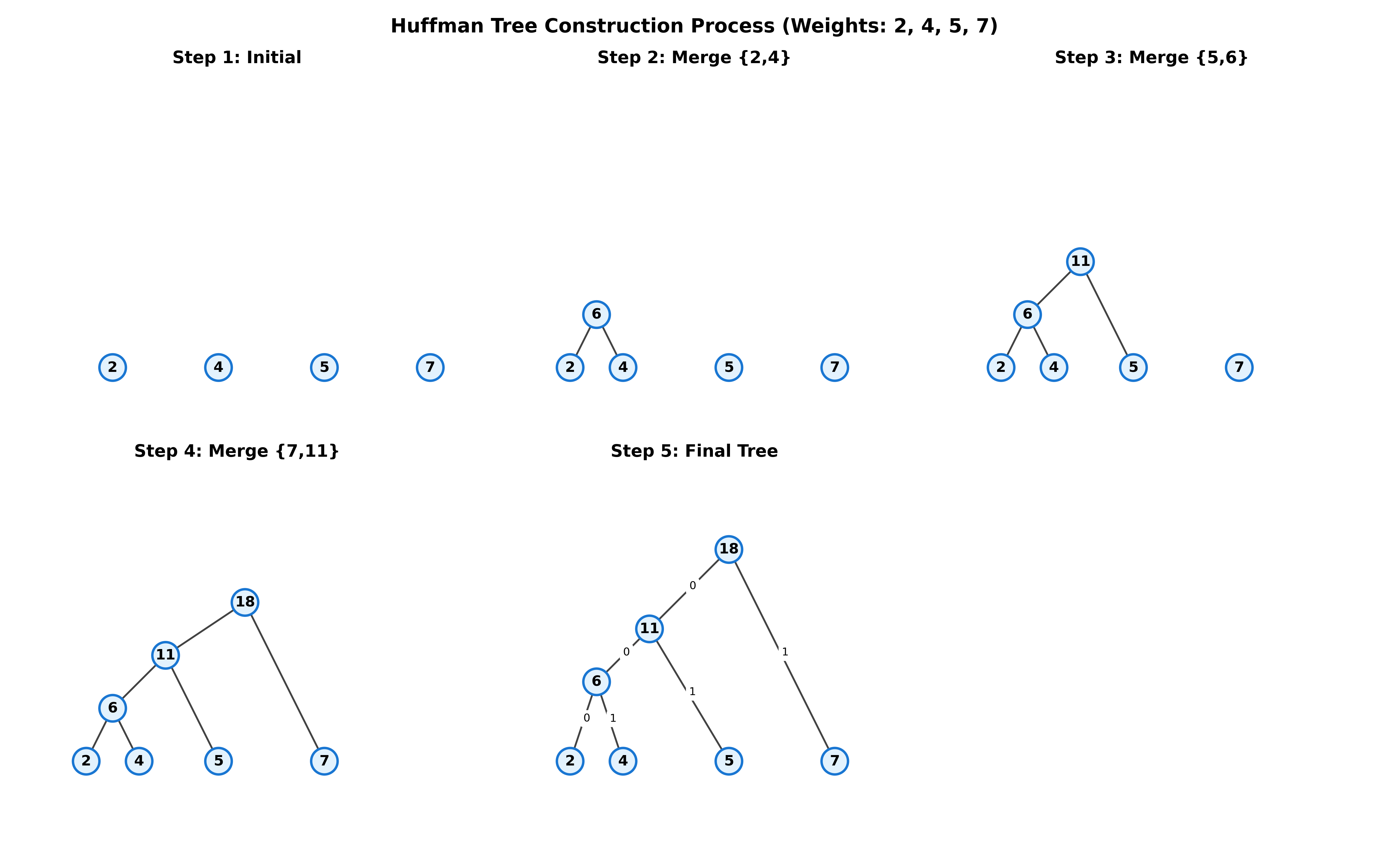
算法步骤:
- 首先,按照”权重”(例如频率)将字母排为一个有序序列
- 接着,拿走前两个字母(”权”最小的两个字母),再将它们标记为Huffman树的树叶,将这两个树叶标为一个分支结点的两个子女,而该结点的权即为两树叶的权之和
- 将所得”权”放回序列中适当位置,使”权”的顺序保持
- 重复上述步骤直至序列中剩一个元素,则Huffman树建立完毕
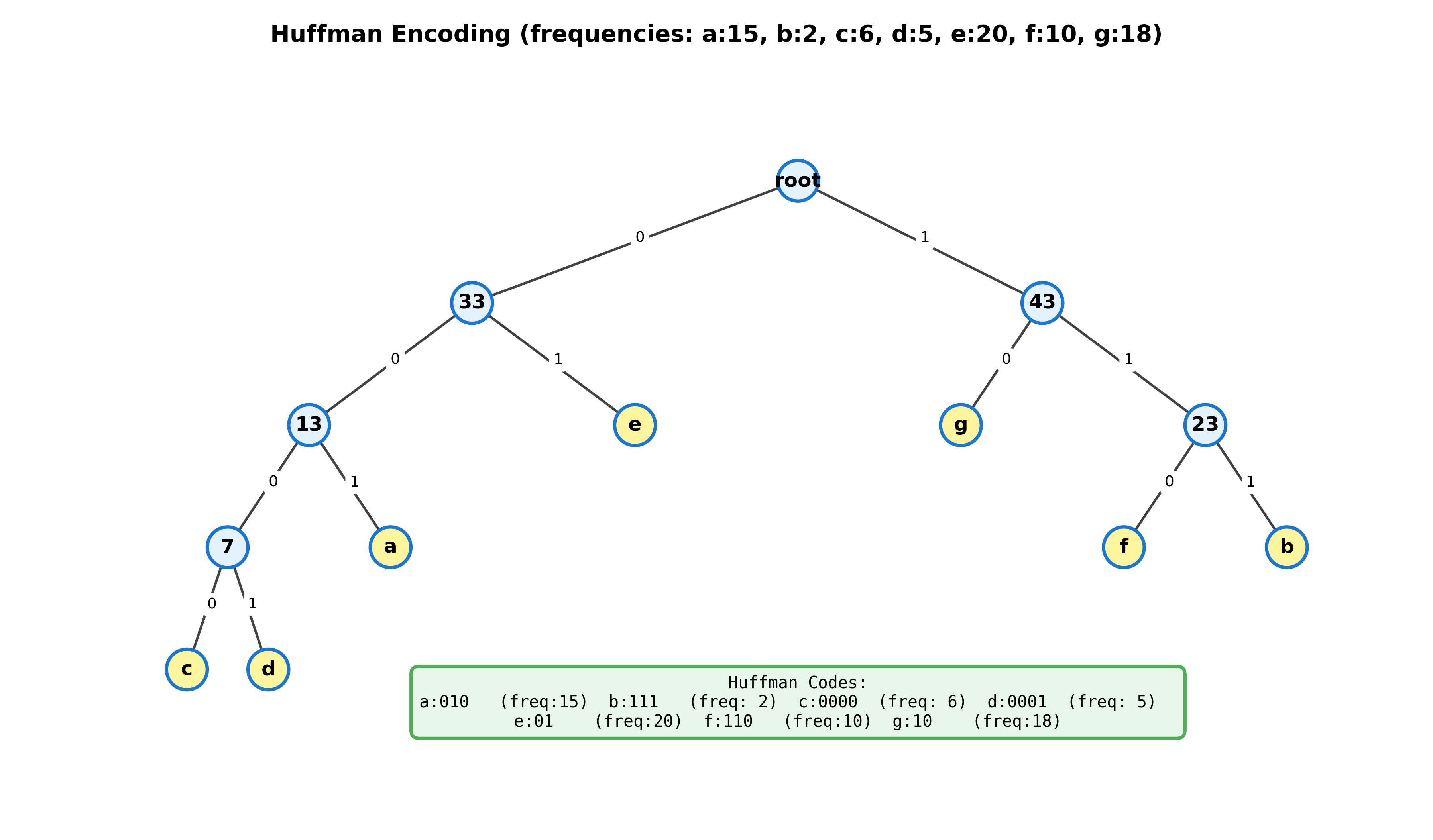
Huffman编码
Huffman树的一个重要应用是解决数据通信中的二进制编码问题。
设 \(D = \{d_0, \ldots, d_{n-1}\}\),\(W = \{w_0, \ldots, w_{n-1}\}\)
- D为需要编码的字符集合
- W为D中各字符出现的频率
要对D里的字符进行二进制编码,使得:\(\sum_{i=0}^{n-1} w_i l_i\) 最小
其中,\(l_i\) 为第i个字符的二进制编码长度。
设计电文总长度最短的编码问题就转化成了设计字符出现频率作为外部结点权值的Huffman树的问题。
Huffman编码性质
- 不等长编码:代码长度取决于对应字符的相对使用频率或”权重”
- 前缀特性:任何一个字符的编码都不是另一个字符编码的前缀
- 前缀特性保证了代码串被反编码时,不会有多种可能
编码与译码
编码过程:
- 从根结点到叶结点的路径
- 左分支标记为0,右分支标记为1
- 路径上的0、1序列即为该字符的编码
译码过程:
- 从二叉树的根开始,把二进制编码每一位的值与Huffman树边上标记的0、1相匹配
- 确定选择左分支还是右分支,直至确定一条到达树叶的路径
- 一旦到达树叶,就译出了一个字符
- 然后继续用这棵二叉树继续译出其它二进制编码
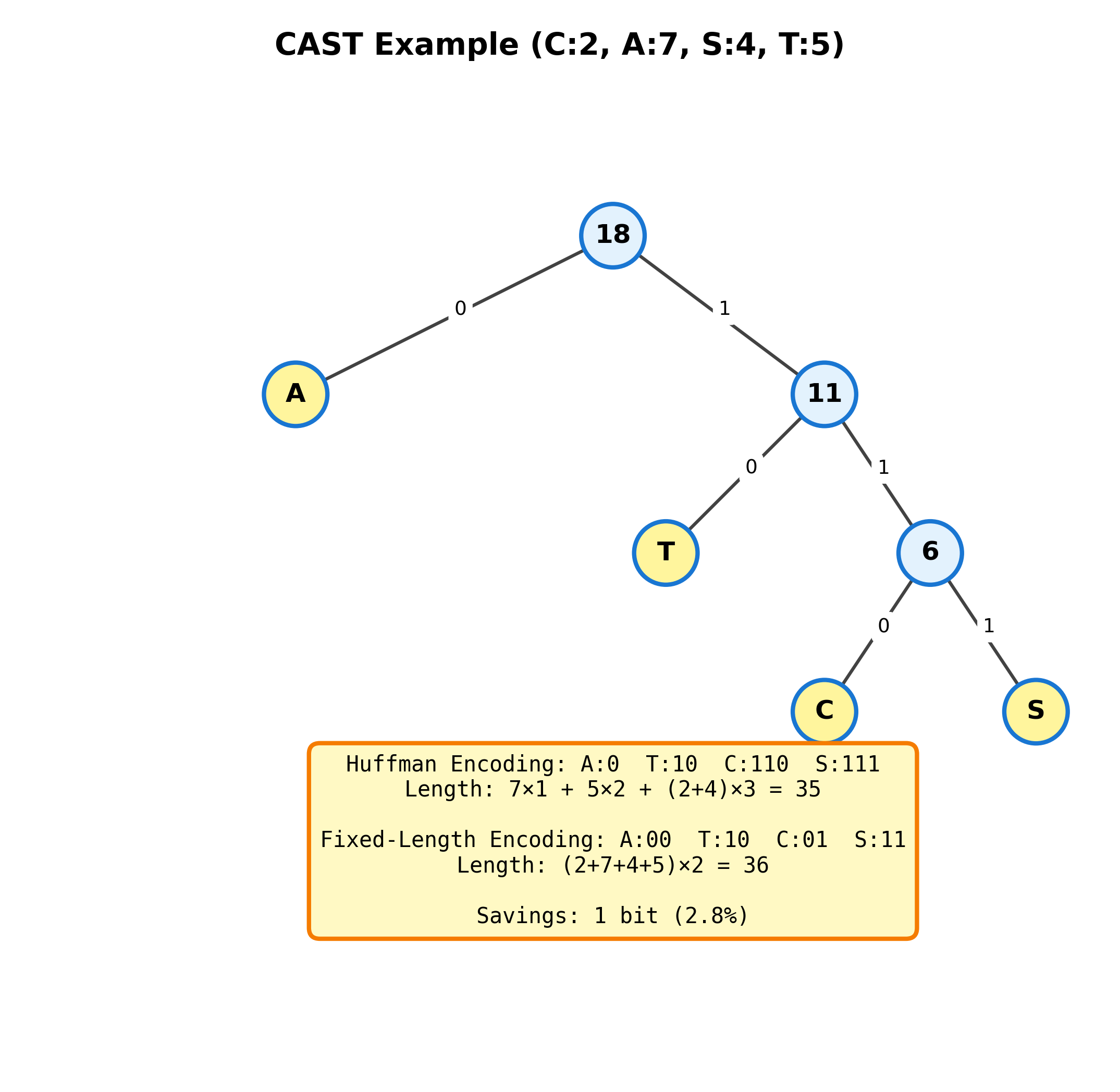
示例:CAST
字符集合:\(\{C, A, S, T\}\) 出现频度:\(W = \{2, 7, 4, 5\}\)
等长编码:
- A: 00, T: 10, C: 01, S: 11
- 总编码长度:\((2+7+4+5) \times 2 = 36\)
Huffman编码:
- A: 0, T: 10, C: 110, S: 111
- 总编码长度:\(7 \times 1 + 5 \times 2 + (2+4) \times 3 = 35\)
编码比较:
- Huffman编码:
110011110 11001111011101001001001110 - 等长编码:
010011100100111011001000100010001100
本章小结
主要内容
-
定义和性质
- 二叉树的递归定义
- 8条基本性质
- 满二叉树、完全二叉树、扩充二叉树
-
存储结构
- 顺序结构(完全二叉树)
- 链式结构(二叉链表、三叉链表)
-
遍历
- 深度优先(前序、中序、后序)
- 广度优先(层次遍历)
- 递归与非递归实现
-
二叉搜索树
- 搜索、插入、删除操作
- 平衡问题
-
堆与优先队列
- 最小堆、最大堆
- 建堆、插入、删除操作
- 优先队列的实现
-
Huffman树及应用
- Huffman编码
- 数据压缩应用
思考题
-
在具有n(n≥1)个结点的k叉树中,有n(k-1)+1个指针是空的。
-
给定一个入栈序列,序列长度为N,有多少种出栈序列? 答案:卡特兰数 \(C_n = \frac{(2n)!}{n!(n+1)!}\)
本笔记基于北京大学《数据结构与算法》第五章内容整理
Enjoy Reading This Article?
Here are some more articles you might like to read next: