数据结构与算法 - 第4章: 字符串

4.1 字符串的基本概念

字符串定义

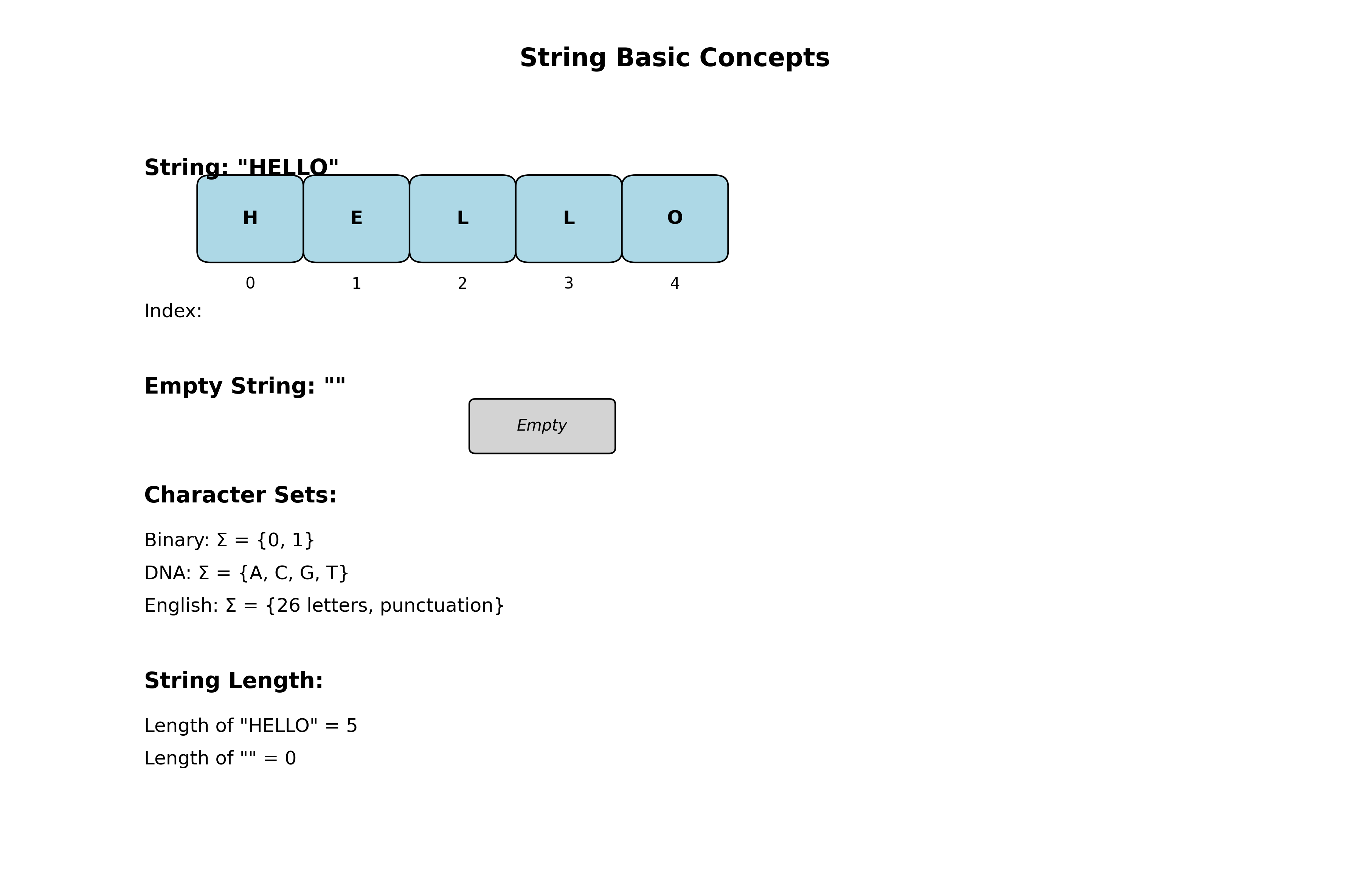
字符串（String）：由0或多个字符顺序排列所组成的有限序列，简称”串”
串长度：字符串所包含的字符个数
空串：长度为零的串""；空格串：" "
字符串常数：一般用一对双引号""括起来，如”SUNDAY”、”123”、”字符串”等

字符与字符编码

字符(char)：组成字符串的基本单位，取值依赖于字符集$\Sigma$
- 二进制字符集：$\Sigma = \{0,1\}$
- 生物信息中DNA字符集：$\Sigma = \{A,C,G,T\}$
- 英语语言：$\Sigma = \{26个字符，标点符号\}$
字符编码
- 字符类型是单字节（8 bits）类型
- 采用ASCII码对128个符号（字符集charset）进行编码
- 国标编码GB2312（两个字节）、通用文字符号编码标准UNICODE

字符串比较

偏序编码规则：字符编码表一般遵循”偏序编码规则”，便于字符串间比较
字符偏序：根据字符的自然含义，某些字符间两两可以比较次序
字典序：大多数情况下就是字典序（中文字符串有特例，如”笔划”序）

例如：encode('0')+1=encode('1')，"monday"<"sunday"

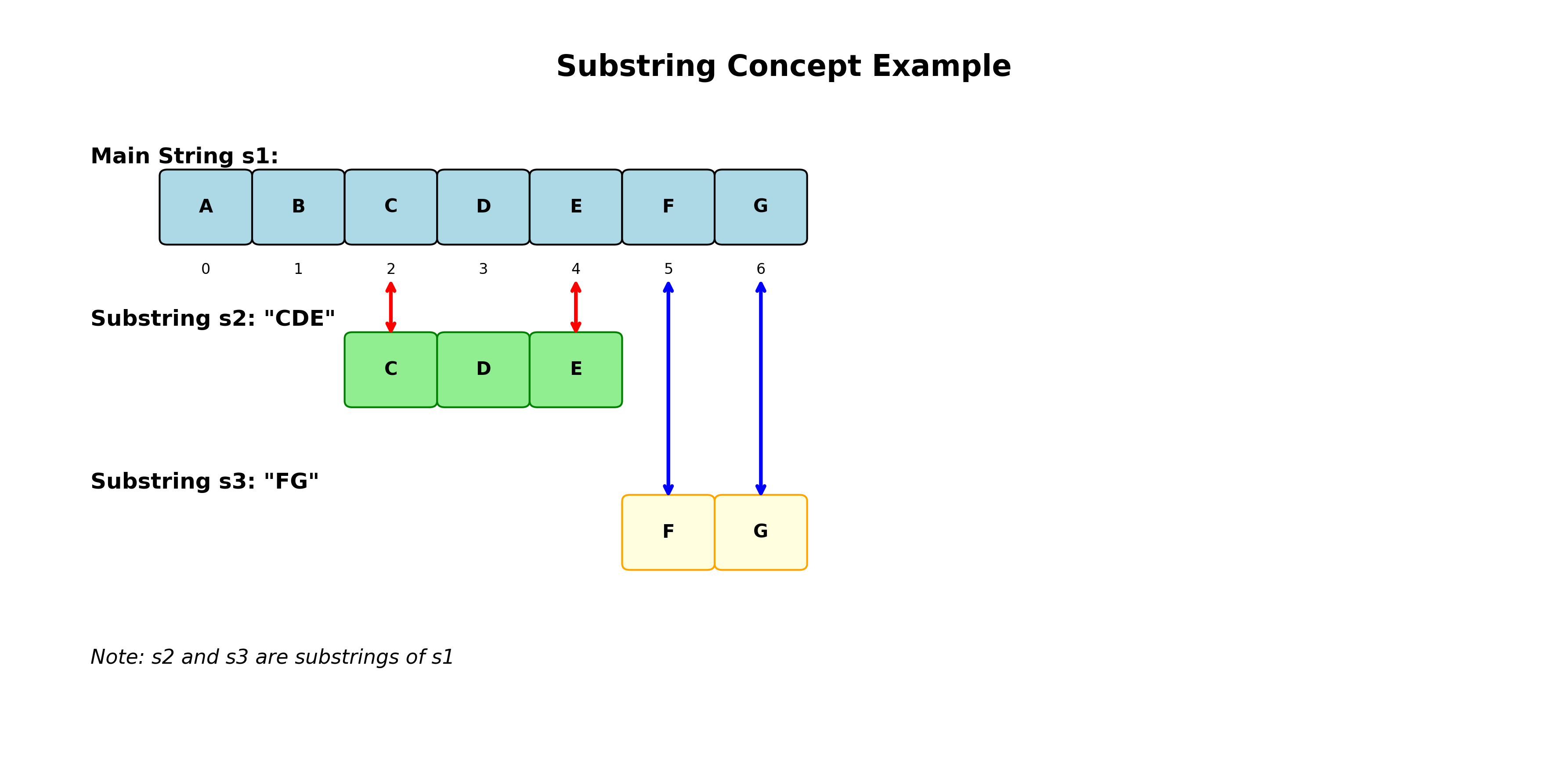
子串概念

假设$s_1, s_2$是两个串：

$s_1 = a_0a_1a_2\ldots a_{n-1}$和$s_2 = b_0b_1b_2\ldots b_{m-1}$，$(0 \leq m \leq n)$
若存在整数$i$ $(0 \leq i \leq n-m)$，使得$b_j = a_{i+j}, j = 0,1,\ldots,m-1$同时成立，则称串$s_2$是串$s_1$的子串，或称$s_1$包含串$s_2$
真子串：非空且不为自身的子串（空串是任意串的子串）
任意串$S$都是$S$本身的子串

思考题：若字符串s="software"，则其子串（真子串）的数目为多少？答案：37（35）

4.2 字符串的存储结构与实现

字符串的复杂性

字符串的复杂性源于其长度的动态变化

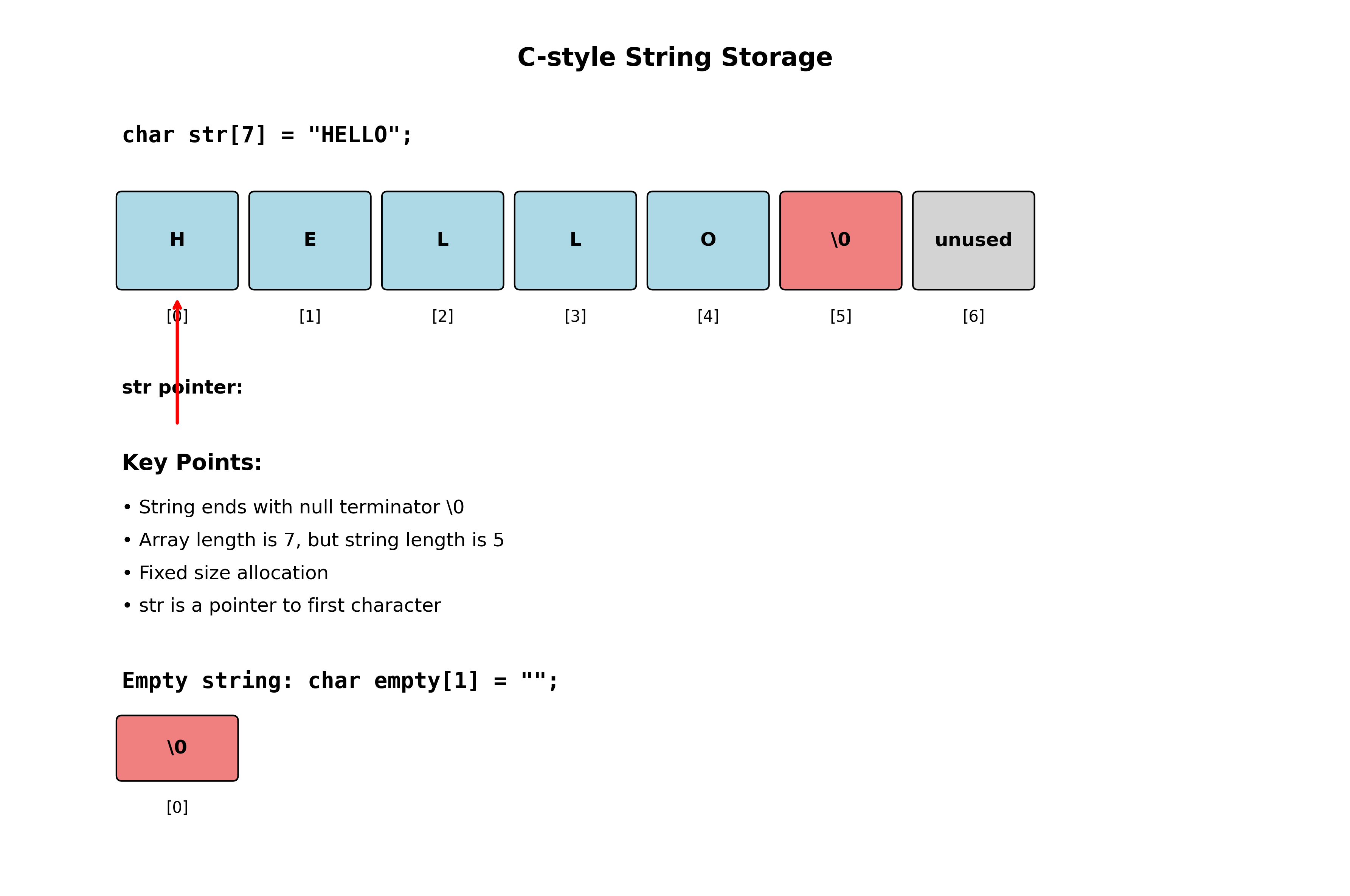
静态存储：C++标准字符串

标准字符串：采用char S[M]的形式定义字符串变量
$M$是常量，保持不变
串的结束标记：'\0'（ASCII码中8位BIT全0码，又称为NULL）
长度为$M$的字符串实际最大容量为$(M-1)$

char s1[7]="value.";
char s2[9];

s1,s2实际上就是指向字符串首地址的指针，拷贝赋值需要一位一位的来做：s1[i]=s2[i]

标准字符串函数

// 串长函数 - 返回字符串s的长度
int strlen(char *s);

// 串复制 - 将s2值复制给s1，返回指针指向s1
char *strcpy(char *s1, char *s2);

// 串拼接 - 将串s2拼接到s1的尾部
char *strcat(char *s1, char *s2);

// 串比较
int strcmp(char *s1, char *s2); // (=, >, <)

// (左)定位函数 - c在s中第一次出现的位置
char *strchr(char *s, char c);

// 右定位函数 - 逆向寻找c在s中第一次出现的位置
char *strrchr(char *s, char c);

动态存储：字符串类

字符串类（class String）适应字符串长度动态变化的复杂性，采用动态变长的存储结构。

class string {
private: // 字符串的存储结构在具体实现时定义
    char *str;    // 字符串的数据表示
    int size;     // 串的当前长度
public: // 字符串的运算集
    string(char *s = "");     // 创建一个空字符串
    string(char *s);          // 创建一个初值为s的字符串
    ~string();                // 消除该串实例
    int length();             // 返回串的长度
    int isEmpty();            // 判断串是否为空串
    void clear();             // 把串清空
    string append(char c);    // 在串尾添加字符
    string concatenate(char *s); // 把串s连接在本串后面
    string copy(char*s);      // 将一个串s拷贝到本串
    string insert(char c, int index); // 往串中给定位置插字符
    int find(char c, int start);       // 从位置start开始搜索串寻找一个给定字符
    string substr(int s, int len);     // 从位置s开始提取一个长度为len的子串
};

4.3 字符串的模式匹配

模式匹配的定义

模式匹配（Pattern Matching）：

一个目标对象$T$（字符串）
一个模板（pattern）$P$（字符串）
任务：用给定的模板$P$，在目标字符串$T$中搜索与模板$P$全相同的一个子串，并返回$P$和$T$匹配的第一个子串的首字符位置

示例：$T="easdknjeasdk"$，$P="asdk"$，返回1

模式匹配的意义

是计算机科学中最古老、研究最广泛的问题之一
有着大量的实际应用：生物信息学、信息检索、拼写检查、数据压缩检测等
大数据的搜索代价不容小觑！

朴素模式匹配算法

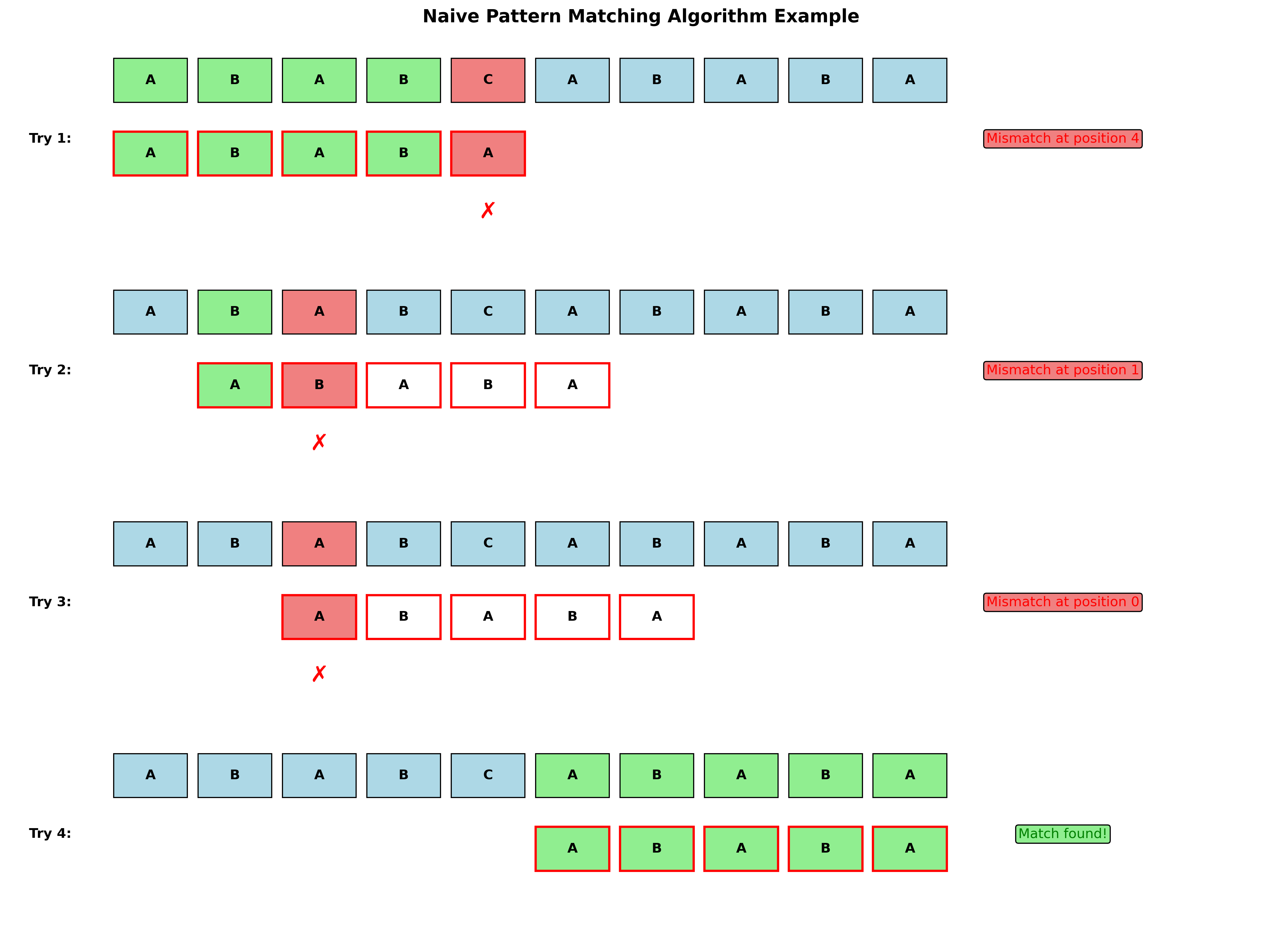
设$T= t_0t_1, t_2, \ldots,t_{n-1}$，$P = p_0, p_1, \ldots, p_{m-1}$

$i$为$T$中字符的下标，$j$为$P$中字符的下标
匹配成功：$(p_0 = t_i, p_1 = t_{i+1}, \ldots, p_{m-1} = t_{i+m-1})$ 即，$T.substr(i, m) == P.substr(0, m)$
匹配失败：$(p_j \neq t_i)$时，将$P$右移再行比较，尝试所有的可能情况

朴素匹配算法实现

int FindPat_3(string T, string P, int startindex) {
    // g为T的游标，j为P的游标
    for (int g = startindex; g <= T.length() - P.length(); g++) {
        for (int j=0; ((j<P.length()) && (T[g+j]==P[j])); j++);
        if (j == P.length())
            return g;
    }
    return(-1); // for结束，或startindex值过大,则匹配失败
}

朴素匹配算法性能分析

最佳情况：$O(M)$ - 在目标的前$M$个位置上找到模式
最差情况：$O(M \times N)$ - 目标形如$a^n$，模式形如$a^{m-1}b$ 总比较次数：$M(N-M+1)$

KMP算法

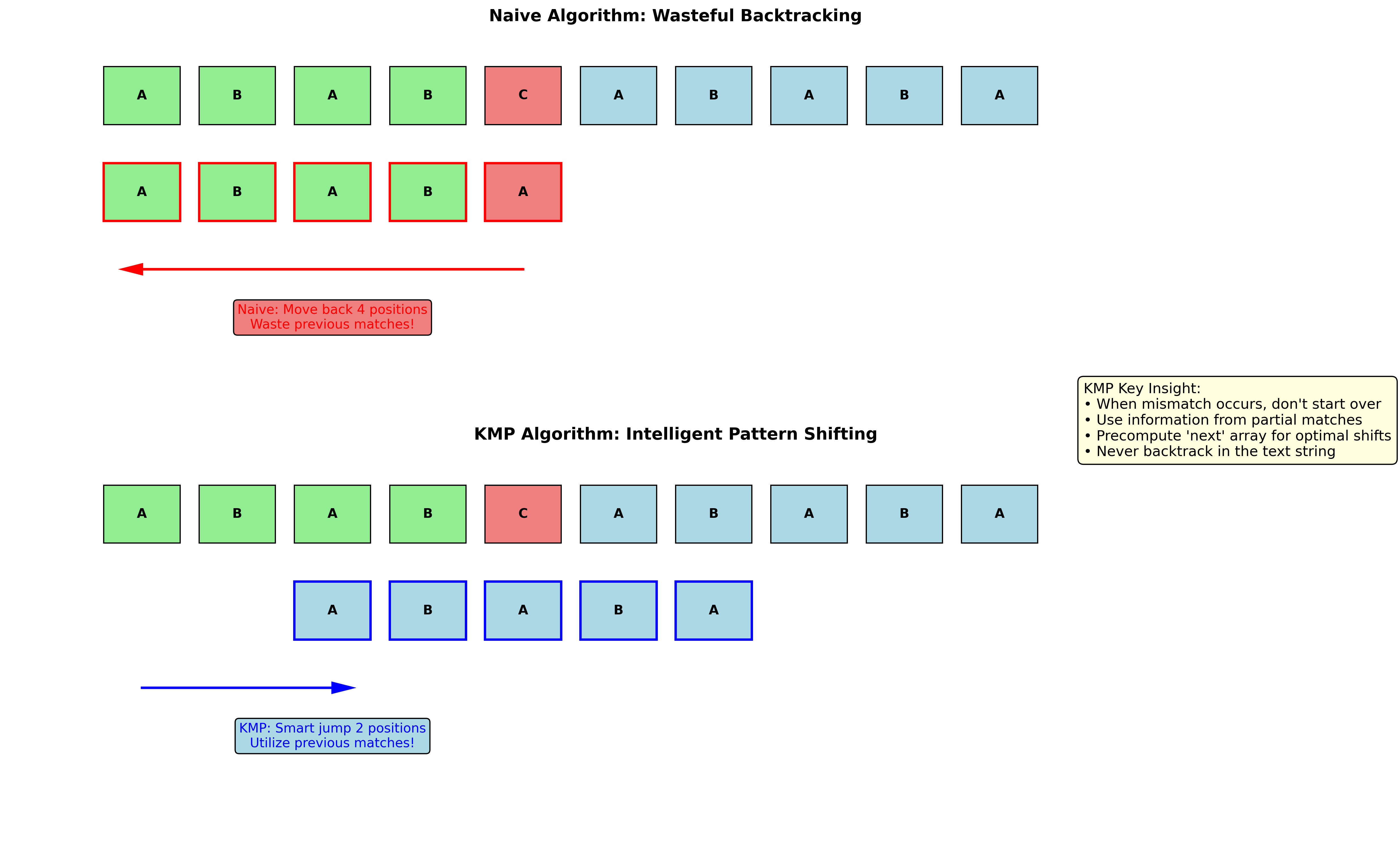
KMP算法思想

Knuth-Morris-Pratt (KMP)算法发现，$P$中每个字符对应一个移位值$k$，该值仅依赖于模式$P$本身，与目标$T$无关。

核心思想：如何利用匹配失败位置前的信息，消除大量不必要的回溯？

当$P_i \neq T_j$时： $T_{j-i}T_{j-i+1}T_{j-i+2} \ldots T_{j-1} = P_0P_1P_2 \ldots P_{i-1}$

寻找最长的（$k$最大的）能够与前缀子串匹配的后缀子串： $P_0P_1\ldots P_{k-1} = P_{i-k}P_{i-k+1}\ldots P_{i-1}$

特征向量N（Next数组）

设模板$P$由$m$个字符组成：$P = p_0p_1p_2p_3\ldots p_{m-1}$

特征向量$N$用来表示模板$P$的字符分布特征： $N = n_0 n_1 n_2 n_3 \ldots n_{m-1}$

特征数$n_i$的递归定义：

$n_0 \leftarrow -1$，对于$i > 0$的$n_i$，假定已知前一位置的特征数$n_{i-1}$，并且$n_{i-1} = k$
如果$p_i = p_k$，则$n_{i+1} \leftarrow k + 1$
当$p_i \neq p_k$且$k \neq 0$时，则令$k \leftarrow n_k$，循环直到条件不满足
当$p_i \neq p_k$且$k = 0$时，则$n_{i+1} = 0$

数学表达式：

\[next[i] = \begin{cases} -1, & \text{对于 } i = 0 \\ \max\{k: 0 < k < i \text{ \&\& } P(0...k-1) = P(i-k...i-1)\}, & \text{如果k存在} \\ 0, & \text{否则} \end{cases}\]

Next数组计算算法

int findNext(string P) {
    int i, k;
    int m = P.length();     // m为模板P的长度
    int *next = new int[m]; // 动态存储区开辟整数数组
    next[0] = -1;
    i = 0; k = -1;
    while (i < m-1) {       // 若写成i < m 会越界
        // 如果不等，采用KMP方法自找首尾子串
        while (k >= 0 && P[k] != P[i])
            k = next[k];    // k递归地向前找
        i++; k++;
        next[i] = k;
    }
    return next;
}

KMP匹配算法

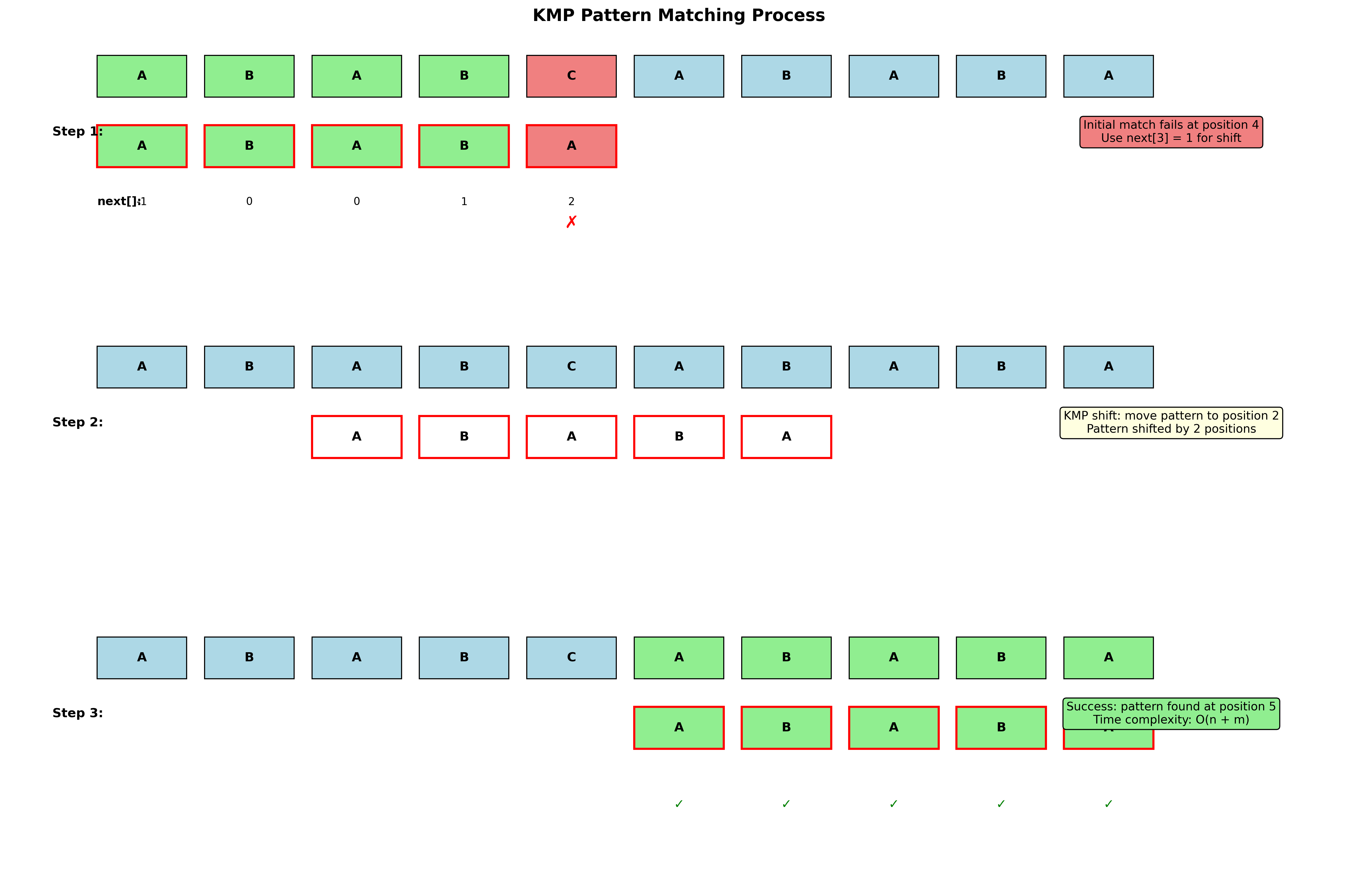
实现

int KMPStrMatching(string T, string P, int *N, int start) {
    int i = 0;              // 模式的下标变量
    int j = start;          // 目标的下标变量
    int pLen = P.length();  // 模式的长度
    int tLen = T.length();  // 目标的长度
    if (tLen - start < pLen) // 若目标比模式短，匹配无法成功
        return (-1);
    while (i < pLen && j < tLen) { // 反复比较对应字符来开始匹配
        if (i == -1 || T[j] == P[i])
            i++, j++;
        else
            i = Next[i];
    }
    if (i >= pLen)
        return (j-pLen+1);
    else
        return -1;
}

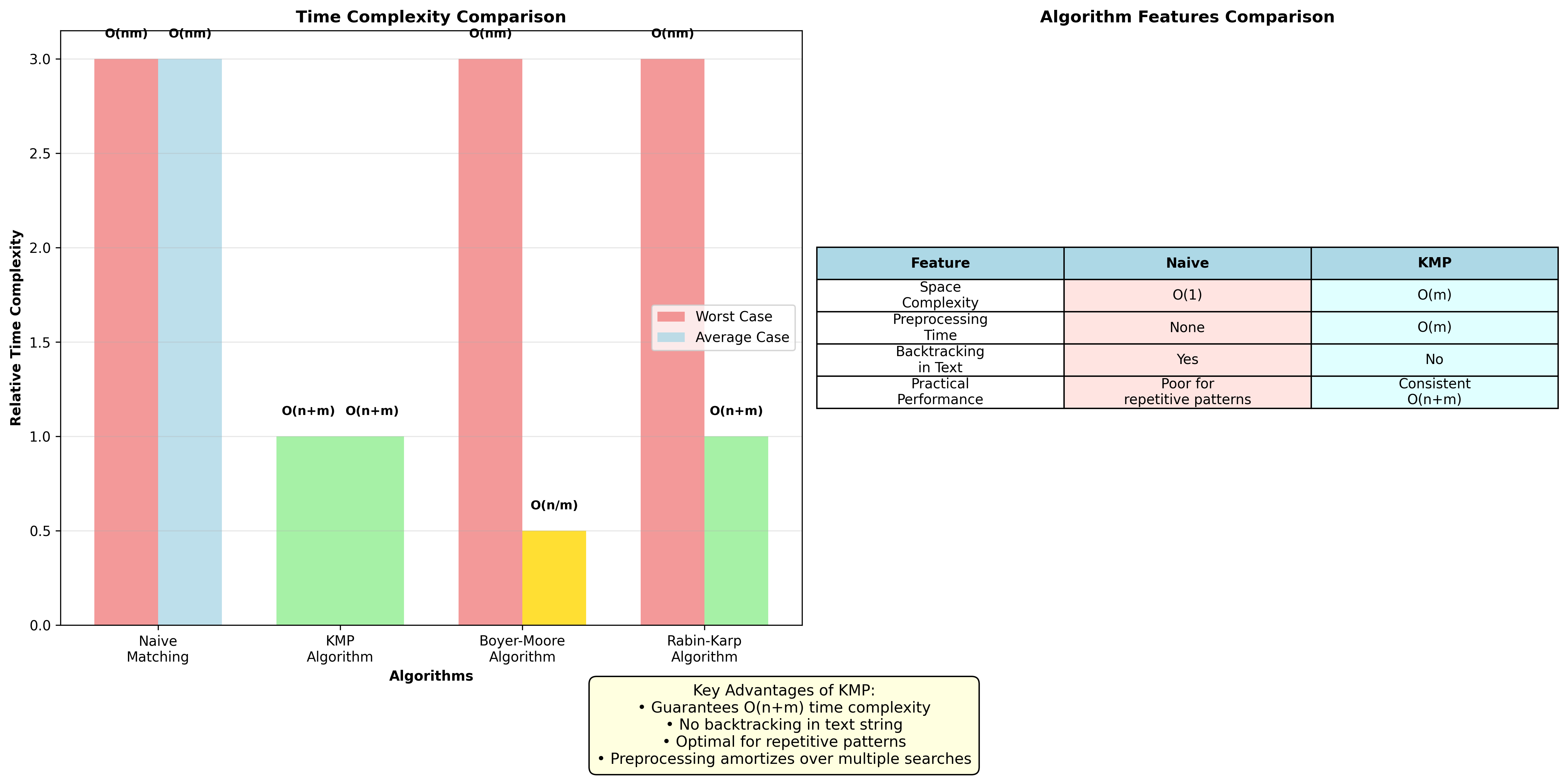
KMP算法效率分析

时间复杂度：$O(n+m)$
while循环语句中，$j$只增不减，所以循环体中的$j++$语句执行次数最多$$ N $$次
$i$的初值为0，使之减少的语句只有$i = N[i]$，循环体中$i = N[i]$的执行次数不会超过$i++, j++$语句的执行次数加1
整个循环体的执行次数至多为$$2 N +1$$次，时间代价与目标串的长度成线性关系
求next数组的时间为$O(m)$
因此，KMP算法的时间为$O(n+m)$

Next数组优化

当$P[k] == P[i]$时，优化算法：

if (P[k] == P[i])
    next[i] = next[k];  // 前面找k值，优化步骤
else
    next[i] = k;

总结

字符串抽象数据类型
字符串的存储结构和类定义
字符串运算的算法实现
字符串的模式匹配
- 特征向量N及相应的KMP算法还有其他变种、优化