数据结构与算法 - 3: 栈与队列

Created on September 17, 2025

2025   ·   notes   data-structure   ·   data-structure

基于北大《数据结构与算法》第三章内容整理

1. 栈 (Stack)

1.1 基本概念

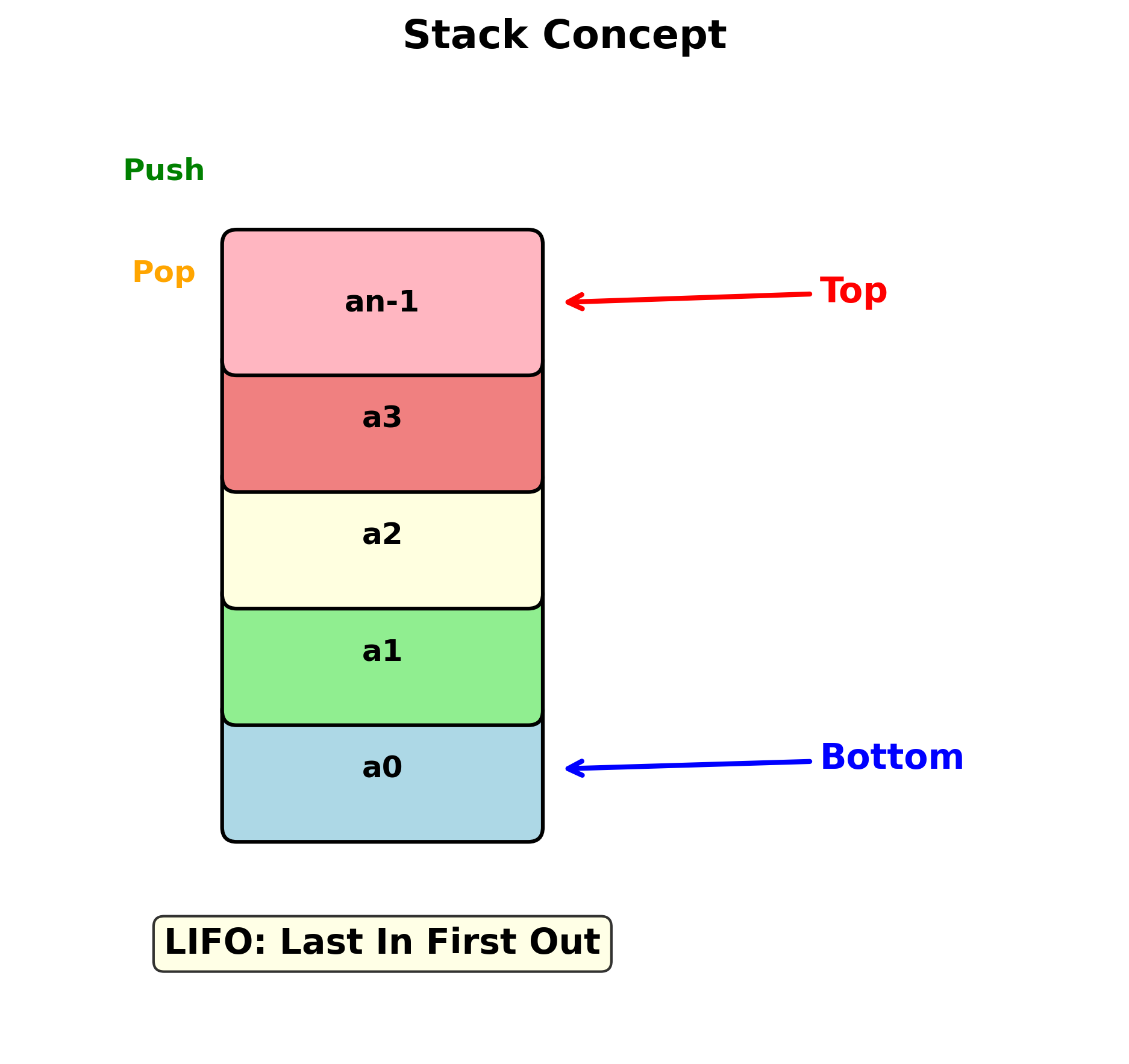
栈是限制在一端访问的线性表，是操作受限的线性结构。

  • 后进先出 (Last-In First-Out，LIFO)，也称”下推表”
  • 栈顶 (top)：允许插入和删除的一端
  • 栈底 (bottom)：不允许操作的一端
  • 压栈 (push)：向栈顶插入元素的操作
  • 出栈 (pop)：从栈顶删除元素的操作

1.2 栈的主要操作

  • 入栈（push）：将元素压入栈顶
  • 出栈（pop）：从栈顶弹出元素
  • 取栈顶元素（top）：获取栈顶元素但不删除
  • 判断栈是否为空（isEmpty）：检查栈是否为空
  • 判断栈是否为满（isFull）：检查栈是否已满

1.3 栈的ADT定义

template <class T>
class Stack {
public:
    void clear();                    // 变为空栈
    bool push(const T item);         // item入栈,成功则返回真,否则返回假
    bool pop(T & item);              // 返回栈顶内容并弹出,成功返回真,否则返回假
    bool top(T& item);               // 返回栈顶内容但不弹出,成功返回真,否则返回假
    bool isEmpty();                  // 若栈已空返回真
    bool isFull();                   // 若栈已满返回真
};

1.4 栈的实现方式

1.4.1 顺序栈（Array-based Stack）

使用向量实现，本质上是顺序表的简化。关键是确定哪一端作为栈顶。

类定义：

template <class T>
class arrStack : public Stack<T> {
private:
    int mSize;      // 栈中最多可存放的元素个数
    int top;        // 栈顶位置，应小于mSize
    T *st;          // 存放栈元素的数组
public:
    arrStack(int size) {
        mSize = size;
        st = new T[mSize];
        top = -1;
    }
    ~arrStack() {
        delete [] st;
    }
    void clear() {
        top = -1;
    }
};

顺序栈的生成方向：

通常使用”向上生成”的栈：

  • 空栈：top == -1
  • 入栈后：top++
  • 出栈后：top--
  • 栈满：top == MAXNUM-1

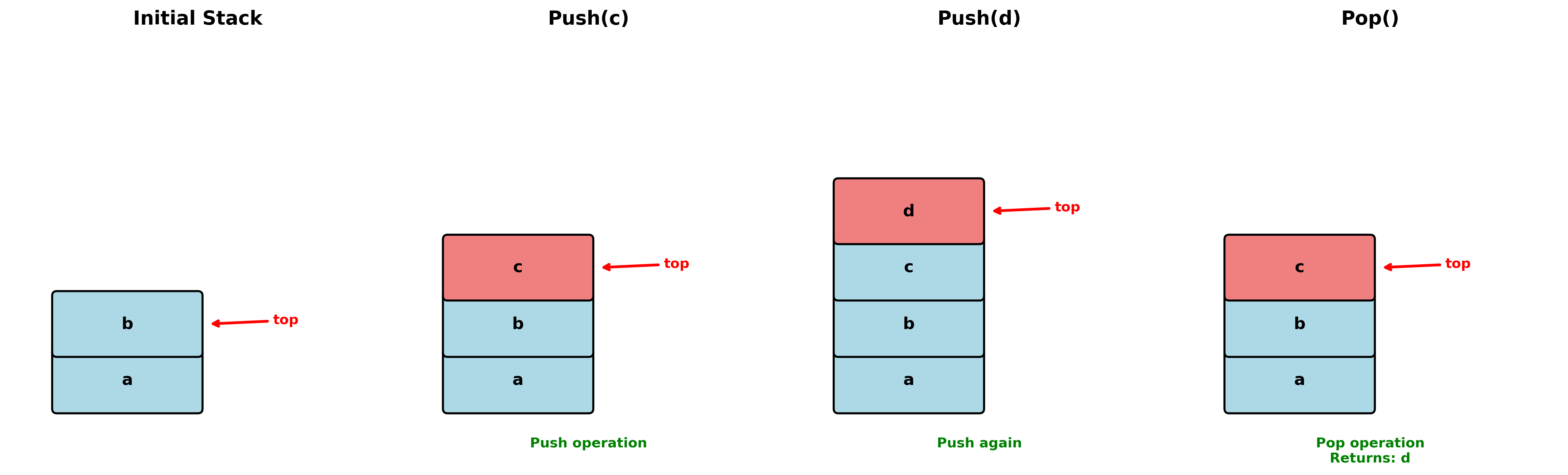
入栈操作：

bool arrStack<T>::push(const T item) {
    if (top == mSize-1) {           // 栈已满
        cout << "栈满溢出" << endl;
        return false;
    }
    else {
        st[++top] = item;           // 新元素入栈并修改栈顶指针
        return true;                // 先执行++，而后执行进栈操作！
    }
}

出栈操作：

bool arrStack<T>::pop(T & item) {
    if (top == -1) {                // 栈为空
        cout << "栈为空，不能执行出栈操作" << endl;
        return false;
    }
    else {
        item = st[top--];           // 返回栈顶元素并修改栈顶指针
        return true;
    }
}

取栈顶元素：

bool arrStack<T>::top(T & item) {
    if (top == -1) {                // 栈空
        cout << "栈为空，不能读取栈顶元素" << endl;
        return false;
    }
    else {
        item = st[top];
        return true;
    }
}

顺序栈的溢出：

  • 上溢（Overflow）：当栈中已经有maxsize个元素时，如果再做进栈操作，所产生的”无空间可用”现象
  • 下溢（Underflow）：空栈进行出栈所产生的”无元素可删”现象

1.4.2 链式栈（Linked Stack）

栈的链式存储结构，是运算受限的链表。

特点：

  • 指针方向：从栈顶向栈底
  • 只能在链表头部进行操作，故没有必要像单链表那样附加头结点
  • 栈顶指针就是链表的头指针（top）
  • 无栈满问题（但存在栈空约束）

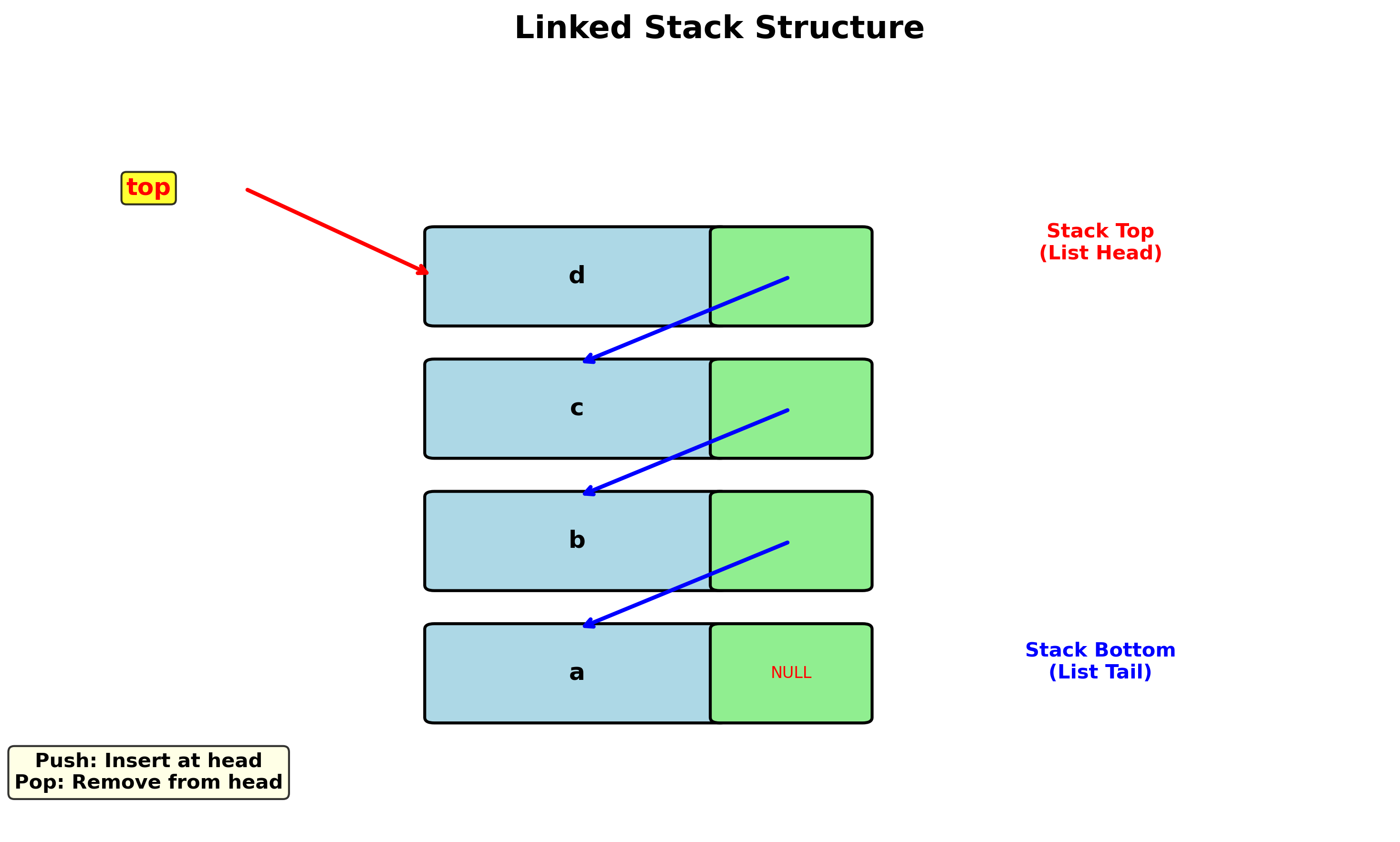
类定义：

template <class T>
class lnkStack : public Stack<T> {
private:
    Link<T>* top;       // 指向栈顶的指针
    int size;           // 存放有效元素的个数
public:
    lnkStack(int defSize) {
        top = NULL;
        size = 0;
    }
    ~lnkStack() {
        clear();
    }
};

压栈操作：

bool lnkStack<T>::push(const T item) {
    // 创建一个新节点，并使其next域赋值top
    Link<T>* tmp = new Link<T>(item, top);
    top = tmp;
    size++;
    return true;
}

出栈操作：

bool lnkStack<T>::pop(T& item) {
    Link<T> *tmp;
    if (size == 0) {
        cout << "栈为空，不能执行出栈操作" << endl;
        return false;
    }
    item = top->data;
    tmp = top->next;
    delete top;
    top = tmp;
    size--;
    return true;
}

1.5 顺序栈和链式栈的比较

时间效率：

  • 所有操作都只需常数时间
  • 顺序栈和链式栈在时间效率上难分伯仲

空间效率：

  • 顺序栈须说明一个固定的长度
  • 链式栈的长度可变，但增加结构性开销

实际应用：

  • 顺序栈比链式栈用得更广泛些

1.6 栈的应用

满足后进先出特性，都可以使用栈，应用广泛。常用来处理具有递归结构的数据应用。

1.6.1 数制转换

十进制N和其它进制数的转换基于原理：

N = (N div d) * d + N mod d

例如 (1348)₁₀ = (2504)₈：

N N div 8 N mod 8
1348 168 4
168 21 0
21 2 5
2 0 2

读取余数序列：2504

1.6.2 括号匹配检验

检查表达式中的括号是否都匹配：

bool isValid(string s) {
    stack<char> st;
    for (char c : s) {
        if (c == '(' || c == '[' || c == '{') {
            st.push(c);
        } else {
            if (st.empty()) return false;
            char top = st.top();
            st.pop();
            if ((c == ')' && top != '(') ||
                (c == ']' && top != '[') ||
                (c == '}' && top != '{')) {
                return false;
            }
        }
    }
    return st.empty();
}

1.6.3 迷宫问题

使用回溯算法求解迷宫路径：

typedef struct NodeMaze {
    int x, y, d;
} DataType;

算法框架：

void mazeFrame() {
    创建一个（保存探索过程的）空栈；
    把入口位置入栈;
    while (栈不空) {
        取栈顶位置并设置为当前位置;
        while (当前位置存在试探可能) {
            取下一个试探位置;
            if (下一个位置是出口) {
                打印栈中保存的探索过程然后返回；
            }
            if (下一个位置是通道) {
                把下一个位置进栈并且设置为的当前位置;
            }
        }
        弹出栈顶元素;  // 实现回溯
    }
}

1.7 栈与递归

1.7.1 递归概念

递归是指在调用一个函数的过程中又直接调用或间接调用了函数自身。

直接调用示例：

long fact(int n) {  // 求阶乘
    if (n == 1)
        return 1;
    return n * fact(n-1);
}

1.7.2 函数调用过程

多个函数嵌套调用时，按照”后调用先返回”的原则进行。

调用前：

  1. 调用函数将实参、返回地址传递给被调用函数
  2. 为被调用函数分配必要的数据区
  3. 将控制转移到被调用函数入口

调用后：

  1. 传送返回信息
  2. 释放被调用函数的数据区
  3. 把控制转移到调用函数中

1.7.3 递归的实现

递归程序必须具有：

  • 有递推公式（1个或多个）
  • 有递归结束条件（1个）

编写递归函数时必须有：

  • 一个（或者多个）递归调用语句
  • 测试结束语句
  • 先测试，后递归调用

1.8 表达式求值

1.8.1 表达式的分类

  • 中缀(infix)表示：<操作数> <操作符> <操作数>，如 A+B
  • 前缀(prefix)表示：<操作符> <操作数> <操作数>，如 +AB
  • 后缀(postfix)表示：<操作数> <操作数> <操作符>，如 AB+

例如：31 * (5 - 22) + 70

  • 前缀：+*31-5 22 70
  • 后缀：31 5 22 - * 70 +

1.8.2 中缀表达式的计算次序

  1. 先执行括号内的计算，后执行括号外的计算
  2. 在无括号或同层括号时，先乘(*)、除(/)，后作加(+)、减(-)
  3. 在同一个层次，若有多个乘除或加减的运算，按自左至右顺序执行

1.8.3 后缀表达式的求值

计算规则：

  • 后缀表达式不含括号
  • 运算符放在两个参与运算的语法成分的后面
  • 所有求值计算皆按运算符出现的顺序，严格从左向右进行

求值算法： 需要一个存放操作数的栈：

  1. 从左往右扫描表达式
  2. 遇到操作数进栈
  3. 遇到运算符时从栈中弹出两个操作数计算，并将计算的结果再压入栈
  4. 扫描结束时，栈顶元素就是最后的结果

1.8.4 中缀到后缀表达式的转换

转换算法： 需要一个存放运算符的栈：

  1. 从左往右扫描表达式，为操作数则输出
  2. 遇到运算符，判断：
    • 为’(‘立刻入栈
    • 为运算符，需等到它的两个操作数输出后、并且后面无运算符或后面的运算符优先级低于该运算符，再输出
    • 为’)’将栈中这对括号之间的操作符依次弹出并输出，最后弹出’(‘

详细步骤：

  • 当输入是操作数，直接输出到后缀表达式序列
  • 当输入的是左括号时，也把它压栈
  • 当输入的是运算符时：
    • While循环：如果栈非空 且 栈顶不是左括号 且 输入运算符的优先级≤栈顶运算符的优先级
      • 将当前栈顶元素弹栈，放到后缀表达式序列中
    • 将输入的运算符压入栈中
  • 当输入的是右括号时：
    • 把栈中的元素依次弹出，直到遇到第一个左括号为止
    • 将弹出的元素输出到后缀表达式的序列中（弹出的开括号不放到序列中）

1.8.5 计算器类的实现

class Calculator {
private:
    Stack<double> s;    // 这个栈用于压入保存操作数
    bool GetTwoOperands(double& opd1, double& opd2);   // 从弹出两个操作数
    void Compute(char op);  // 取两个操作数，并按op对两个操作数进行计算
public:
    Calculator(void){};     // 创建计算器实例，开辟一个空栈
    void Run(void);         // 读入后缀表达式，遇到符号"="时，求值计算结束
    void Clear(void);       // 计算器的清除，为随后的下一次计算做准备
};

2. 队列 (Queue)

2.1 基本概念

队列是只允许在一端删除，在另一端插入的线性表。

  • 先进先出 (FIFO, First In First Out)
  • 队头 (front)：允许删除的一端
  • 队尾 (rear)：允许插入的一端

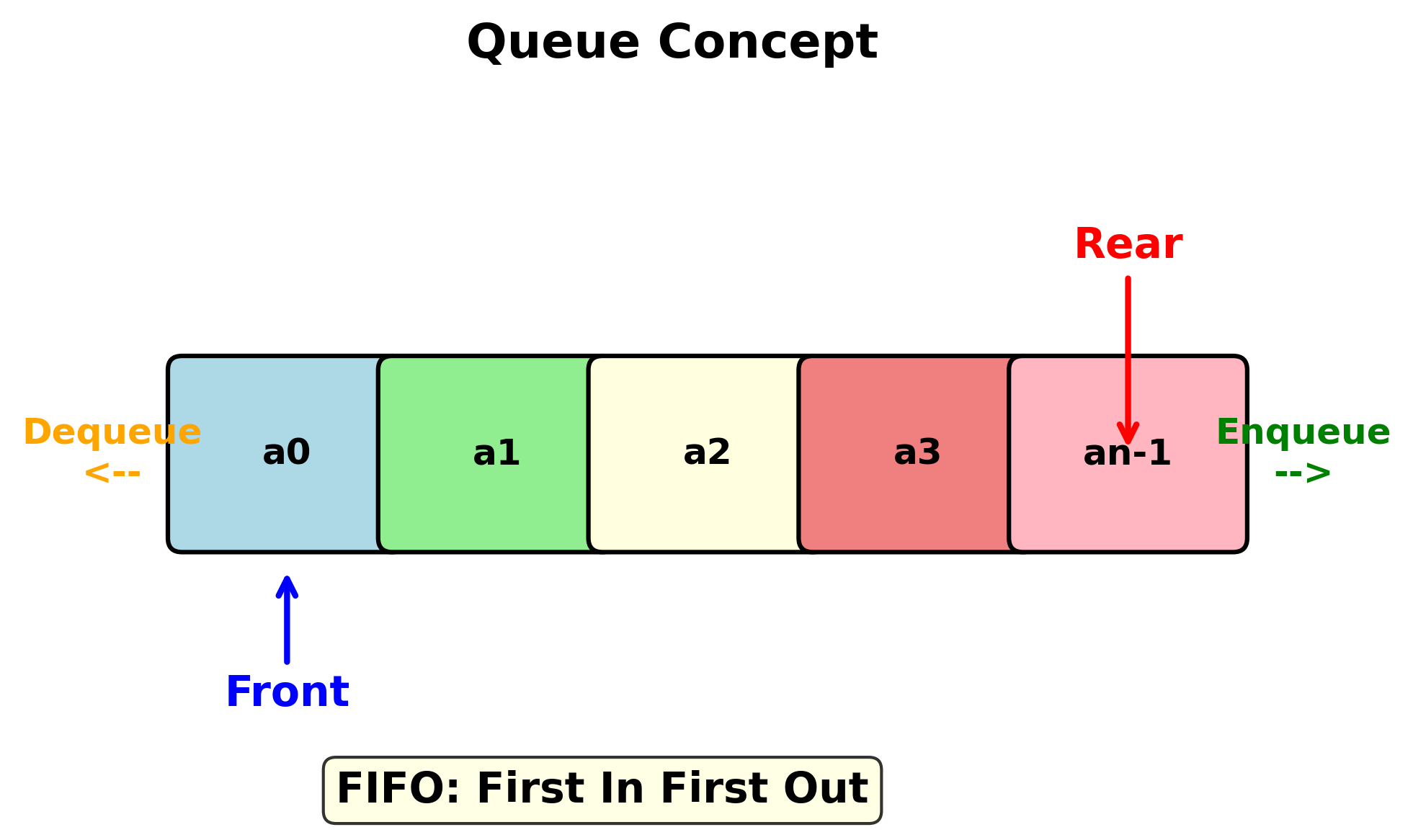
2.2 队列的主要操作

  • 入队列（enQueue）：将元素添加到队尾
  • 出队列（deQueue）：从队头删除元素
  • 取队首元素（getFront）：获取队头元素但不删除
  • 判断队列是否为空（isEmpty）：检查队列是否为空

2.3 队列的ADT定义

template <class T>
class Queue {
public:
    void clear();                    // 变为空队列
    bool enQueue(const T item);      // 将item插入队尾，成功则返回真，否则返回假
    bool deQueue(T& item);           // 返回队头元素并将其从队列中删除，成功则返回真
    bool getFront(T& item);          // 返回队头元素，但不删除，成功则返回真
    bool isEmpty();                  // 返回真，若队列已空
    bool isFull();                   // 返回真，若队列已满
};

2.4 队列的实现方式

2.4.1 顺序队列

用向量存储队列元素，用两个变量分别指向队列的前端(front)和尾端(rear)。

  • front：指向当前待出队的元素位置（地址）
  • rear：指向当前待入队的元素位置（地址）

普通顺序队列的缺陷：

当r == MAXNUM时，再做插入就会产生溢出，而实际上这时队列的前端还有许多空的可用的位置，这种现象称为假溢出。

2.4.2 循环队列

解决方法： 把数组elem[MAXNUM]从逻辑上看成一个环。

判空满条件：

  • 队空条件：front == rear
  • 队满条件：(rear+1) % MAXNUM == front

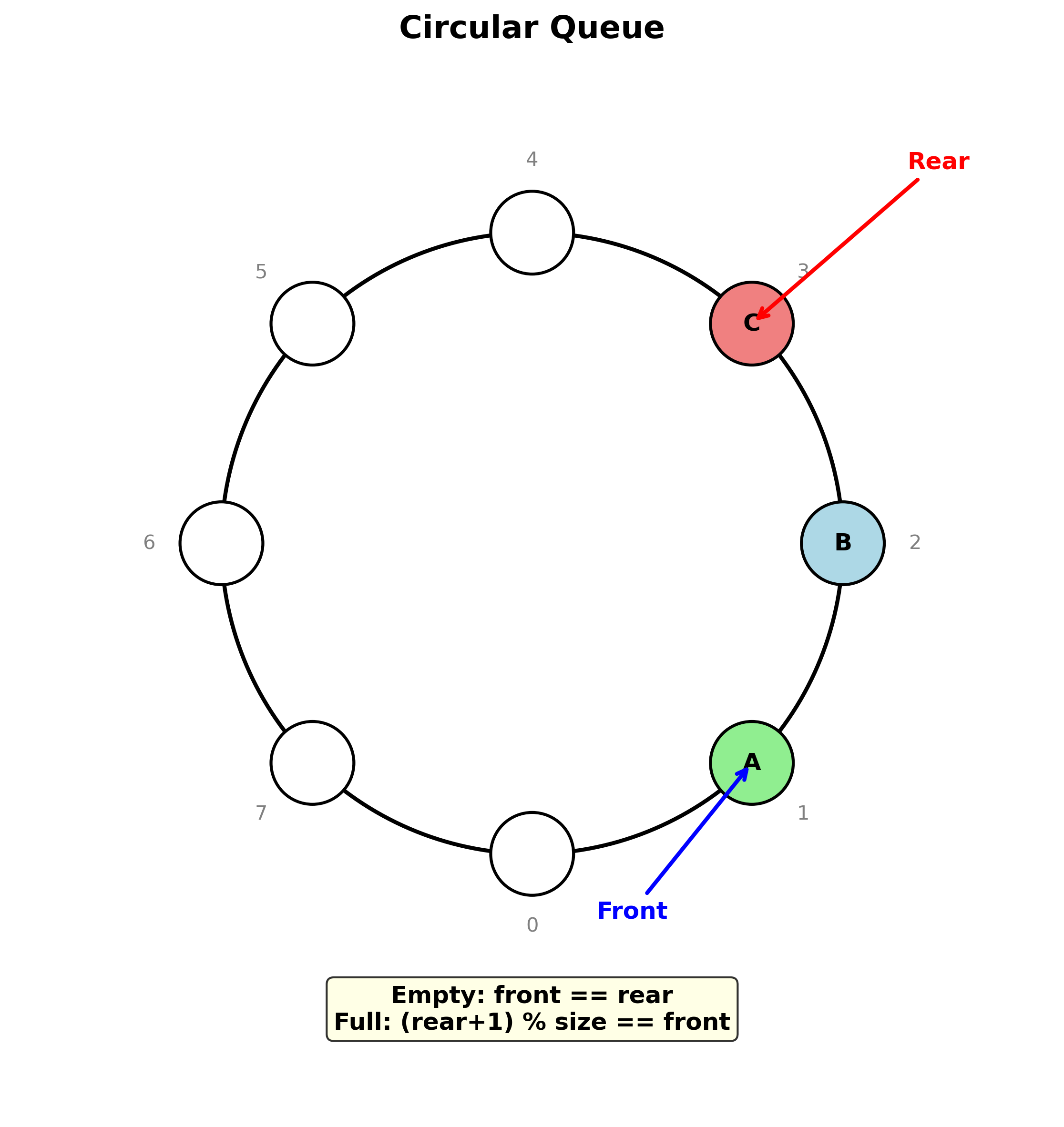
类定义：

class arrQueue: public Queue<T> {
private:
    int mSize;      // 存放队列的数组的大小
    int front;      // 表示队头所在位置的下标
    int rear;       // 表示待入队元素所在位置的下标
    T *qu;          // 存放类型为T的队列元素的数组
public:
    arrQueue(int size) {
        mSize = size + 1;   // 浪费一个存储空间，以区别队列空和队列满
        qu = new T[mSize];
        front = rear = 0;
    }
    ~arrQueue() {
        delete [] qu;
    }
};

入队列操作：

bool arrQueue<T>::enQueue(const T item) {
    if (((rear + 1) % mSize) == front) {
        cout << "队列已满，溢出" << endl;
        return false;
    }
    qu[rear] = item;
    rear = (rear + 1) % mSize;  // 循环后继
    return true;
}

出队列操作：

bool arrQueue<T>::deQueue(T& item) {
    if (front == rear) {
        cout << "队列为空" << endl;
        return false;
    }
    item = qu[front];
    front = (front + 1) % mSize;
    return true;
}

2.4.3 链式队列

单链表队列：链接指针的方向是从队头指向队尾。

特点：

  • 队头在链头，队尾在链尾
  • 链式队列在进队时无队满问题，但有队空问题
  • 队空条件：front == rear == NULL

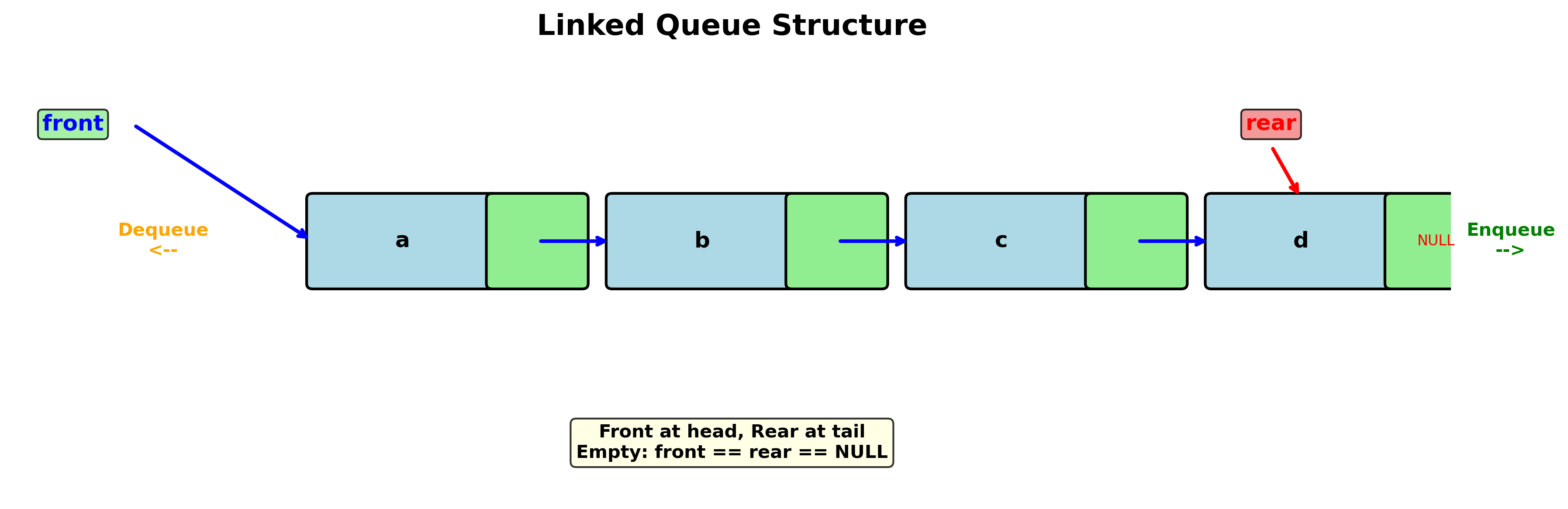
类定义：

template <class T>
class lnkQueue: public Queue<T> {
private:
    int size;           // 队列中当前元素的个数
    Link<T>* front;     // 表示队头的指针
    Link<T>* rear;      // 表示队尾的指针
public:
    lnkQueue(int size) {
        size = 0;
        front = rear = NULL;
    }
    ~lnkQueue() {
        clear();
    }
};

入队操作：

bool lnkQueue<T>::enQueue(const T item) {
    if (rear == NULL) {         // 空队列
        front = rear = new Link<T>(item, NULL);
    } else {                    // 添加新的元素
        rear->next = new Link<T>(item, NULL);
        rear = rear->next;
    }
    size++;
    return true;
}

出队操作：

bool lnkQueue<T>::deQueue(T& item) {
    Link<T> *tmp;
    if (size == 0) {
        cout << "队列为空" << endl;
        return false;
    }
    item = front->data;
    tmp = front;
    front = front->next;
    delete tmp;
    if (front == NULL)
        rear = NULL;
    size--;
    return true;
}

2.5 队列的应用

只要满足先来先服务特性的应用均可采用队列作为其数据组织方式或中间数据结构。

2.5.1 调度或缓冲

  • 消息缓冲器
  • 邮件缓冲器
  • 计算机硬设备之间的通信
  • 操作系统的资源管理

2.5.2 宽度优先搜索

2.5.3 农夫过河问题

问题描述：

  • 只有人能撑船，船上只有两个位置（包括人）
  • 狼羊、羊菜不能在没人时共处

数据抽象：

  • 农夫、狼、白菜和羊，四个目标各用一位（bit）
  • 目标在起始岸位置：0，目标岸：1
  • 如0101表示农夫、白菜在起始岸，而狼、羊在目标岸

广度优先搜索算法：

  • 采用队列做辅助结构，把本步可以到达的所有状态都放在队列中
  • 从队列中顺序取出状态，对其处理
  • 处理过程中再把下一步可以到达的状态放在队列中
  • 由于队列的操作按照先进先出原则，因此只有前一步的所有情况都处理完后才能进入下一步

2.6 变种的栈或队列结构

  • 双端队列：在队首和队尾都可以插入、删除的队列
  • 双栈：两个底部相连的栈，共享一块数据空间
  • 超队列：是一种被限制的双端队列，删除操作只允许在一端进行，插入操作却可以在两端同时进行
  • 超栈：是一种插入受限的双端队列，即插入限制在一端而删除仍允许在两端进行

2.7 思考题：栈和队列的互模拟

2.7.1 如何用两个栈模拟一个队列？

class MyQueue {
private:
    stack<int> inStack;
    stack<int> outStack;

public:
    void push(int x) {
        inStack.push(x);
    }

    int pop() {
        if (outStack.empty()) {
            while (!inStack.empty()) {
                outStack.push(inStack.top());
                inStack.pop();
            }
        }
        int val = outStack.top();
        outStack.pop();
        return val;
    }

    int peek() {
        if (outStack.empty()) {
            while (!inStack.empty()) {
                outStack.push(inStack.top());
                inStack.pop();
            }
        }
        return outStack.top();
    }

    bool empty() {
        return inStack.empty() && outStack.empty();
    }
};

2.7.2 如何用两个队列模拟一个栈？

基本思路：用一个队列存储数据，另一个队列作为辅助，每次取出元素时将前n-1个元素转移到辅助队列，取出第n个元素，然后交换两个队列的角色。

3. 栈与队列的比较

特性 栈 队列
数据存取方式 LIFO（后进先出） FIFO（先进先出）
插入位置 栈顶 队尾
删除位置 栈顶 队头
主要操作 Push、Pop Enqueue、Dequeue
典型应用 函数调用、表达式求值、DFS、递归 BFS、进程调度、缓冲区

4. 时间复杂度分析

栈的时间复杂度

  • Push：O(1)
  • Pop：O(1)
  • Top：O(1)
  • IsEmpty：O(1)

队列的时间复杂度

  • Enqueue：O(1)
  • Dequeue：O(1)
  • Front：O(1)
  • IsEmpty：O(1)

5. 练习题目

  1. 将1，2，3，…，n顺序入栈，其输出序列为p₁, p₂, p₃，…，pₙ，若p₁=n，则pᵢ为__？ 答案：N-i+1

  2. 假设以数组A[m]存放循环队列的元素，其头指针是front，当前队列有k个元素，则队列的尾指针为__**** 答案：(front+k)%m

  3. 设栈S和队列Q的初始状态为空，元素a、b、c、d、e、f依次通过栈S，一个元素出栈后即进入队列Q。若这6个元素出队列的顺序是b、d、c、f、e、a，请写出它们进栈出栈的顺序。 答案：a b (b) c d (d) (c) e f (f) (e) (a)

思考题

  1. 给定一个入栈序列，和一个出栈序列，请你写出一个程序，判定出栈序列是否合法？

  2. 给定一个入栈序列，序列长度为N，请计算有多少种出栈序列？ 答案：卡特兰数 Cₙ = (2n)!/(n!(n+1)!)

此笔记基于北大《数据结构与算法》第三章内容整理，涵盖了栈与队列的基本概念、实现方法、应用场景和相关算法。



Enjoy Reading This Article?

Here are some more articles you might like to read next:

  • notes of ML
  • notes of VCI
  • notes of AIP
  • notes of AI Math Fundamentals
  • notes of ICS