CV - 7: 对极几何 (Epipolar Geometry)

7.1 双视图立体视觉概述

单视图的局限性

从单幅图像恢复3D信息存在固有的深度模糊性（depth ambiguity）问题：

投影过程中深度信息丢失
无法区分不同深度的点投影到相同像素位置

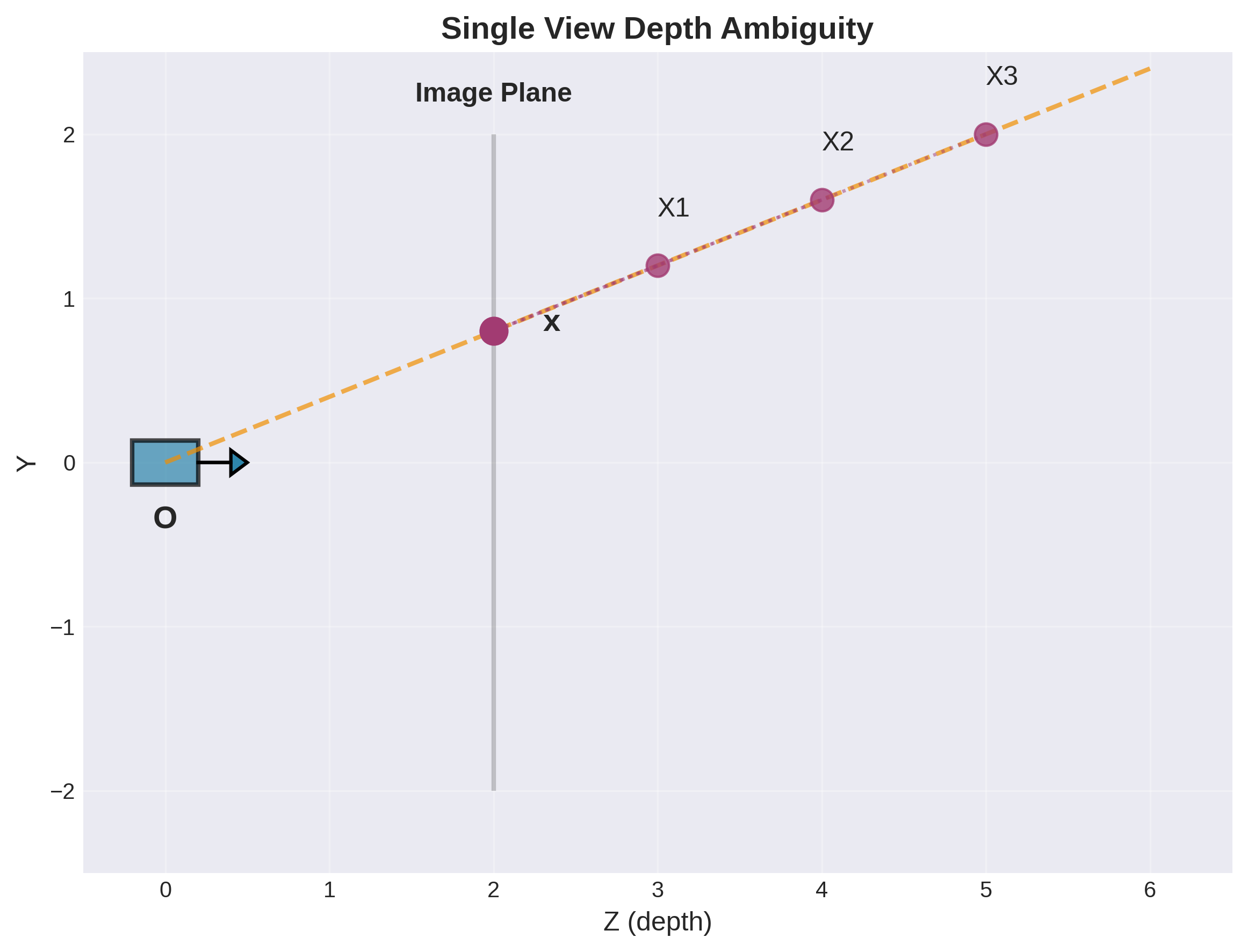
双视图立体视觉

立体视觉（Stereo Vision）通过使用两个标定相机在不同视角下的图像来解决深度模糊性：

利用对应点关系恢复3D结构
模拟人类双眼视觉原理
应用：立体相机、3D重建、自动驾驶等

立体深度相机

Intel RealSense 深度相机是立体视觉的典型应用：

双目红外相机 + RGB相机
主动红外投影辅助
实时深度估计

7.2 典型3D重建流程

多视图3D重建管线

完整的3D重建流程包括：

输入图像（Input Images）
相机标定（Camera Calibration）
特征匹配与对应关系（Correspondences）
深度图估计（Depth Maps）
深度图融合（Depth Map Fusion）
3D重建结果（3D Reconstruction）

双相机配置的优势

使用两个相机可以提供：

相机标定：无需标定板的自标定能力
约束关系：对极约束简化特征匹配
3D估计：通过三角化恢复深度

7.3 对极几何基础

基本配置

考虑两个相机中心 \(O\) 和 \(O'\)：

基线（Baseline）：连接两个相机中心的直线

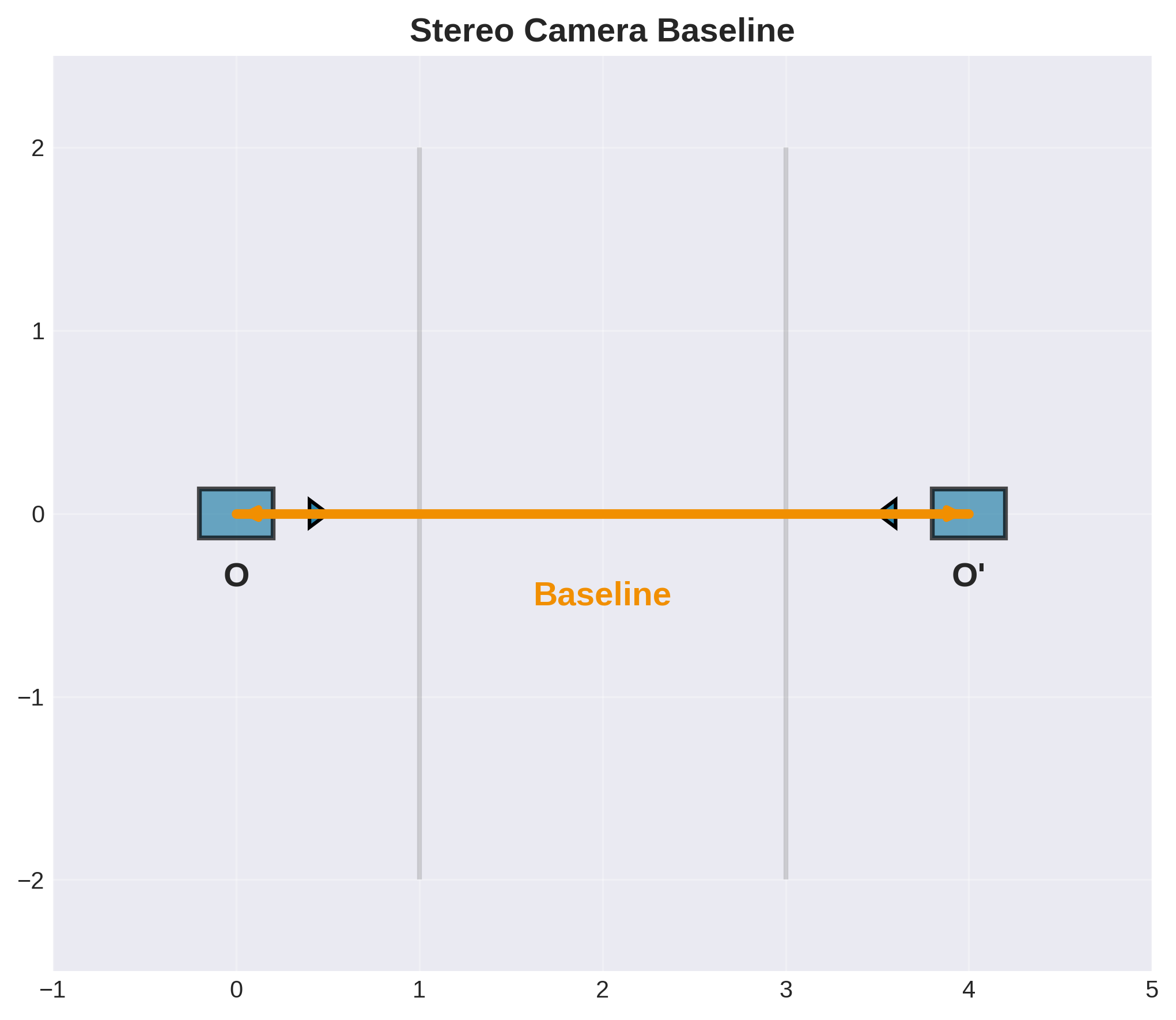
极点（Epipoles）

极点 \(e, e'\) 是基线与两个图像平面的交点：

相当于另一个相机在本相机中的投影
所有对极线都通过极点

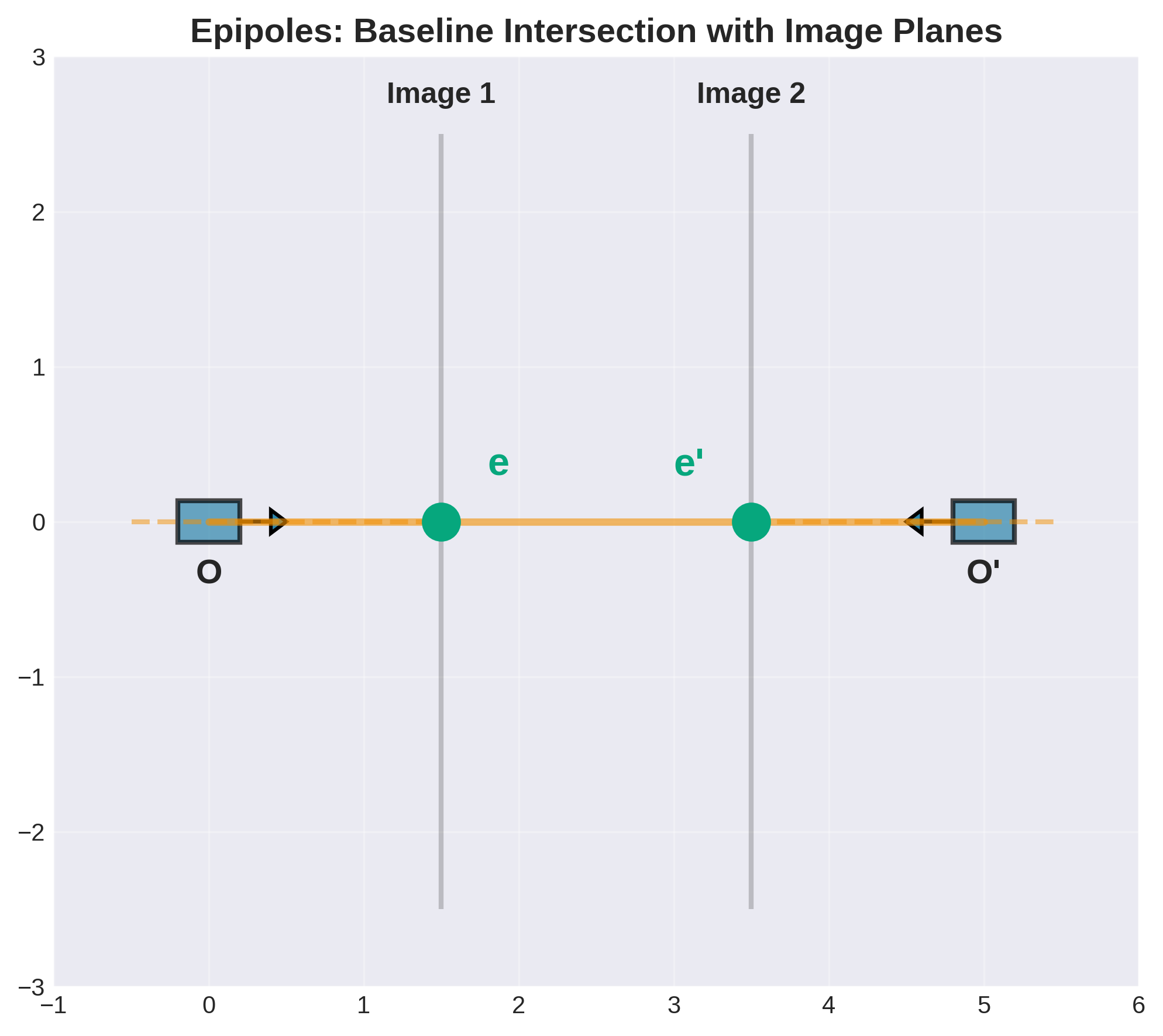
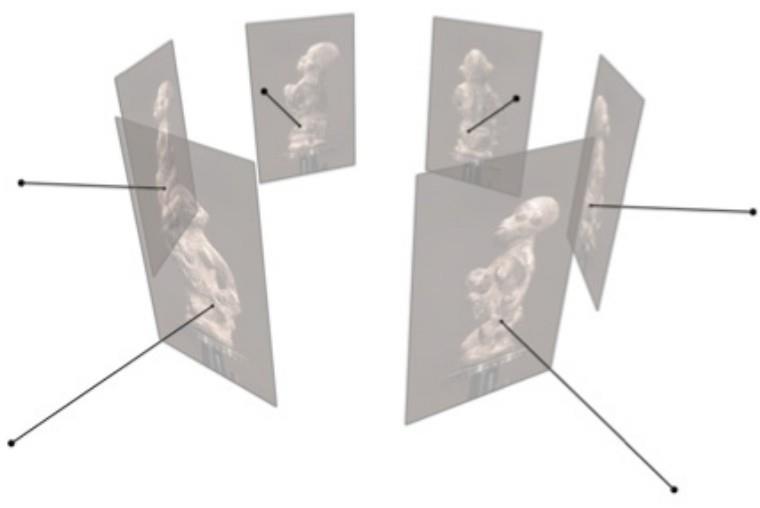
对极平面（Epipolar Plane）

给定3D点 \(X\)，由 \(X, O, O'\) 三点确定的平面称为对极平面：

通过基线的平面族
每个空间点对应一个对极平面

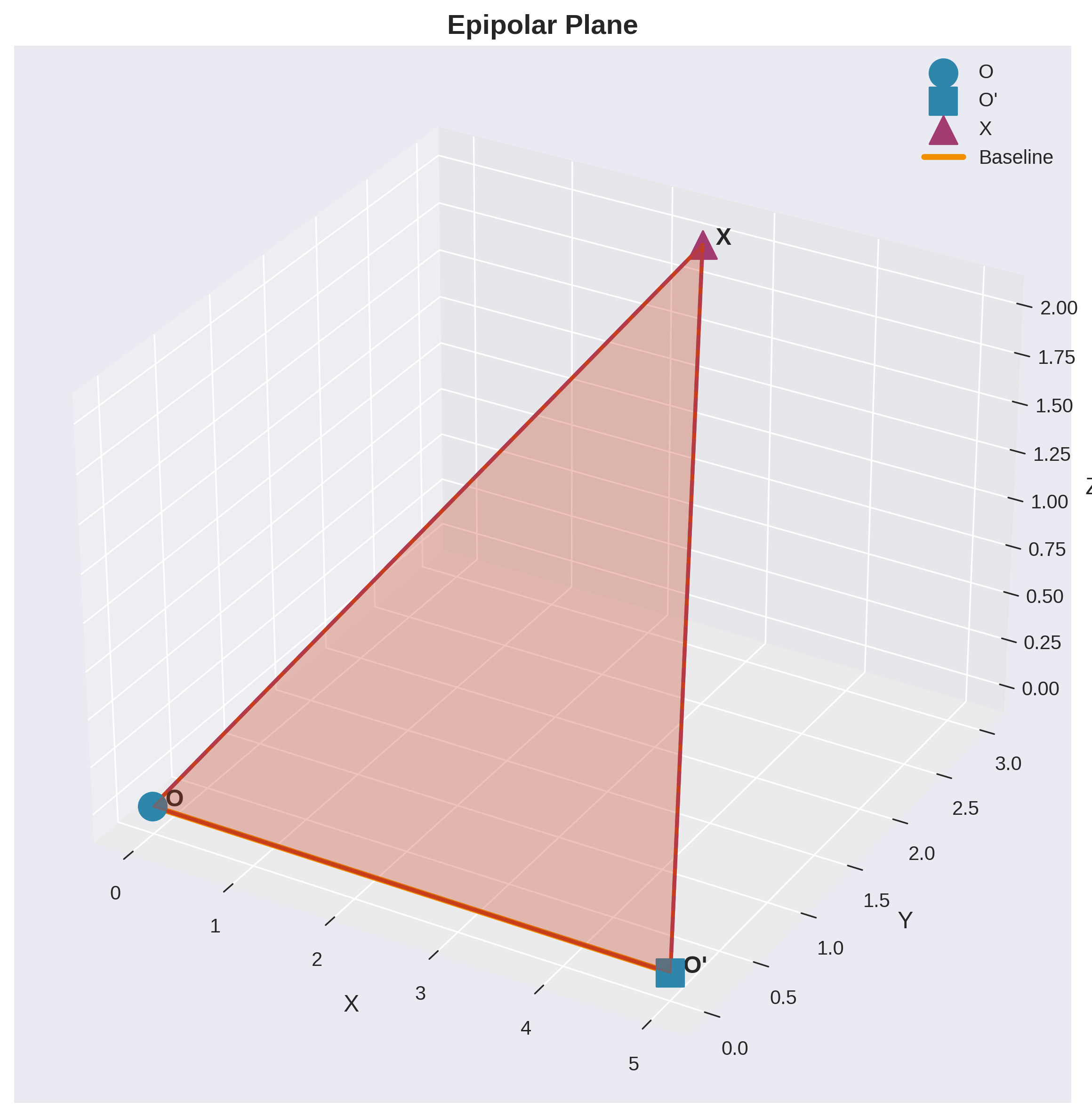
对极线（Epipolar Lines）

对极线是对极平面与图像平面的交线：

连接极点和图像点
成对出现（匹配的对极线）
对应点必在其对极线上

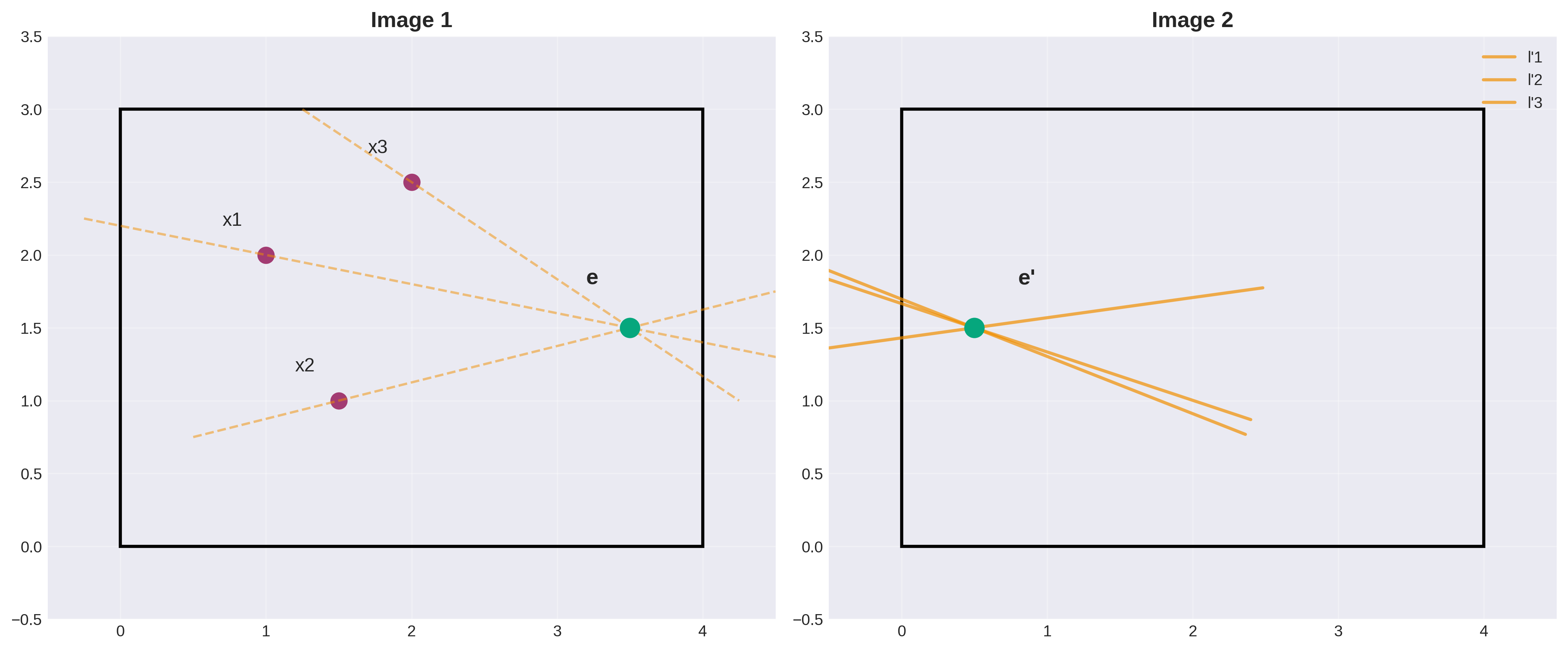
对极几何总结

关键概念：

基线：相机中心连线
极点：基线与图像平面交点
对极线：对极平面与图像平面交线
对极平面：包含 \(X, O, O'\) 的平面

7.4 对极几何的特殊配置

配置1：会聚相机

特点：

相机光轴相交
极点在图像内（可见或不可见）
对极线呈放射状

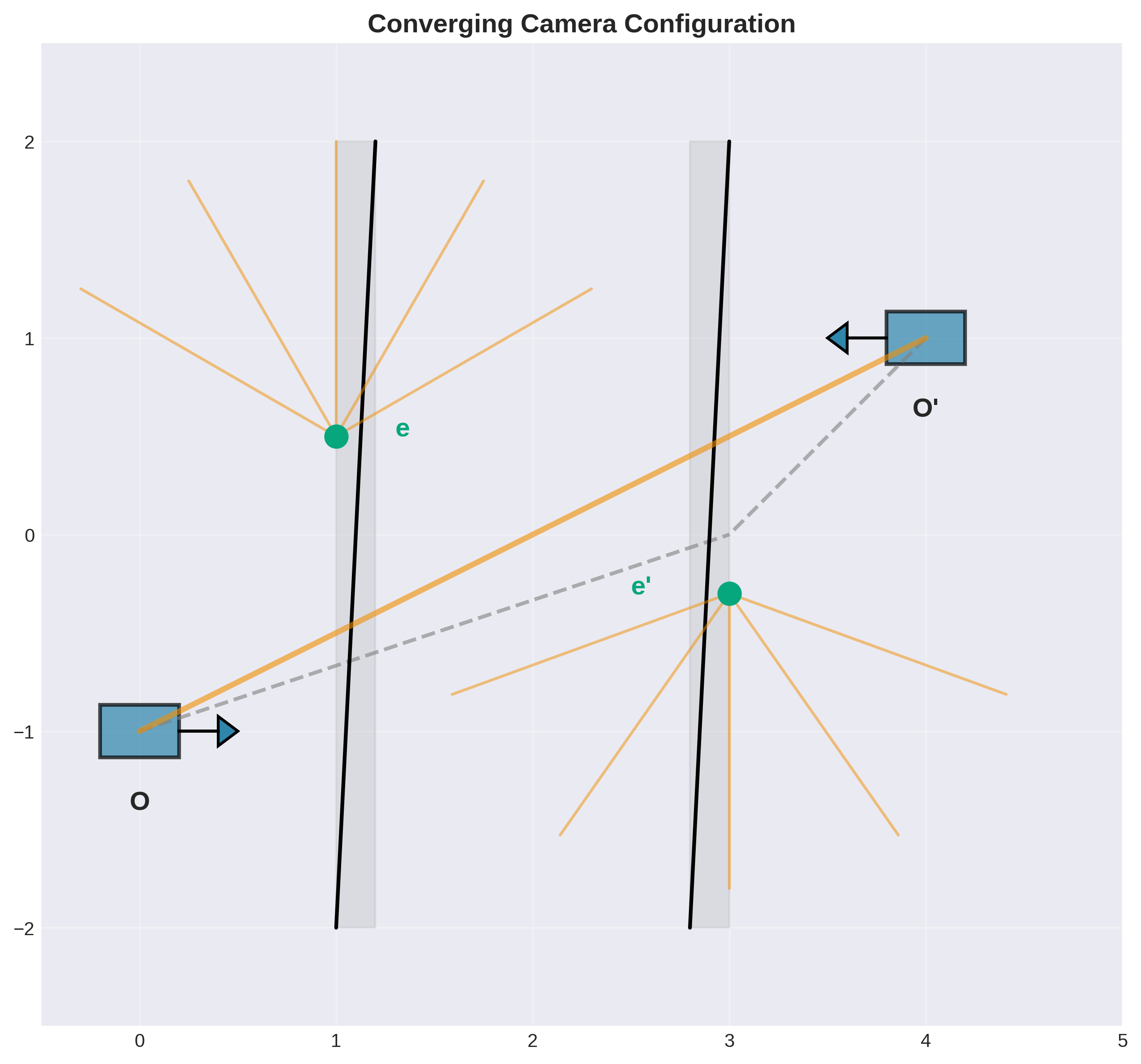
配置2：平行相机

特点：

光轴平行于图像平面
极点在无穷远
对极线平行（同一水平线）

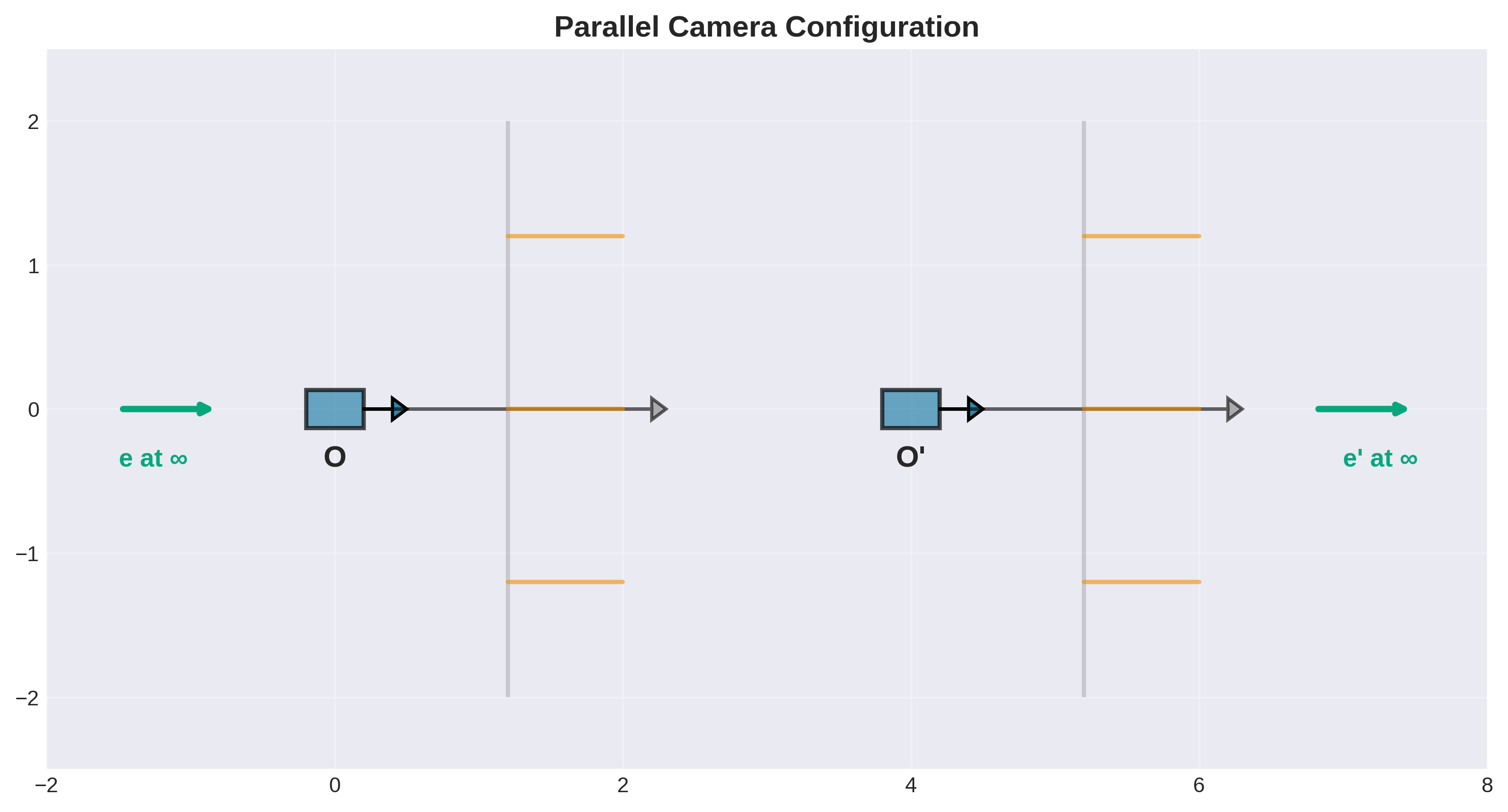
优势：

对应搜索简化为水平线搜索
标准立体视觉配置
易于实现实时处理

配置3：运动垂直于图像平面

特点：

相机沿光轴方向移动
极点与主点重合
对极线呈放射状从中心发出

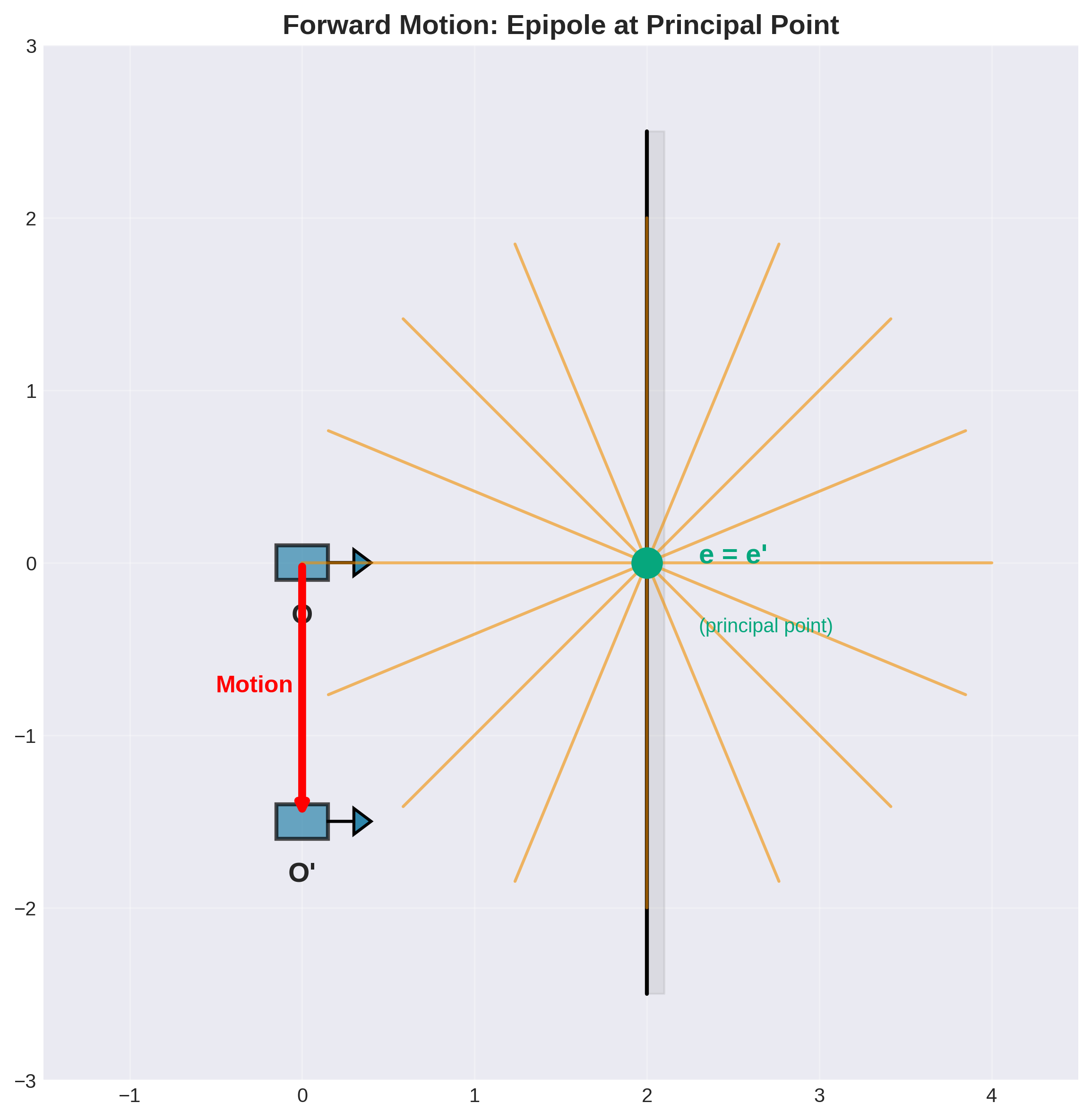
应用：车载相机前向运动

7.5 对极约束（Epipolar Constraint）

对极约束的几何意义

给定图像1中的点 \(x\)，其在图像2中的对应点 \(x'\) 必在对极线上：

\[\text{对极线 } l' = Fx\]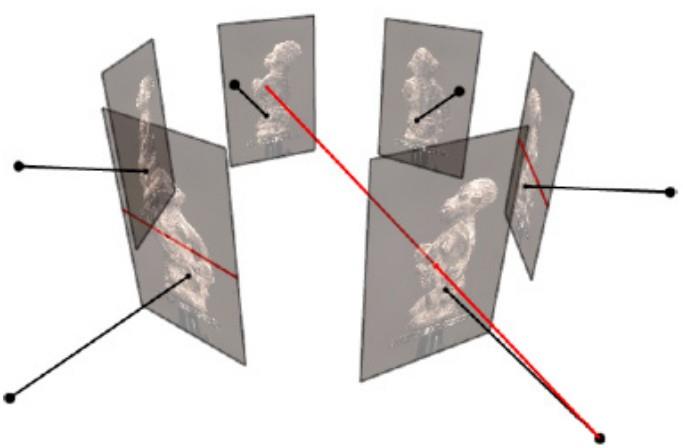

对极约束的重要性

对应搜索：

无约束：在整个图像中搜索（2D）
有对极约束：仅在对极线上搜索（1D）
搜索空间大幅减少

注意：满足对极约束不保证是真正的对应点

7.6 本质矩阵（Essential Matrix）

标定相机的对极约束

假设相机内参已知，世界坐标系设在第一个相机：

投影矩阵：\(K[I \mid 0]\) 和 \(K'[R \mid t]\)
归一化图像坐标：\(\tilde{x} = K^{-1}x_{\text{pixel}}\), \(\tilde{x}' = K'^{-1}x'_{\text{pixel}}\)

本质矩阵的推导

从 \(\tilde{x}' \cong R\tilde{x} + t\) 可知 \(\tilde{x}', R\tilde{x}, t\) 共面。

利用三重积（triple product）：

\[\tilde{x}' \cdot (t \times R\tilde{x}) = 0\]

引入叉积矩阵 \([t]_\times\)：

\[\tilde{x}'^T [t]_\times R \tilde{x} = 0\]

定义本质矩阵：

\[E = [t]_\times R\]

对极约束形式：

\[\tilde{x}'^T E \tilde{x} = 0\]

本质矩阵的性质

自由度：5

平移：3自由度
旋转：3自由度
尺度不变性：-1自由度

秩：2

\([t]_\times\) 秩为2
\(R\) 秩为3
\(E\) 秩为2

SVD分解：\(E = U\Sigma V^T\)，其中 \(\Sigma = \text{diag}(\sigma, \sigma, 0)\)

对极线计算

给定归一化坐标 \(\tilde{x}\) 和 \(\tilde{x}'\)：

对极线 \(l' = E\tilde{x}\)（在图像2中）
对极线 \(l = E^T\tilde{x}'\)（在图像1中）

极点满足：

\(Ee = 0\)（图像1的极点）
\(E^Te' = 0\)（图像2的极点）

7.7 基础矩阵（Fundamental Matrix）

未标定相机的对极约束

当相机内参 \(K, K'\) 未知时，对极约束变为：

\[x'^T F x = 0\]

其中基础矩阵：

\[F = K'^{-T} E K^{-1}\]

基础矩阵的性质

自由度：7

9个元素
det(F) = 0 约束：-1自由度
尺度不变性：-1自由度

秩：2（与本质矩阵相同）

对极线：

\(l' = Fx\)（像素坐标）
\(l = F^Tx'\)（像素坐标）

极点：

\[Fe = 0\]
\[F^Te' = 0\]

7.8 基础矩阵的估计

八点算法（Eight-Point Algorithm）

给定对应点 \((x_i, y_i) \leftrightarrow (x_i', y_i')\)，对极约束为：

\[x'^T F x = (x', y', 1) \begin{bmatrix} f_{11} & f_{12} & f_{13} \\ f_{21} & f_{22} & f_{23} \\ f_{31} & f_{32} & f_{33} \end{bmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = 0\]

展开为线性方程：

\[(x'x, x'y, x', y'x, y'y, y', x, y, 1) \begin{pmatrix} f_{11} \\ f_{12} \\ \vdots \\ f_{33} \end{pmatrix} = 0\]

线性系统

\(n\) 个对应点构成线性系统：

\[\begin{bmatrix} x_1'x_1 & x_1'y_1 & x_1' & y_1'x_1 & y_1'y_1 & y_1' & x_1 & y_1 & 1 \\ \vdots & & & & & & & & \vdots \\ x_n'x_n & x_n'y_n & x_n' & y_n'x_n & y_n'y_n & y_n' & x_n & y_n & 1 \end{bmatrix} \begin{pmatrix} f_{11} \\ \vdots \\ f_{33} \end{pmatrix} = 0\]

即 \(Uf = 0\)

最小点数：8个（因此称为八点算法）

解法：\(f\) 是 \(U^TU\) 最小特征值对应的特征向量

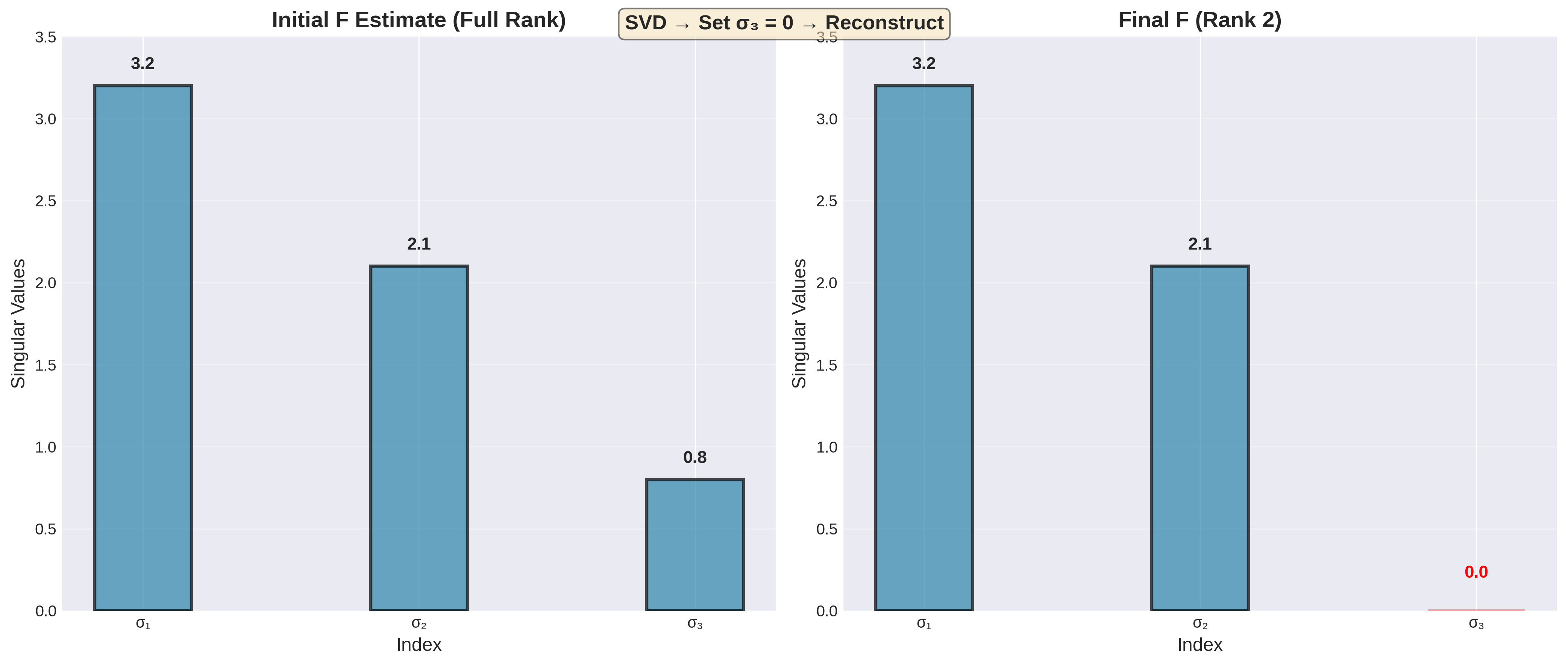
秩-2约束强制

估计的 \(F\) 可能不满足 det(F) = 0，需要强制秩为2：

对 \(F\) 进行SVD：\(F = U\Sigma V^T\)，其中 \(\Sigma = \text{diag}(\sigma_1, \sigma_2, \sigma_3)\)
置最小奇异值为0：\(\Sigma' = \text{diag}(\sigma_1, \sigma_2, 0)\)
重构：\(F_{\text{final}} = U\Sigma' V^T\)

7.9 归一化八点算法

数值不稳定性问题

像素坐标 \((x, y)\) 通常在 \([0, 1000]\) 范围：

\(U\) 矩阵各列数量级差异大：\(10^6, 10^6, 10^3, 10^6, 10^6, 10^3, 10^3, 10^3, 1\)
导致数值不稳定

归一化方案

Hartley算法（TPAMI 1997）：

归一化点坐标：
- 将点集中心移至原点
- 缩放使平均距离为 \(\sqrt{2}\) 像素
估计基础矩阵 \(\tilde{F}\)
强制秩-2约束
反归一化：若归一化变换为 \(T\) 和 \(T'\)，则： \(F = T'^T \tilde{F} T\)

效果：显著提高数值稳定性和估计精度

7.10 非线性优化

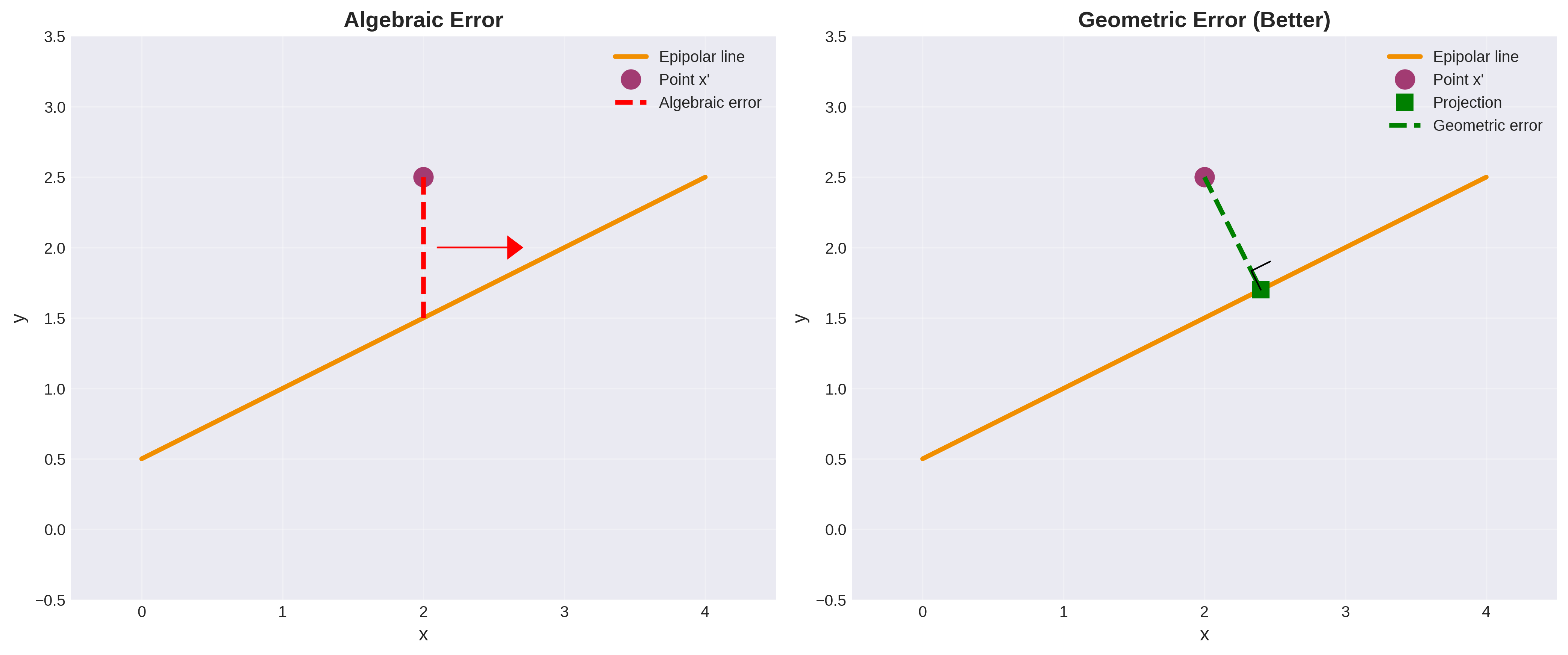
几何误差 vs 代数误差

代数误差（八点算法最小化）：

\[\sum_i (x_i'^T F x_i)^2\]

几何误差（更优）：

\[\sum_i \left[ d(x_i', Fx_i)^2 + d(x_i, F^Tx_i')^2 \right]\]

其中 \(d(\cdot, \cdot)\) 是点到线的距离。

优化方法

使用非线性最小二乘（如Levenberg-Marquardt）最小化几何误差：

初值：归一化八点算法结果
约束：det(F) = 0
参数化：7个自由度

7.11 从本质矩阵恢复相机运动

SVD分解方法

给定 \(E = [t]_\times R = U\Sigma V^T\)：

提取平移： \(t = U(:, 3)\)（最后一列，up to scale）

提取旋转： \(R_1 = UR_{90°}^T V^T\) 或 \(R_2 = UR_{-90°}^T V^T\)

其中 \(R_{90°} = \begin{bmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}\)

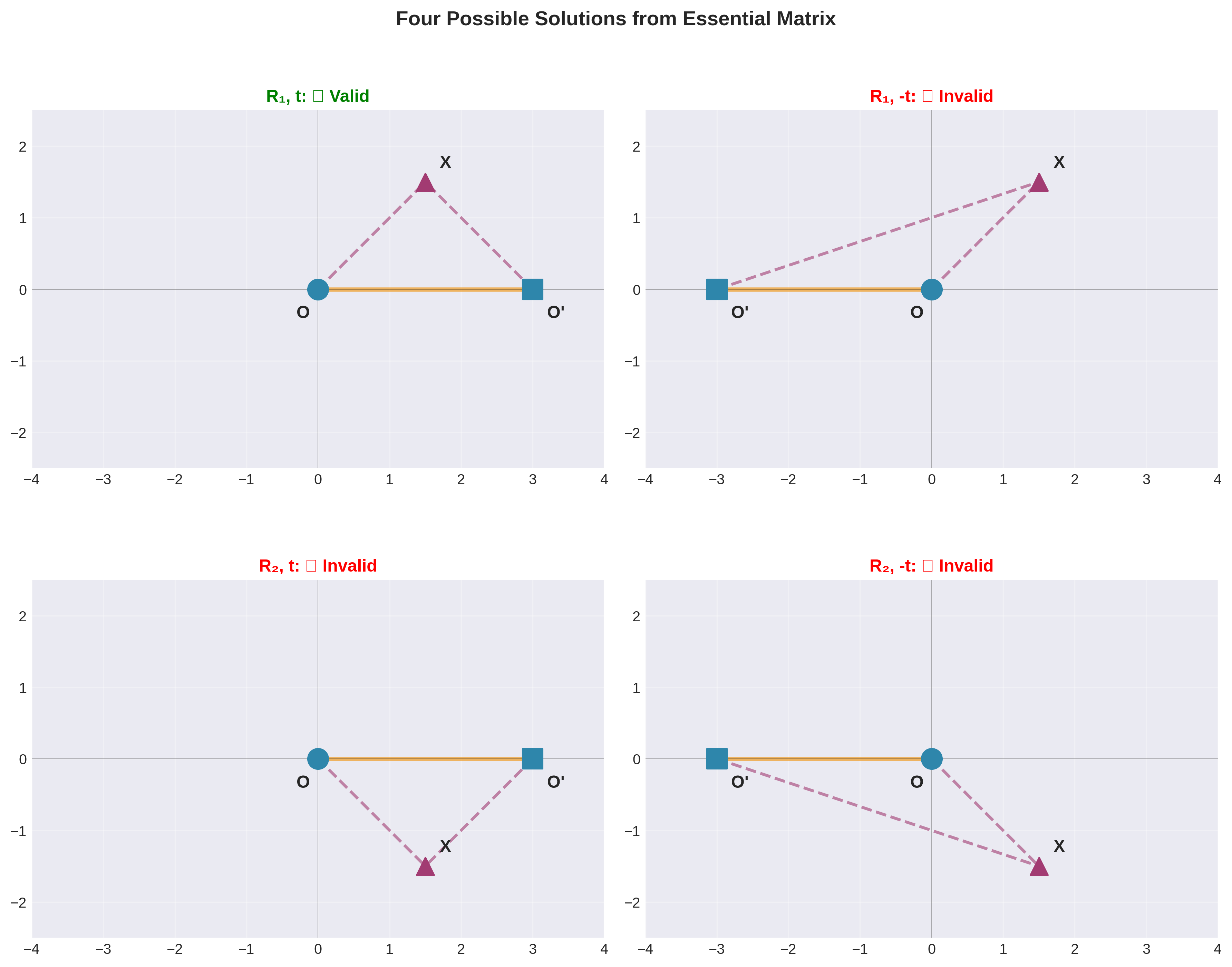
四解歧义

存在4种组合：\((R_1, t), (R_1, -t), (R_2, t), (R_2, -t)\)

消歧方法：深度正定性检查

三角化测试点
选择使点在两个相机前方（正深度）的解

7.12 对极几何的应用

相机自标定

弱标定：估计基础矩阵 \(F\)
强标定：从 \(F\) 和内参估计 \(E\)，进而得到相机外参

立体匹配加速

对应搜索限制在对极线上
从2D搜索降为1D搜索

立体校正

通过图像变换使对极线水平对齐：

运动估计

视觉里程计（Visual Odometry）
SLAM（Simultaneous Localization and Mapping）
五点算法（标定相机情况）

7.13 总结

对极几何核心概念

几何关系：

基线、极点、对极平面、对极线
对极约束：\(x'^T F x = 0\)

数学表示：

本质矩阵 \(E\)：标定相机（5自由度，秩2）
基础矩阵 \(F\)：未标定相机（7自由度，秩2）

估计方法

线性算法：

八点算法（最少8点）
归一化八点算法（提高稳定性）

非线性优化：

最小化几何误差
提高精度

实际应用

3D重建管线
立体视觉系统
相机运动估计
视觉SLAM

参考文献：

Hartley & Zisserman. Multiple View Geometry in Computer Vision, Section 9 & 11
R. Hartley. “In defense of the eight-point algorithm”. TPAMI 1997