CV - 6: 相机标定 (Camera Calibration)

6.1 3D视觉概述

3D视觉的核心目标是从2D图像重建3D结构。这是计算机视觉中的基础问题之一。

核心挑战：单视图歧义性

给定一个相机和一张图像，许多3D点可能投影到同一个2D像素位置。这就是3D视觉的根本难题——单视图歧义性。

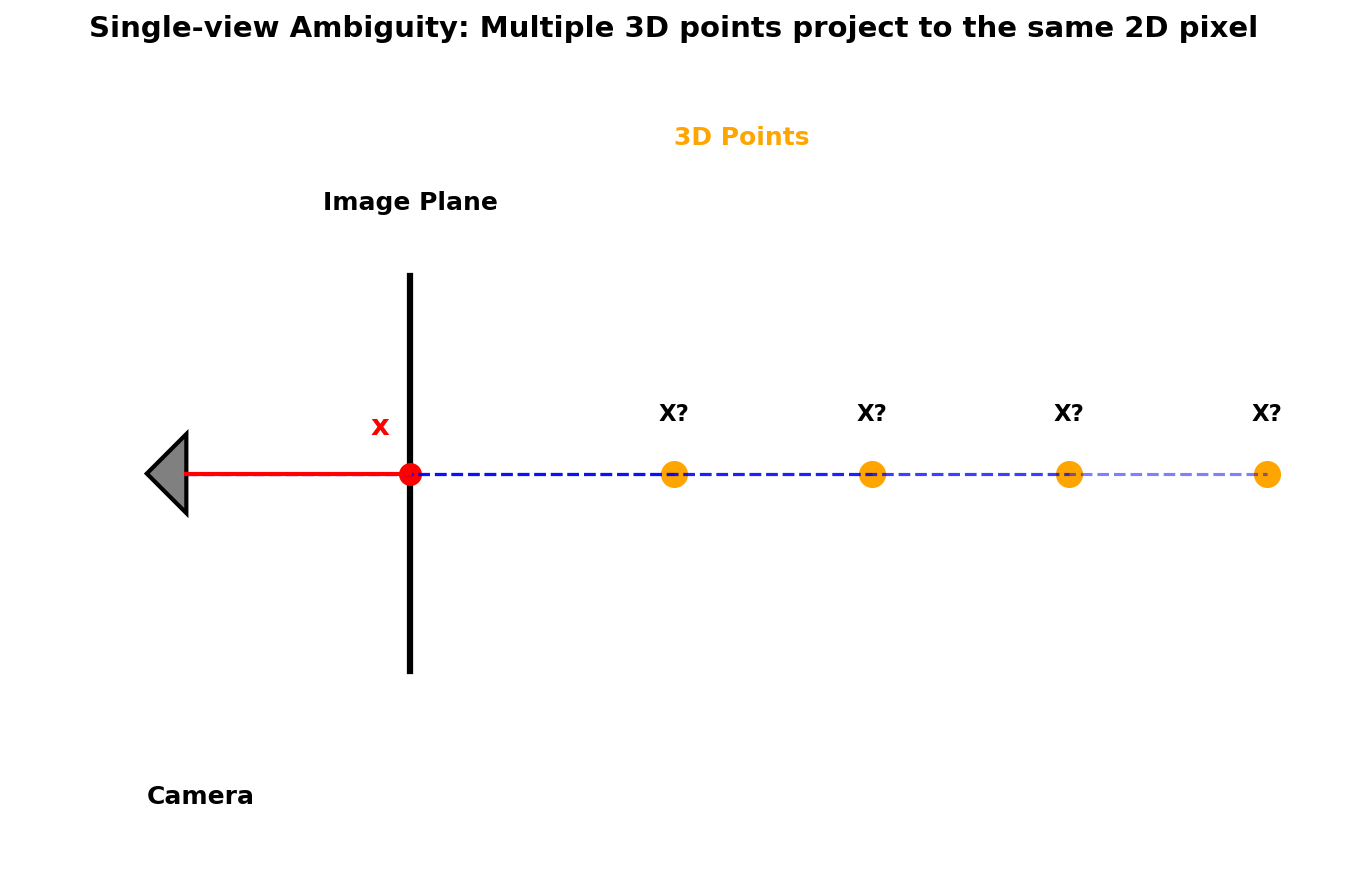
上图展示了单视图歧义性问题：从相机中心发出的一条射线上的所有3D点（标记为X?）都会投影到图像平面上的同一个像素点x。仅凭一个视角，我们无法确定3D点的真实深度位置。

关键问题：如何解决单视图歧义性？

6.2 解决单视图歧义的方法

方法1：主动传感

使用激光、结构光等主动发射光线到场景中，通过测量反射时间或模式畸变直接获取深度信息。

典型设备：

• 激光扫描仪（LiDAR）：通过激光飞行时间测距
• Kinect（结构光）：投射红外结构光模式并分析畸变
• ToF相机：测量光的飞行时间

方法2：立体视觉

使用两个已标定的相机从不同视角观察同一场景，通过三角测量原理从对应点恢复深度。类似于人类的双眼视觉系统。

方法3：多视图几何

移动相机拍摄多张照片，通过寻找不同视角下的对应关系来恢复3D点\(\mathbf{X}\)和相机位置。这是运动恢复结构（Structure from Motion, SfM）的基础。

方法4：形状从明暗 (Shape from Shading)

固定相机位置，在不同光照条件下拍摄多张照片。通过分析表面法线如何影响明暗变化，重建物体的3D几何信息。适用于精细表面细节的恢复。

方法5：数据驱动学习

训练深度神经网络直接从单张图像预测3D信息（如深度图）。网络通过学习大量标注数据，隐式地学习了场景的先验知识和几何规律。

3D视觉任务概览

主要任务包括：

• 相机标定：估计内参矩阵
• 立体视觉：从2张图像估计深度图
• 运动恢复结构：从2+张图像恢复相机和点云
• 形状从明暗：从2+张不同光照图像恢复3D几何

6.3 相机参数回顾

相机投影公式

\[\mathbf{x} \cong \mathbf{K}[\mathbf{R} \mid \mathbf{t}]\mathbf{X}\] \[\begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \cong \begin{bmatrix} f & s & c_x \\ 0 & \alpha f & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} \mathbf{R}_{3\times3} & \mathbf{0}_{3\times1} \\ \mathbf{0}_{1\times3}^T & 1 \end{bmatrix} \begin{bmatrix} \mathbf{I}_{3\times3} & \mathbf{T}_{3\times1} \\ \mathbf{0}_{1\times3}^T & 1 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix}\]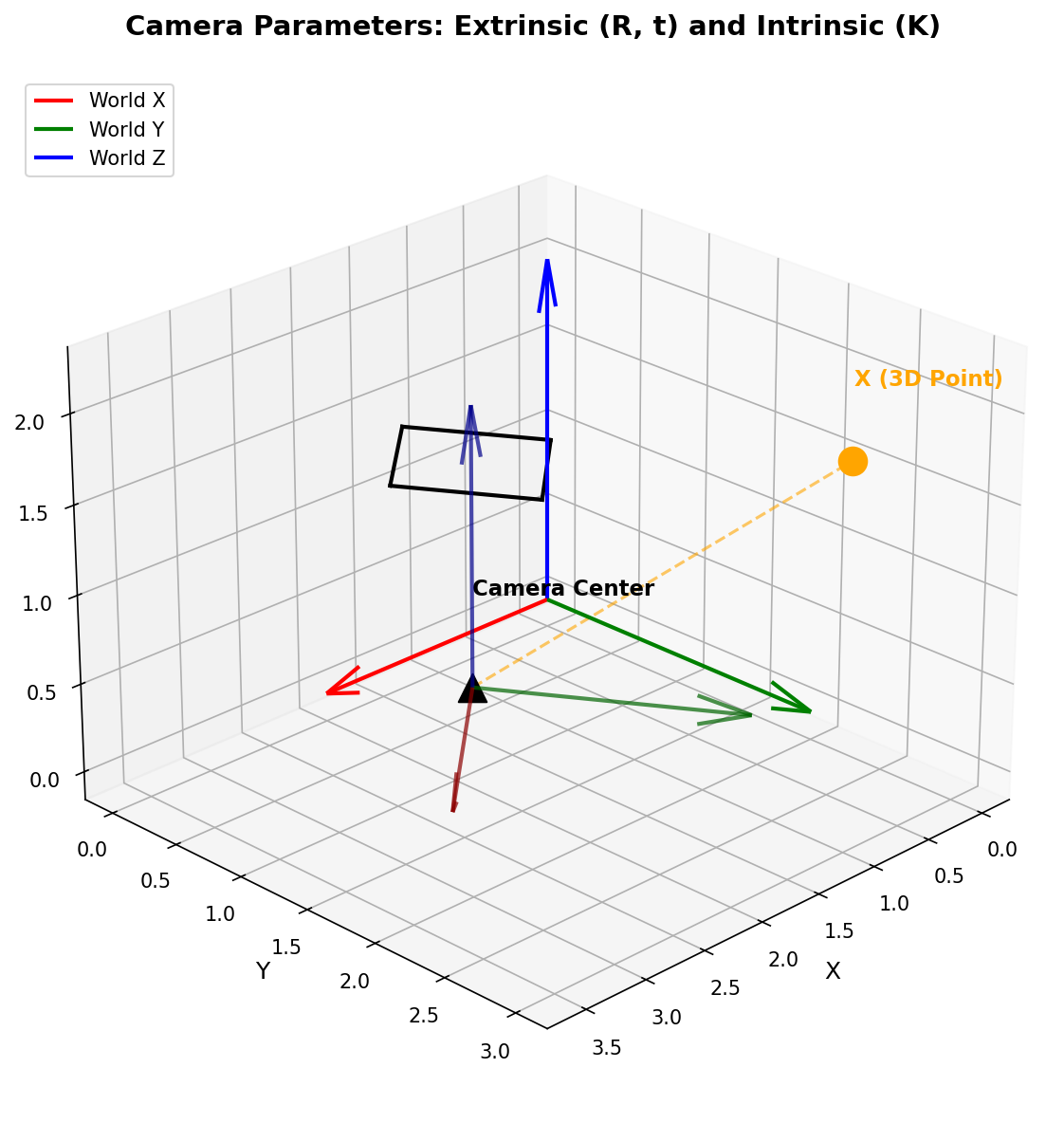

上图展示了相机坐标系统：红色、绿色、蓝色箭头表示世界坐标系的三个轴；相机中心经过旋转\(\mathbf{R}\)和平移\(\mathbf{t}\)变换后建立相机坐标系（深色箭头）；橙色点表示3D空间中的点，通过相机中心投影到图像平面上。

内参矩阵 \(\mathbf{K}\)

\[\mathbf{K} = \begin{bmatrix} f & s & c_x \\ 0 & \alpha f & c_y \\ 0 & 0 & 1 \end{bmatrix}\]

参数说明：

• \(f\)：焦距（focal length）
• \(\alpha\)：纵横比（aspect ratio），等于1除非像素非正方形
• \(s\)：倾斜（skew），等于0除非像素为平行四边形
• \((c_x, c_y)\)：主点（principal point），等于图像中心\((w/2, h/2)\)除非光轴不过图像中心

外参矩阵 \([\mathbf{R} \mid \mathbf{t}]\)

• \(\mathbf{R}\)：旋转矩阵（\(3 \times 3\)），描述世界坐标系到相机坐标系的旋转
• \(\mathbf{t}\)：平移向量（\(3 \times 1\)），描述世界坐标系到相机坐标系的平移

相机矩阵分解

\[\boldsymbol{\Pi} = \begin{bmatrix} p_{11} & p_{12} & p_{13} & p_{14} \\ p_{21} & p_{22} & p_{23} & p_{24} \\ p_{31} & p_{32} & p_{33} & p_{34} \end{bmatrix}\]

可以分解为：

\[\boldsymbol{\Pi} = \mathbf{K}[\mathbf{R} \mid \mathbf{t}]\]

其中：

• \(\mathbf{K}\)是上三角矩阵
• \(\mathbf{R}\)是正交矩阵

可以通过RQ分解恢复\(\mathbf{K}\)和\(\mathbf{R}\)。

6.4 相机标定问题

问题定义

给定\(n\)个已知3D坐标\(\mathbf{X}_i\)和对应的图像投影\(\mathbf{x}_i\)的点，估计相机参数。通常使用标定板（如棋盘格）来提供已知的3D-2D对应关系。

输入：

• 3D世界坐标：\((X_i, Y_i, Z_i)\)
• 对应的2D图像坐标：\((x_i, y_i)\)

输出：

• 相机矩阵\(\boldsymbol{\Pi}\)或分解后的\(\mathbf{K}, \mathbf{R}, \mathbf{t}\)

6.5 相机标定：线性方法

推导过程

投影关系：

\[\mathbf{x}_i \cong \boldsymbol{\Pi}\mathbf{X}_i\] \[\begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \cong \begin{bmatrix} p_{11} & p_{12} & p_{13} & p_{14} \\ p_{21} & p_{22} & p_{23} & p_{24} \\ p_{31} & p_{32} & p_{33} & p_{34} \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix}\]

展开后：

\[x_i = \frac{p_{11}X_i + p_{12}Y_i + p_{13}Z_i + p_{14}}{p_{31}X_i + p_{32}Y_i + p_{33}Z_i + p_{34}}\] \[y_i = \frac{p_{21}X_i + p_{22}Y_i + p_{23}Z_i + p_{24}}{p_{31}X_i + p_{32}Y_i + p_{33}Z_i + p_{34}}\]

叉积形式

利用\(\mathbf{x}_i \times \boldsymbol{\Pi}\mathbf{X}_i = \mathbf{0}\)：

\[\mathbf{x}_i \times \boldsymbol{\Pi}\mathbf{X}_i = \begin{bmatrix} x_i \\ y_i \\ 1 \end{bmatrix} \times \begin{bmatrix} \mathbf{P}_1^T\mathbf{X}_i \\ \mathbf{P}_2^T\mathbf{X}_i \\ \mathbf{P}_3^T\mathbf{X}_i \end{bmatrix} = \mathbf{0}\]

这给出3个方程，但只有2个线性独立（第3个是前两个的线性组合）。

线性方程组

每个点对产生2个方程，对于\(n\)个点：

\[\mathbf{A}_{2n \times 12}\mathbf{p}_{12} = \mathbf{0}_{2n}\]

其中\(\mathbf{p}\)是\(\boldsymbol{\Pi}\)矩阵的12个元素组成的向量。

最小点数

• 未知数：11个自由度（12个元素，尺度不变性减1）
• 方程数：每个点2个方程
• 所需点数：至少6个不共面的点

最小二乘解

实际应用中通常有更多对应点，最小化：

\[E = \|\mathbf{A}\mathbf{p}\|^2 + \lambda(\|\mathbf{p}\|^2 - 1)\]

对\(\mathbf{p}\)求导并令其为0：

\[\mathbf{A}^T\mathbf{A}\mathbf{p} = \lambda\mathbf{p}\]

解：\(\mathbf{p}\)是\(\mathbf{A}^T\mathbf{A}\)最小特征值对应的特征向量。

\(E = \lambda\)（最小特征值）

6.6 RQ分解

QR分解回顾

QR分解是对矩阵\(\mathbf{A}\)的列进行Gram-Schmidt正交化，从第一列开始：

\[\mathbf{A} = \begin{bmatrix} \mathbf{a}_1 & \mathbf{a}_2 & \cdots & \mathbf{a}_n \end{bmatrix} = \begin{bmatrix} \mathbf{e}_1 & \mathbf{e}_2 & \cdots & \mathbf{e}_n \end{bmatrix} \begin{bmatrix} \mathbf{a}_1 \cdot \mathbf{e}_1 & \mathbf{a}_2 \cdot \mathbf{e}_1 & \cdots & \mathbf{a}_n \cdot \mathbf{e}_1 \\ 0 & \mathbf{a}_2 \cdot \mathbf{e}_2 & \cdots & \mathbf{a}_n \cdot \mathbf{e}_2 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \mathbf{a}_n \cdot \mathbf{e}_n \end{bmatrix} = \mathbf{Q}\mathbf{R}\]

RQ分解

RQ分解是对矩阵\(\mathbf{A}\)的行进行Gram-Schmidt正交化，从最后一行开始。

对于估计的相机矩阵\(\boldsymbol{\Pi} = \mathbf{K}[\mathbf{R} \mid \mathbf{t}]\)（\(3 \times 4\)）：

1. 对左侧\(3 \times 3\)子矩阵\(\mathbf{M}\)进行RQ分解得到\(\mathbf{K}\)和\(\mathbf{R}\)
2. 计算平移向量\(\mathbf{t} = \mathbf{K}^{-1}\mathbf{p}_4\)

6.7 相机标定：线性vs非线性

线性方法

优点：

• 易于公式化和求解
• 计算效率高
• 适合初始化

缺点：

• 不直接给出相机参数（需要RQ分解）
• 不能加入约束（如径向畸变）
• 最小化代数误差而非几何误差

非线性方法

在实际应用中，非线性方法更受青睐。

目标函数（几何误差）：

\[\min_{\mathbf{K},\mathbf{R},\mathbf{t}} \sum_{i=1}^n \|\text{proj}(\mathbf{K}[\mathbf{R}\mid\mathbf{t}]\mathbf{X}_i) - \mathbf{x}_i\|_2^2\]

其中\(\text{proj}\)表示透视除法：\(\text{proj}\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} x/z \\ y/z \end{bmatrix}\)

优化方法：

• 使用非线性优化包（如Levenberg-Marquardt）
• 用线性方法的结果初始化
• 可以加入畸变参数、正交性约束等

6.8 三角测量 (Triangulation)

问题定义

给定一个3D点在两个或多个图像中的投影（已知相机矩阵），求该点的3D坐标。这是相机标定的逆问题。

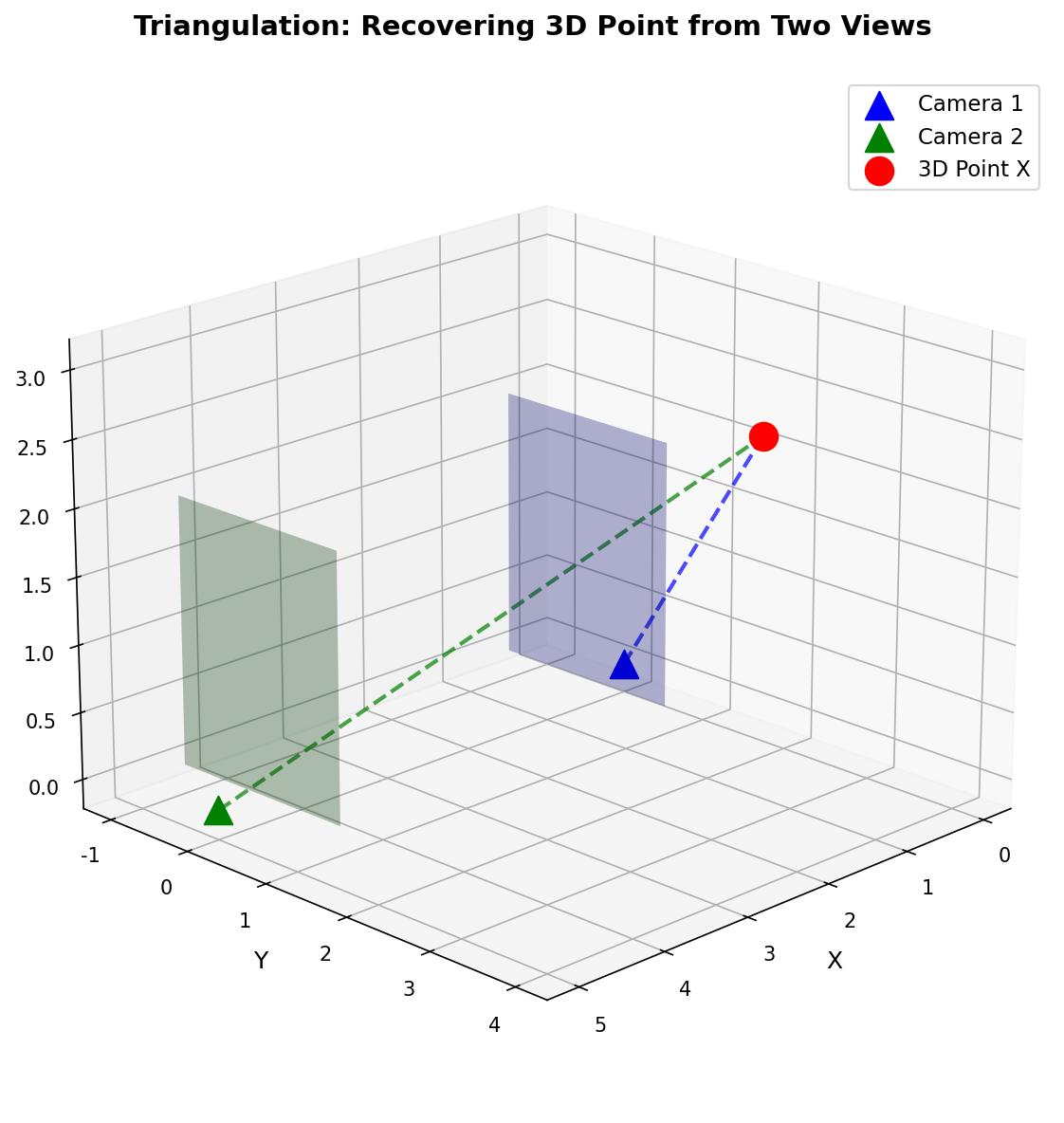
上图展示了三角测量的几何原理：两个不同位置的相机（蓝色和绿色三角形）观察同一个3D点（红色球），该点在两个图像平面（半透明平面）上产生投影。通过已知的相机位置和投影点，可以计算两条视线的交点，从而恢复3D点的位置。

输入：

• 已知相机矩阵\(\boldsymbol{\Pi}_1, \boldsymbol{\Pi}_2\)
• 对应的图像点\(\mathbf{x}_1, \mathbf{x}_2\)

输出：

• 3D点\(\mathbf{X}\)

理想vs实际情况

理想情况：两条视线应该精确相交于3D点\(\mathbf{X}\)。

实际情况：由于噪声和数值误差，两条视线通常不会精确相交，而是相互错开。因此需要寻找最优的3D点位置，使其到两条视线的距离最小（几何方法）或重投影误差最小（优化方法）。

6.9 三角测量方法

方法1：几何方法

找到连接两条视线的最短线段（即两条异面直线的公垂线），取其中点作为\(\mathbf{X}\)的估计。这是一个直观的几何解法，计算简单。

方法2：非线性优化

最小化重投影误差：

\[\min_{\mathbf{X}} \|\text{proj}(\boldsymbol{\Pi}_1\mathbf{X}) - \mathbf{x}_1\|_2^2 + \|\text{proj}(\boldsymbol{\Pi}_2\mathbf{X}) - \mathbf{x}_2\|_2^2\]

这种方法寻找最优的3D点\(\mathbf{X}\)，使得其投影回两个图像平面后，与观测到的像素点之间的欧氏距离平方和最小。这是几何误差的直接优化，通常能得到更准确的结果。

方法3：线性优化

利用叉积形式：

\[\mathbf{x}_1 \cong \boldsymbol{\Pi}_1\mathbf{X} \Rightarrow \mathbf{x}_1 \times \boldsymbol{\Pi}_1\mathbf{X} = \mathbf{0}\] \[\mathbf{x}_2 \cong \boldsymbol{\Pi}_2\mathbf{X} \Rightarrow \mathbf{x}_2 \times \boldsymbol{\Pi}_2\mathbf{X} = \mathbf{0}\]

使用叉积矩阵形式：

\[\mathbf{a} \times \mathbf{b} = [\mathbf{a}]_\times\mathbf{b} = \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix}\begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix}\]

得到：

\[\begin{bmatrix} [\mathbf{x}_1]_\times\boldsymbol{\Pi}_1 \\ [\mathbf{x}_2]_\times\boldsymbol{\Pi}_2 \end{bmatrix}\mathbf{X} = \mathbf{0}\]

每个相机提供2个方程（第3个是前两个的线性组合），对于3个未知数，用约束最小二乘求解：

\[\min_{\mathbf{X}} \|\mathbf{A}\mathbf{X}\|^2 \text{ subject to } \|\mathbf{X}\|^2 = 1\]

解：\(\mathbf{X}\)是\(\mathbf{A}^T\mathbf{A}\)最小特征值对应的特征向量。

齐次坐标的优势

使用齐次坐标\(\mathbf{X} = (X, Y, Z, W)\)，约束\(\|\mathbf{X}\|^2 = 1\)，避免平凡解\(\mathbf{X} = \mathbf{0}\)。

投影公式：

\[x_j = \frac{p_{11}^{(j)}X + p_{12}^{(j)}Y + p_{13}^{(j)}Z + p_{14}^{(j)}W}{p_{31}^{(j)}X + p_{32}^{(j)}Y + p_{33}^{(j)}Z + p_{34}^{(j)}W}\] \[y_j = \frac{p_{21}^{(j)}X + p_{22}^{(j)}Y + p_{23}^{(j)}Z + p_{24}^{(j)}W}{p_{31}^{(j)}X + p_{32}^{(j)}Y + p_{33}^{(j)}Z + p_{34}^{(j)}W}\]

6.10 消失点标定

消失点回顾

消失点是平行线在透视投影中的交点，代表了无穷远处的方向。

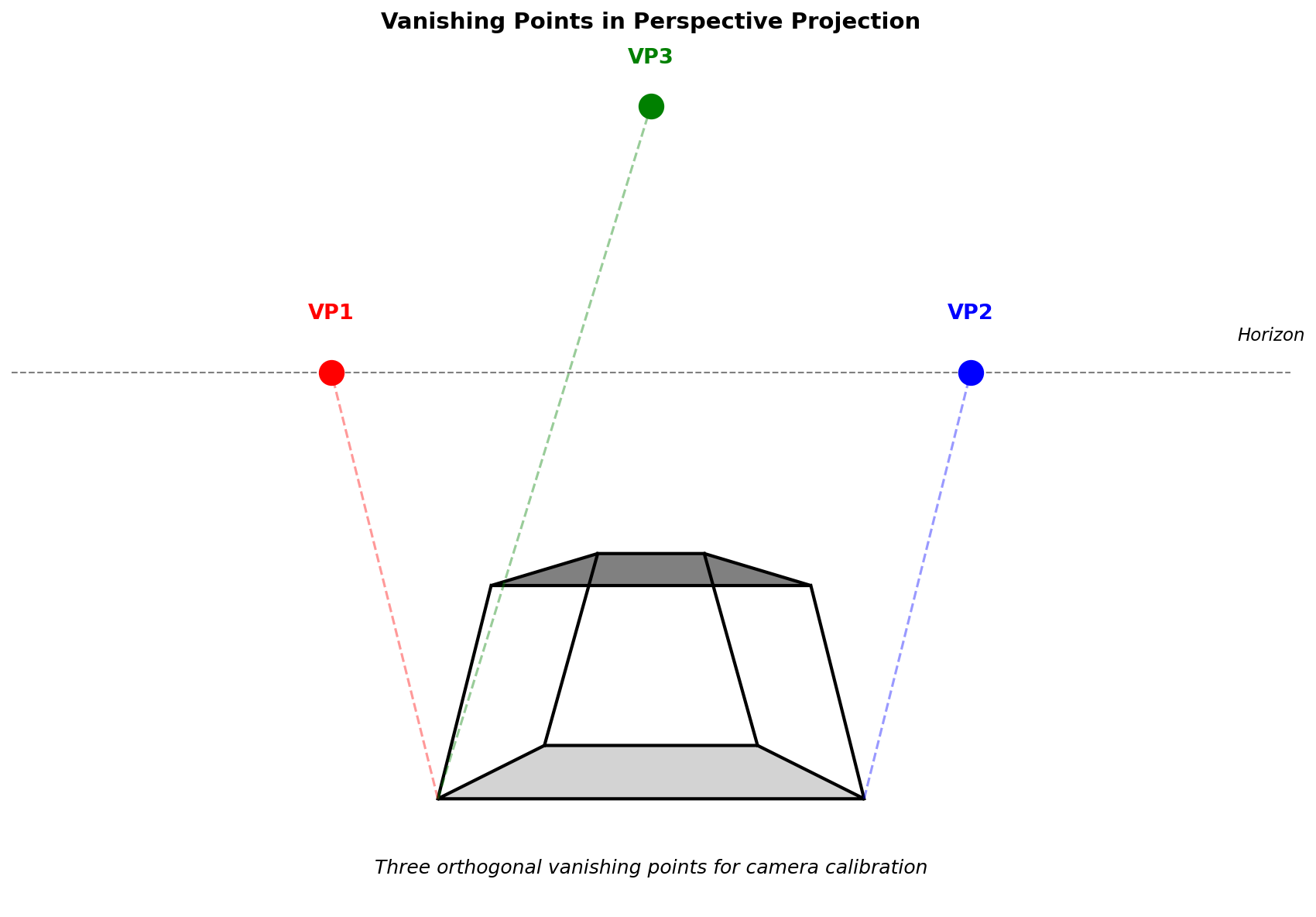
上图展示了消失点的几何意义：建筑物的水平边缘线（红色和蓝色线）延伸后会聚于两个消失点VP1和VP2，垂直边缘线（绿色线）延伸后会聚于垂直消失点VP3。三个消失点对应于场景中三个正交的主方向，这些方向信息可以用来标定相机的内参。

一条直线可以参数化为：

\[\mathbf{X}_t = \begin{bmatrix} X_0 + tD_1 \\ Y_0 + tD_2 \\ Z_0 + tD_3 \\ 1 \end{bmatrix} \cong \begin{bmatrix} X_0/t + D_1 \\ Y_0/t + D_2 \\ Z_0/t + D_3 \\ 1/t \end{bmatrix} \rightarrow \mathbf{X}_\infty = \begin{bmatrix} D_1 \\ D_2 \\ D_3 \\ 0 \end{bmatrix}\]

当\(t \to \infty\)时，点趋向于无穷远点\(\mathbf{X}_\infty\)，其投影为消失点：

\[\mathbf{v} \cong \boldsymbol{\Pi}\mathbf{X}_\infty\]

使用消失点标定

如果世界坐标系没有已知的3D点坐标，在某些特殊场景下，可以使用消失点进行标定。这种方法特别适用于建筑物、室内环境等具有明显正交结构的场景。

适用场景：场景中存在三组正交的消失方向（如建筑物的长、宽、高三个方向）。

正交约束

将世界坐标系与三个正交消失方向对齐：

\[\mathbf{e}_1 = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \quad \mathbf{e}_2 = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}, \quad \mathbf{e}_3 = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\]

消失点\(\mathbf{v}_i\)对应于方向\(\mathbf{e}_i\)：

\[\mathbf{v}_i \cong \boldsymbol{\Pi}\begin{bmatrix} \mathbf{e}_i \\ 0 \end{bmatrix} = \mathbf{K}[\mathbf{R}\mid\mathbf{t}]\begin{bmatrix} \mathbf{e}_i \\ 0 \end{bmatrix} = \mathbf{K}\mathbf{R}\mathbf{e}_i\]

因为\(\mathbf{e}_i^T\mathbf{e}_j = 0\)（正交），所以：

\[\mathbf{e}_i \cong \mathbf{R}^T\mathbf{K}^{-1}\mathbf{v}_i\] \[\mathbf{v}_i^T\mathbf{K}^{-T}\mathbf{K}^{-1}\mathbf{v}_j = 0, \quad i \neq j\]

这个约束只包含内参矩阵\(\mathbf{K}\)。

求解内参

假设\(\mathbf{K} = \begin{bmatrix} f & 0 & c_x \\ 0 & f & c_y \\ 0 & 0 & 1 \end{bmatrix}\)（简化模型，3个参数）

约束方程数：

• 3对消失点产生3个正交约束

\[\mathbf{v}_i^T\mathbf{K}^{-T}\mathbf{K}^{-1}\mathbf{v}_j = 0\]

展开\(\mathbf{K}^{-1}\)和\(\mathbf{K}^{-T}\)：

\[\mathbf{K}^{-1} = \begin{bmatrix} g & 0 & -gc_x \\ 0 & g & -gc_y \\ 0 & 0 & 1 \end{bmatrix}, \quad g = \frac{1}{f}\] \[\mathbf{K}^{-T} = \begin{bmatrix} g & 0 & 0 \\ 0 & g & 0 \\ -gc_x & -gc_y & 1 \end{bmatrix}\]

对于\(\mathbf{v}_i = (x_i, y_i, w_i)^T\)：

\[\mathbf{v}_i^T\mathbf{K}^{-T}\mathbf{K}^{-1}\mathbf{v}_j = g^2(x_ix_j + y_iy_j) - g^2c_x(w_ix_j + w_jx_i) - g^2c_y(w_iy_j + w_jy_i) + g^2(c_x^2 + c_y^2)w_iw_j + w_iw_j = 0\]

这是关于\(g, c_x, c_y\)的非线性方程，但可以求解。

要求：至少两个有限消失点才能同时求解\(f\)和\((c_x, c_y)\)。

不同配置的影响：

• 1个有限消失点 + 2个无限消失点：只能求解焦距，主点位置无法确定（假设为图像中心）
• 2个有限消失点 + 1个无限消失点：可以同时求解焦距和主点位置
• 3个有限消失点：过约束系统，可以更鲁棒地求解所有参数

从消失点恢复旋转

已知\(\mathbf{K}\)后，恢复旋转矩阵\(\mathbf{R}\)：

\[\mathbf{K}^{-1}\mathbf{v}_i \cong \mathbf{R}\mathbf{e}_i\]

注意到\(\mathbf{R}\mathbf{e}_1 = \begin{bmatrix} \mathbf{r}_1 & \mathbf{r}_2 & \mathbf{r}_3 \end{bmatrix}\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} = \mathbf{r}_1\)

因此：\(\mathbf{r}_i \cong \mathbf{K}^{-1}\mathbf{v}_i\)

尺度歧义通过正交性约束消除：\(\|\mathbf{r}_i\|^2 = 1\)

最终得到：\(\mathbf{r}_i = \frac{\mathbf{K}^{-1}\mathbf{v}_i}{\|\mathbf{K}^{-1}\mathbf{v}_i\|}\)

消失点标定的优缺点

优点：

• 无需标定板
• 无需2D-3D对应关系
• 可以完全自动化

缺点：

• 只适用于特定场景（需要正交消失方向）
• 消失点定位精度影响标定结果
• 至少需要两个有限消失点

6.11 总结

3D视觉的关键问题

从图像重建3D结构的核心是解决单视图歧义性。

主要方法：

1. 主动传感（激光、结构光）
2. 立体视觉（双目）
3. 多视图几何（运动恢复结构）
4. 形状从明暗
5. 深度学习

相机标定

相机矩阵：\(\mathbf{x} \cong \boldsymbol{\Pi}\mathbf{X} = \mathbf{K}[\mathbf{R} \mid \mathbf{t}]\mathbf{X}\)

线性标定：

• 给定\(n \geq 6\)个3D-2D对应点
• 构造线性方程组\(\mathbf{A}\mathbf{p} = \mathbf{0}\)
• 通过特征值分解求解
• 使用RQ分解恢复\(\mathbf{K}, \mathbf{R}, \mathbf{t}\)

非线性标定（实际更常用）：

• 最小化几何误差（重投影误差）
• 可以加入畸变参数
• 用线性方法初始化

消失点标定：

• 利用场景中的正交消失方向
• 通过正交约束求解内参
• 适用于建筑物等人造环境

三角测量

给定已知相机矩阵和对应点，求3D点坐标。

方法：

1. 几何方法：找最短连接线段的中点
2. 非线性优化：最小化重投影误差
3. 线性方法：利用叉积约束，特征值分解

实际应用：两条视线通常不精确相交，需要鲁棒估计。

关键技术要点

• 齐次坐标：统一处理各种变换和投影
• RQ分解：从相机矩阵恢复内外参
• 特征值分解：求解线性约束最小化问题
• 几何误差vs代数误差：非线性优化更准确
• 正交约束：用于消失点标定和旋转矩阵恢复

参考文献：Computer Vision: Algorithms and Applications, 第11章