CV - 5: 图像拼接 (Image Stitching)

5.1 全景图概述

全景图像拼接是计算机视觉中的经典应用，旨在将多张有重叠部分的图像拼接成一张宽视角的全景图像。

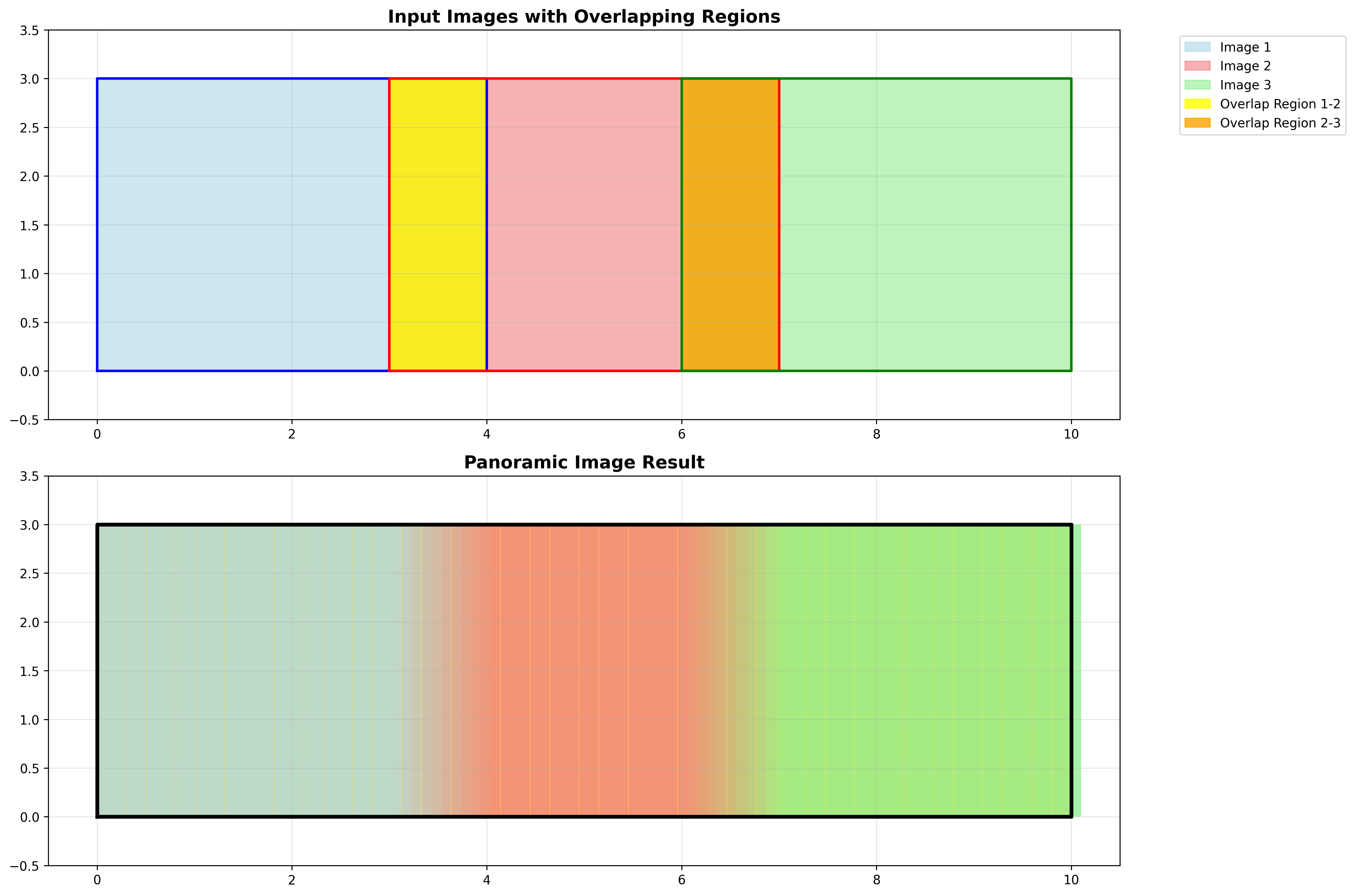
全景图构建流程

构建全景图的主要步骤包括：

特征点提取（Extract feature points）
特征匹配（Feature matching）
求解变换矩阵（Solve transformations）
图像融合（Blend images）

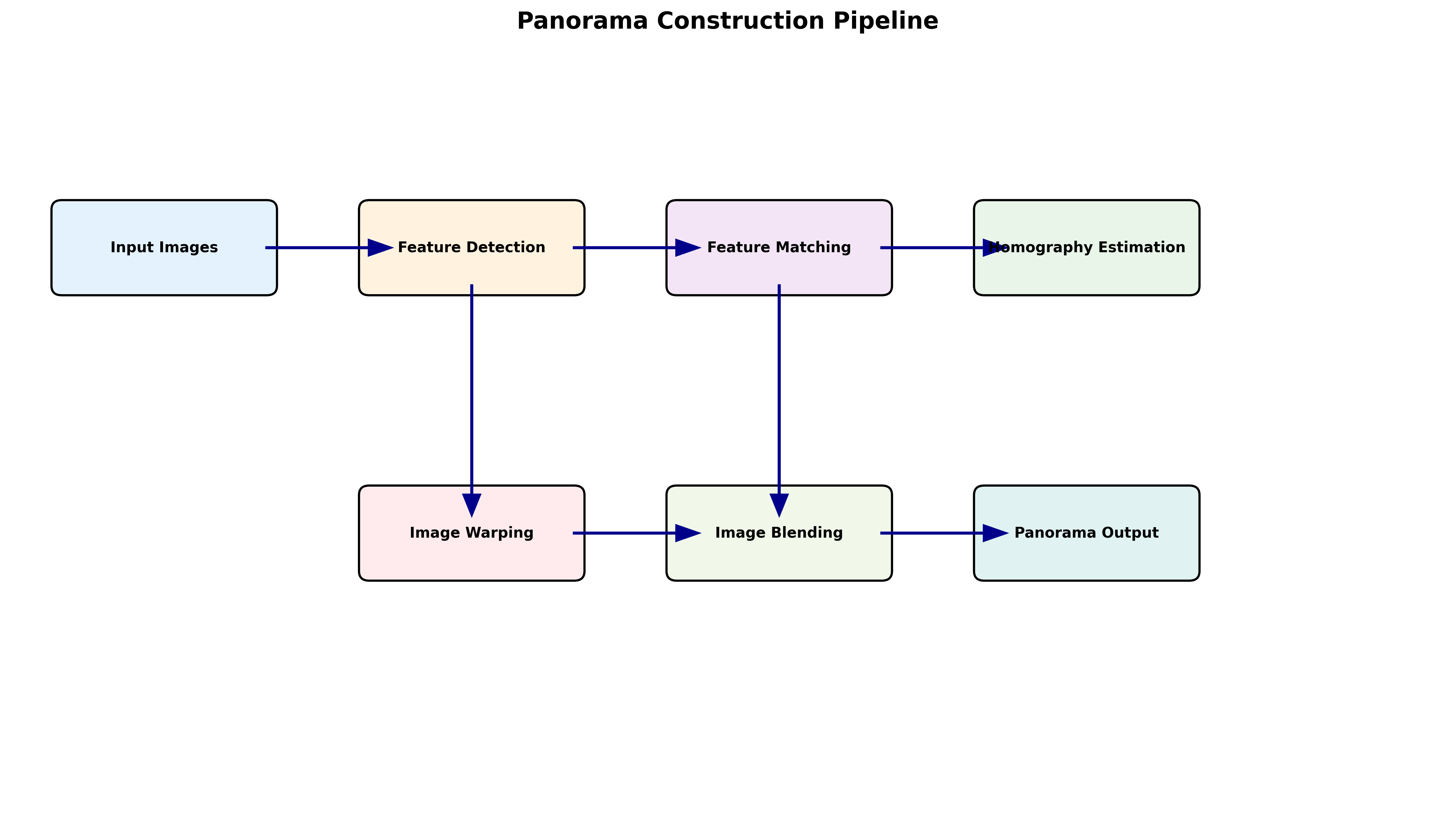
5.2 图像变换回顾

图像变换的分类

图像滤波：改变图像的值域 $g(x) = T(f(x))$

图像变形：改变图像的定义域 $g(x) = f(T(x))$

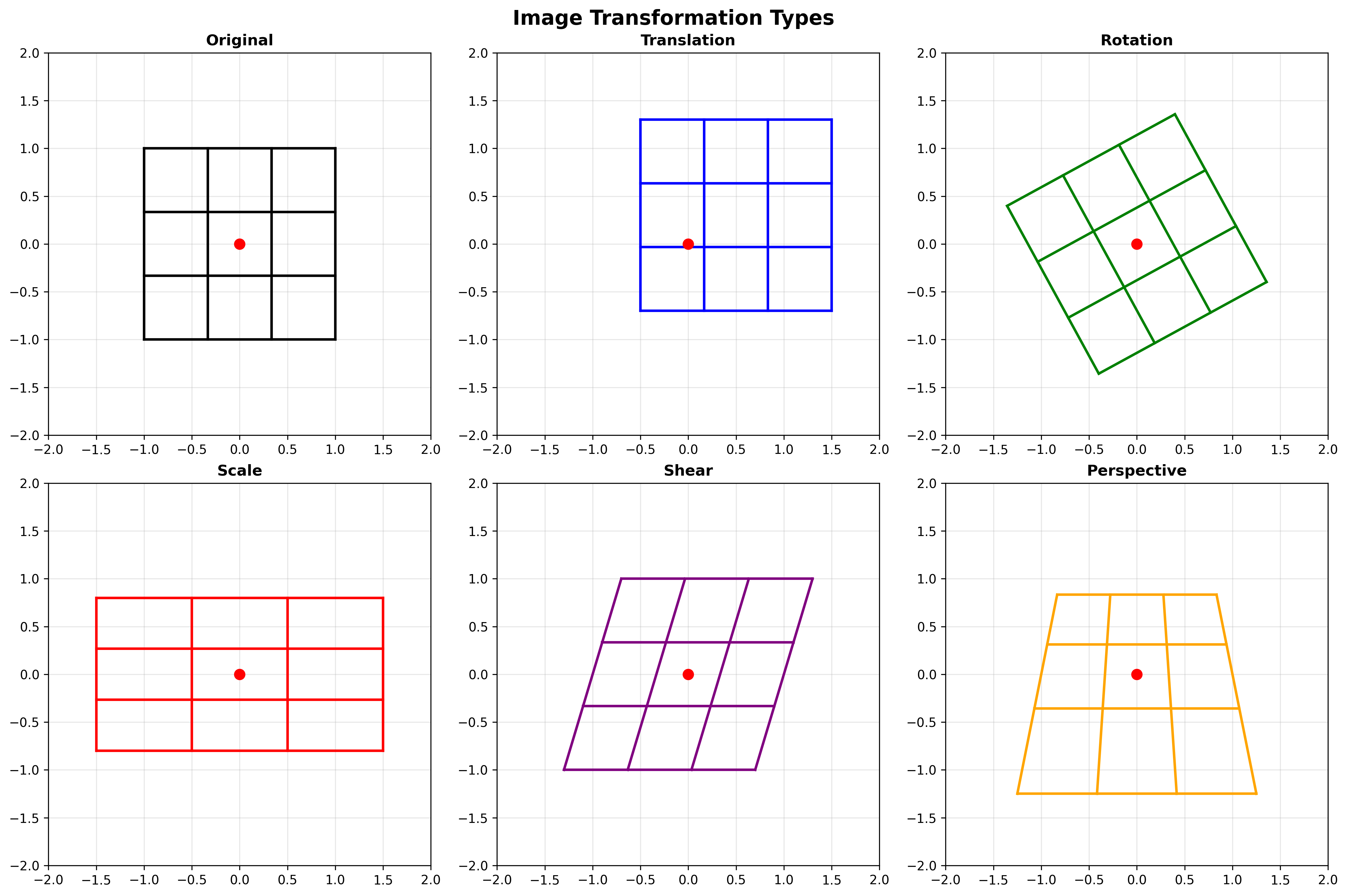
全局图像变形示例

常见的全局图像变形包括：

平移（Translation）
旋转（Rotation）
缩放（Scale）
仿射变换（Affine）
透视变换（Perspective）
圆柱投影（Cylindrical）

变换的通用形式：$p' = T(p)$

其中$T$对所有点都相同，且不依赖于图像内容；$p$和$p'$为2D像素坐标。

5.3 齐次坐标与变换矩阵

齐次坐标系统

齐次坐标将2D点$(x,y)$表示为3D向量： $\begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \Rightarrow \begin{bmatrix} x \\ y \\ w \end{bmatrix} \Rightarrow (x/w, y/w)$

仿射变换

使用齐次坐标的仿射变换： $\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} \equiv \begin{bmatrix} a & b & c \\ d & e & f \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \equiv T \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

对应于非齐次坐标形式：$x' = Ax + b$

自由度：6

基本变换类型

平移变换（自由度：2）： $\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

旋转变换（自由度：1）： $\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

缩放变换（自由度：2）： $\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

剪切变换（自由度：2）： $\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & sh_x & 0 \\ sh_y & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

5.4 仿射变换的求解

建立方程组

给定对应点对：$[x_i', y_i'] \leftrightarrow [x_i, y_i]$

每个点对建立2个方程： $\begin{bmatrix} x_i' \\ y_i' \end{bmatrix} = \begin{bmatrix} a & b \\ d & e \end{bmatrix} \begin{bmatrix} x_i \\ y_i \end{bmatrix} + \begin{bmatrix} c \\ f \end{bmatrix}$

矩阵形式： $\begin{bmatrix} \vdots \\ x_i' \\ y_i' \\ \vdots \end{bmatrix} = \begin{bmatrix} \cdots \\ x_i & y_i & 0 & 0 & 1 & 0 \\ 0 & 0 & x_i & y_i & 0 & 1 \\ \cdots \end{bmatrix} \begin{bmatrix} a \\ b \\ d \\ e \\ c \\ f \end{bmatrix}$

即：$b_{2n \times 1} = A_{2n \times 6} t_{6 \times 1}$

最小二乘解

所需点数：3个不共线的点（6个约束，6个未知数）
实际应用：通常有更多对应点
优化目标：最小化重投影误差

\[E = ||At - b||_2^2 = t^T A^T A t - 2t^T A^T b + b^T b\]

解：$t = (A^T A)^{-1} A^T b$

5.5 单应性变换（Homography）

单应性的定义

当图像间的变换不是仿射变换时（如透视变换），需要使用单应性：

\[\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} \cong \begin{bmatrix} h_{00} & h_{01} & h_{02} \\ h_{10} & h_{11} & h_{12} \\ h_{20} & h_{21} & h_{22} \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}\]

特点：

$3 \times 3$矩阵
最后一行为$[g, h, i]$，而非$[0, 0, 1]$
也称为投影变换
自由度：8

单应性的几何意义

单应性描述了以下两种情况下的图像变换：

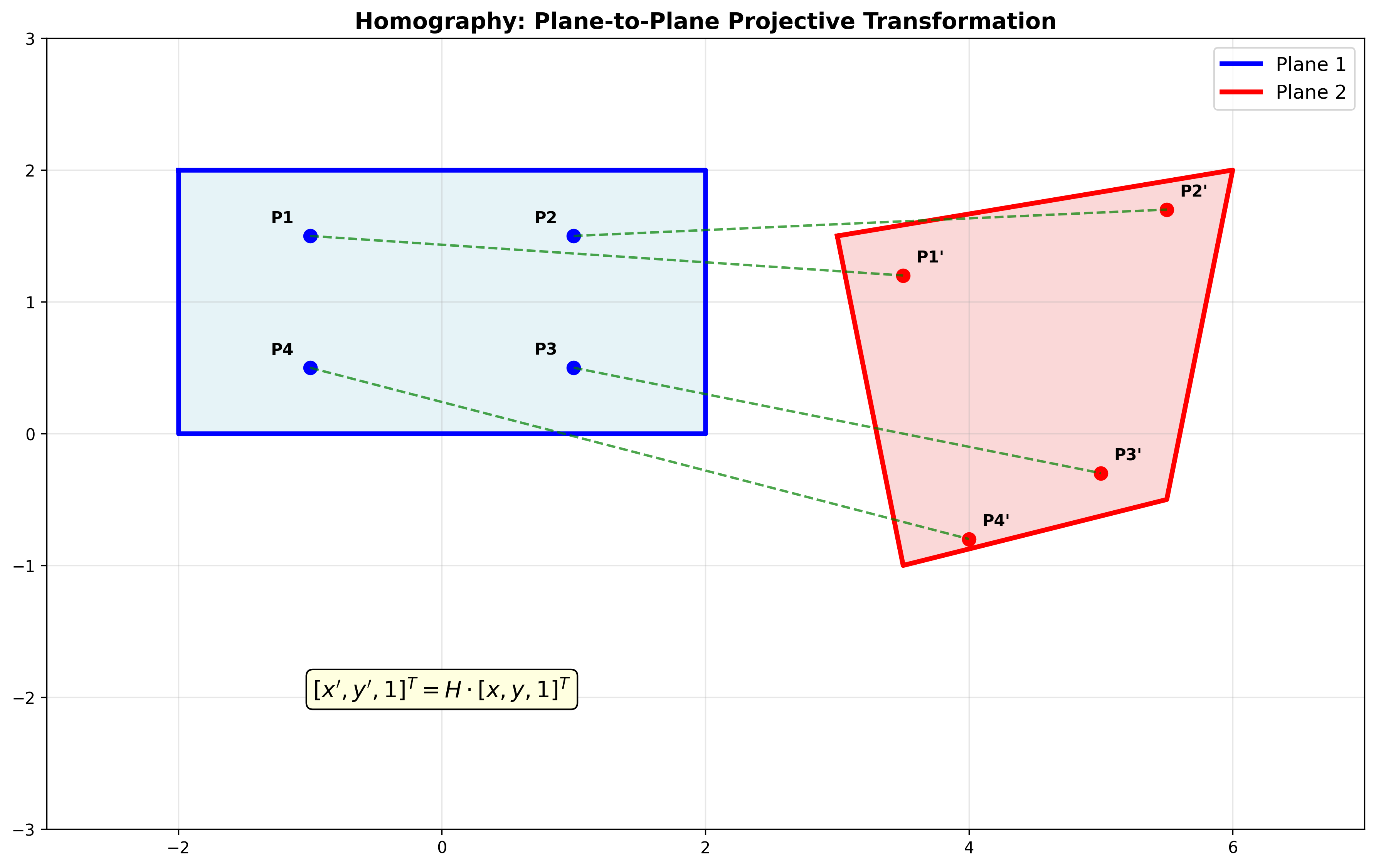
平面表面的两个视角之间的变换
共享相同中心的两个相机之间的变换

现实世界中的单应性

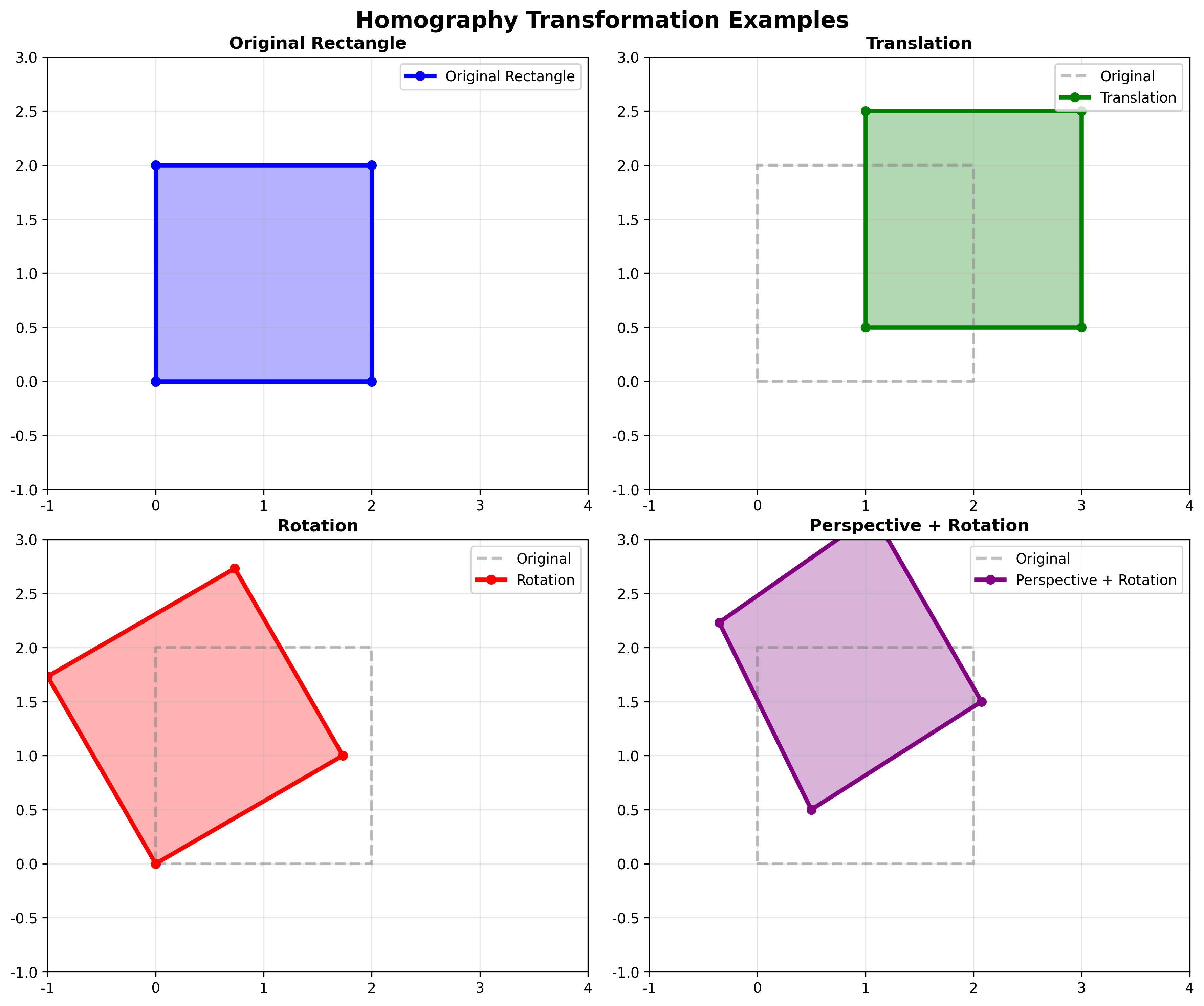
5.6 单应性的求解

数学推导

给定对应点：$[x_i', y_i'] \leftrightarrow [x_i, y_i]$

单应性变换： $x_i' = \frac{h_{00}x_i + h_{01}y_i + h_{02}}{h_{20}x_i + h_{21}y_i + h_{22}}$ $y_i' = \frac{h_{10}x_i + h_{11}y_i + h_{12}}{h_{20}x_i + h_{21}y_i + h_{22}}$

交叉乘积形式： $x_i'(h_{20}x_i + h_{21}y_i + h_{22}) = h_{00}x_i + h_{01}y_i + h_{02}$ $y_i'(h_{20}x_i + h_{21}y_i + h_{22}) = h_{10}x_i + h_{11}y_i + h_{12}$

线性方程组

每个点对产生2个线性方程： $\begin{bmatrix} x_1 & y_1 & 1 & 0 & 0 & 0 & -x_1'x_1 & -x_1'y_1 & -x_1' \\ 0 & 0 & 0 & x_1 & y_1 & 1 & -y_1'x_1 & -y_1'y_1 & -y_1' \\ \vdots & & & & & & & & \vdots \\ x_n & y_n & 1 & 0 & 0 & 0 & -x_n'x_n & -x_n'y_n & -x_n' \\ 0 & 0 & 0 & x_n & y_n & 1 & -y_n'x_n & -y_n'y_n & -y_n' \end{bmatrix} \begin{bmatrix} h_{00} \\ h_{01} \\ h_{02} \\ h_{10} \\ h_{11} \\ h_{12} \\ h_{20} \\ h_{21} \\ h_{22} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \\ 0 \end{bmatrix}$

即：$A_{2n \times 9} h_9 = 0_{2n}$

约束最小化

所需点数：4个不共线的点

约束条件：$$

^2 = 1$$

优化问题： $E = ||Ah||^2 + \lambda(||h||^2 - 1) = h^T A^T A h + \lambda h^T h - \lambda$

解：$A^T A h = \lambda h$

$h$是$A^T A$最小特征值对应的特征向量。

代数误差 vs 几何误差

代数误差：$$

^2$$

几何误差： $\sum_{i=1}^k ||[x_i', y_i'] - T([x_i, y_i])||^2 + ||[x_i, y_i] - T^{-1}([x_i', y_i'])||^2$

5.7 特征匹配与外点处理

特征匹配流程

计算图像A和B的特征
使用最近邻搜索匹配特征
在匹配集上计算单应性
问题：匹配中存在外点（outliers）

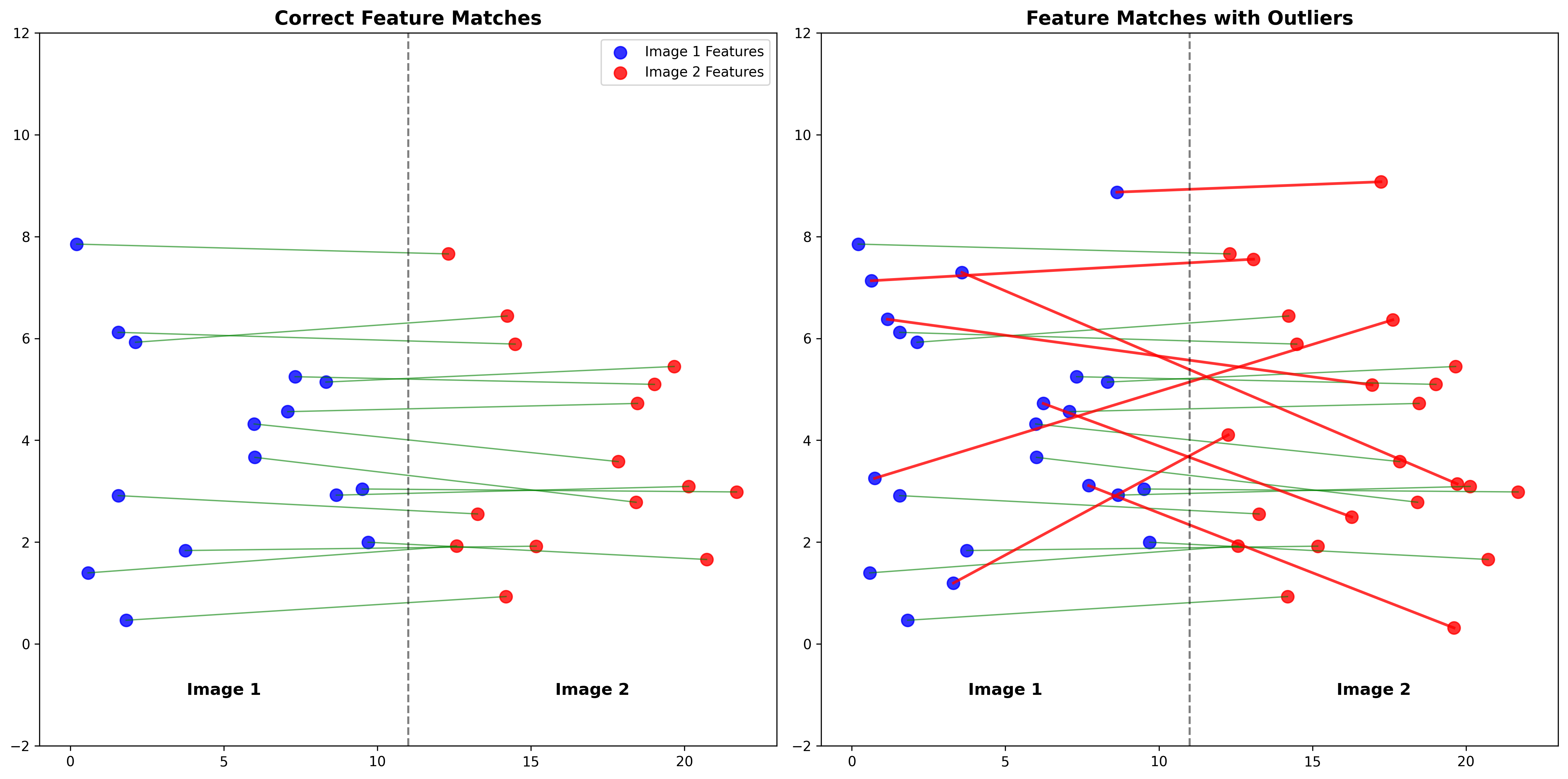
外点的影响

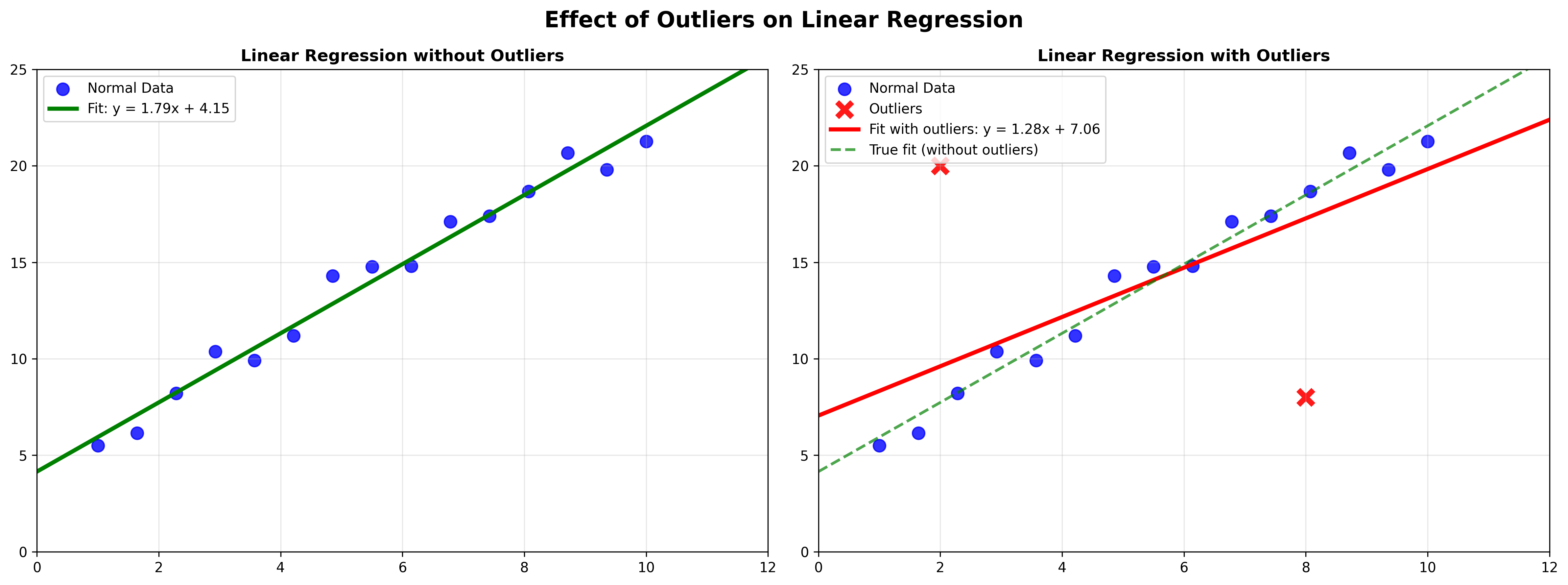
线性回归示例：

模型：$y = ax + b$
目标函数：$E = \sum_i (ax_i + b - y_i)^2$
问题：大量外点导致结果偏离真实值

5.8 RANSAC算法

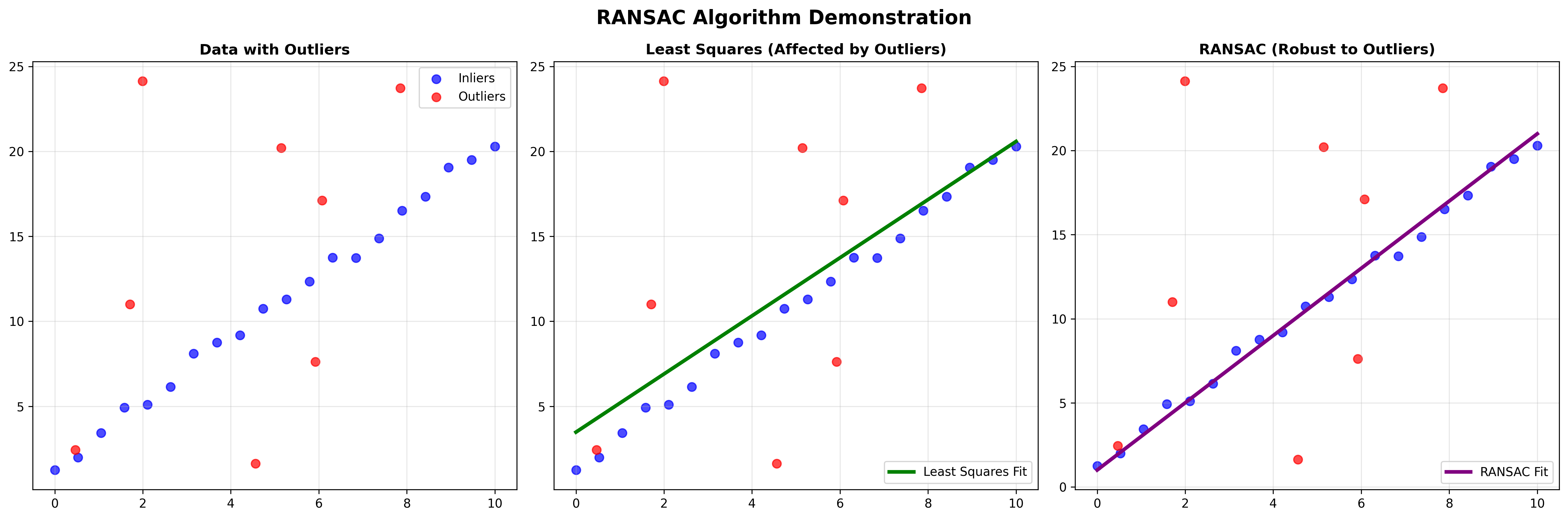
RANSAC基本思想

RANSAC（RANdom SAmple Consensus）是一种鲁棒估计算法：

随机选择$s$个样本点
- 通常$s$是拟合模型的最小样本数
拟合模型到这些样本
计算内点数量（满足模型的点）
重复$N$次
选择内点最多的模型
用所有内点重新拟合最终模型

内点判别

使用几何误差阈值判别内点：

拟合模型后，计算每个点到模型的几何距离
距离小于阈值的点为内点
对于单应性，使用重投影误差作为几何误差

迭代次数确定

设：

$G$：内点比例
$P$：模型所需点数
$N$：迭代次数

N次迭代后仍未选到全内点集的概率：$(1-G^P)^N$

失败概率上界$e$的迭代次数： $N > \frac{\log e}{\log(1-G^P)}$

示例：

$G = 50\%, P = 4, N = 100$：失败概率 ≈ 0.16%
$G = 30\%, P = 4, N = 1000$：失败概率 ≈ 0.03%

RANSAC的优缺点

优点：

简单通用
适用于多种问题
实际效果良好

缺点：

参数需要调节
内点比例低时可能失败
需要大量迭代

其他方法：鲁棒统计学方法

5.9 图像融合

拉普拉斯金字塔融合

核心思想：

低频成分在较大空间范围内融合
高频成分在较小空间范围内融合

问题：长距离融合可能混合两个图像的内容

泊松图像编辑

动机：源图像的色调与目标图像不兼容

核心思想：保持源图像的梯度

优化目标： $E = \min_f \sum_{(i,j) \in \Omega} ||\nabla f(i,j) - \nabla g(i,j)||_2^2$

边界条件： $f(i,j) = f^*(i,j) \text{ for } (i,j) \in \partial\Omega$

其中：

$g$：源图像
$f^*$：目标图像
$f$：输出图像
$\Omega$：融合区域

泊松方程求解

梯度的矩阵形式： $\nabla = \begin{pmatrix} -1 & 1 & \cdots & 0 & 0 \\ 0 & -1 & & 0 & 0 \\ \vdots & & \ddots & & \vdots \\ 0 & 0 & & -1 & 1 \\ 0 & 0 & \cdots & 0 & -1 \end{pmatrix}$

最小二乘问题： $\min_f ||Af - G||^2 + \lambda||Bf - F||^2$

解： $(A^T A + \lambda B^T B)f = b$

这是一个大规模稀疏线性系统。

泊松编辑的全景图应用

步骤：

求解单应性矩阵
将源图像变形到参考图像
将掩膜变形到参考图像
在掩膜区域运行泊松编辑算法

5.10 总结

全景图构建完整流程

特征点提取：检测关键点和描述符
特征匹配：最近邻搜索建立对应关系
求解变换：
- 使用RANSAC处理外点
- 估计单应性矩阵（8自由度）
- 最少需要4个不共线点对
图像融合：
- 拉普拉斯金字塔融合
- 泊松图像编辑

关键技术要点

齐次坐标：统一处理各种变换
单应性：描述平面到平面的投影变换
RANSAC：鲁棒估计处理外点
几何误差：比代数误差更准确的质量度量
多尺度融合：自然的图像拼接效果

参考文献：Computer Vision教材第8章