CV - 4: 特征检测 (Feature Detection)

边缘检测 (Edge Detection)

边缘的定义与重要性

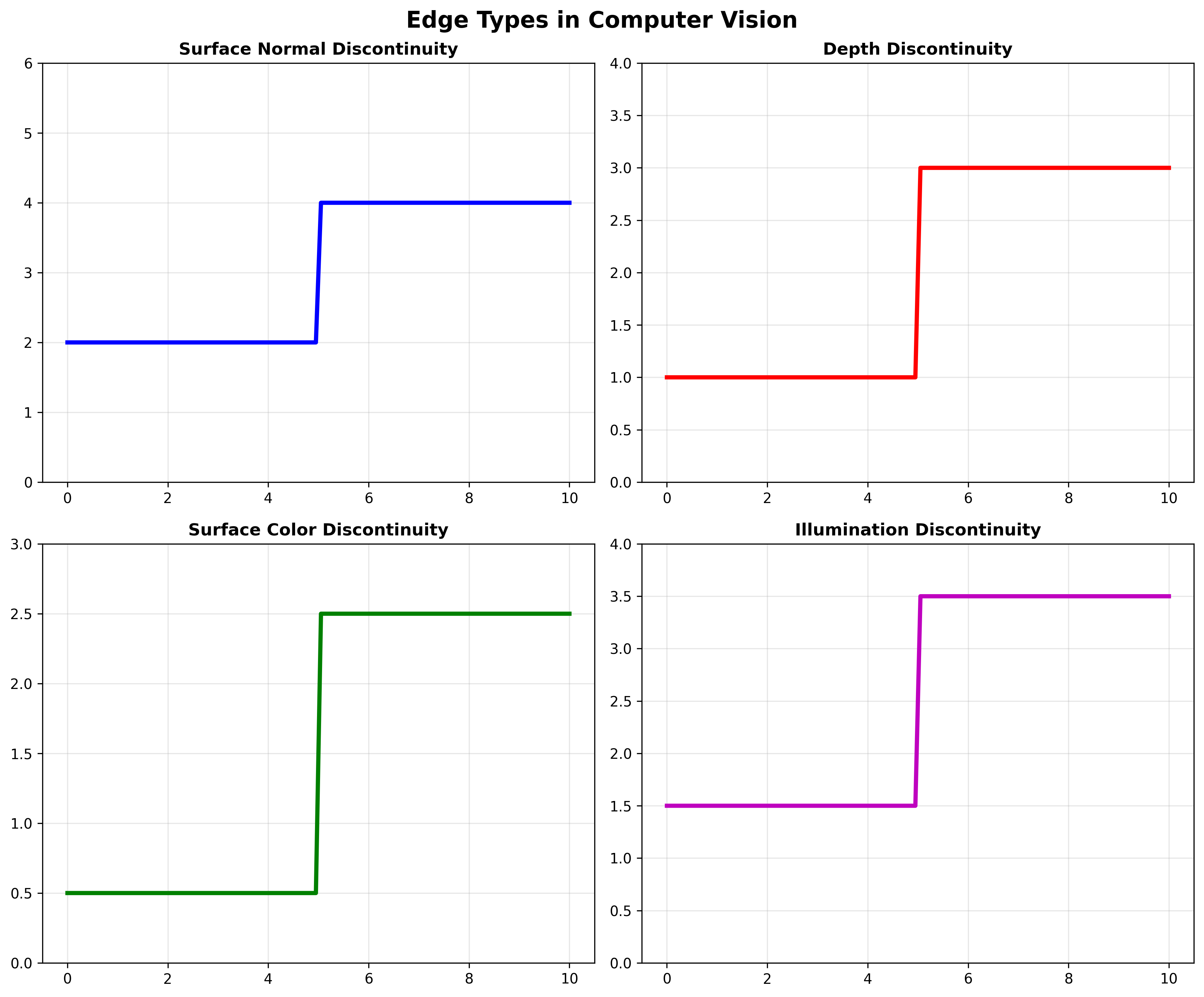
边缘包含了图像中大部分的语义和形状信息。边缘检测的目标是识别图像中的突然变化（不连续性），这些不连续性可能来自：

表面法线不连续
深度不连续
表面颜色不连续
光照不连续

边缘检测的数学基础

边缘对应于导数的极值点。对于图像函数 $I(x,y)$：

X方向偏导数： $\frac{\partial I(x,y)}{\partial x} = \lim_{\epsilon \to 0} \frac{I(x+\epsilon,y) - I(x,y)}{\epsilon}$

前向差分： $\frac{\partial I(x,y)}{\partial x} \approx \frac{I(x+1,y) - I(x,y)}{1}$

中央差分： $\frac{\partial I(x,y)}{\partial x} \approx \frac{I(x+1,y) - I(x-1,y)}{2}$

图像偏导数的滤波器实现

图像的偏导数可以通过图像滤波来计算：

Prewitt算子：

水平方向：$\begin{bmatrix} -1 & 0 & 1 \ -1 & 0 & 1 \ -1 & 0 & 1 \end{bmatrix}$
垂直方向：$\begin{bmatrix} 1 & 1 & 1 \ 0 & 0 & 0 \ -1 & -1 & -1 \end{bmatrix}$

Sobel算子：

水平方向：$\begin{bmatrix} -1 & 0 & 1 \ -2 & 0 & 2 \ -1 & 0 & 1 \end{bmatrix}$
垂直方向：$\begin{bmatrix} 1 & 2 & 1 \ 0 & 0 & 0 \ -1 & -2 & -1 \end{bmatrix}$

噪声对导数的影响

噪声会严重影响图像导数的计算。设真实图像为 $I_{i,j}$，噪声为 $\epsilon_{i,j} \sim N(0,\sigma^2)$：

\[D_{i,j} = (I_{i,j+1} + \epsilon_{i,j+1}) - (I_{i,j-1} + \epsilon_{i,j-1})\] \[= (I_{i,j+1} - I_{i,j-1}) + \epsilon_{i,j+1} - \epsilon_{i,j-1}\]

由于 $\epsilon_{i,j} - \epsilon_{k,l} \sim N(0, 2\sigma^2)$，噪声的方差会翻倍！

解决方案： 先用高斯滤波器对图像进行预滤波，然后计算导数。

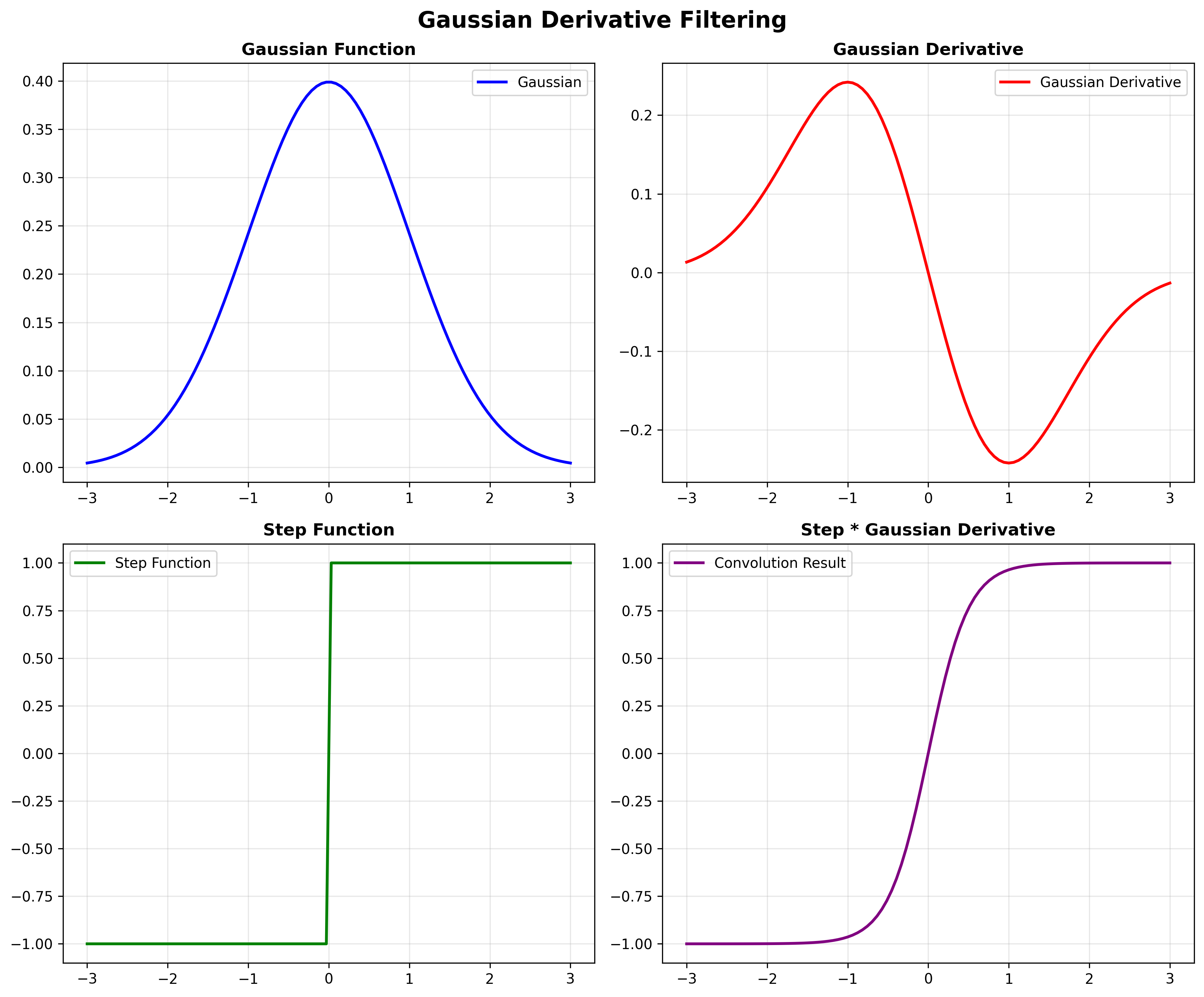
高斯导数滤波

利用卷积的性质： $\frac{d}{dx}(f * g) = f * \frac{d}{dx}g$

可以直接用高斯导数滤波器进行一次卷积操作。

图像梯度

图像梯度定义为： $\nabla f = \begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix}$

梯度幅值： $ \nabla f = \sqrt{(\frac{\partial f}{\partial x})^2 + (\frac{\partial f}{\partial y})^2}$
梯度方向： $\theta = \tan^{-1}(\frac{\partial f}{\partial y} / \frac{\partial f}{\partial x})$

梯度指向强度增长最快的方向。

Canny边缘检测器

Canny边缘检测是一个多步骤的边缘检测算法：

步骤1：预处理

灰度化转换
高斯模糊去噪

步骤2：计算梯度

使用中央差分（如Sobel算子）计算x和y方向的梯度，然后计算梯度幅值。

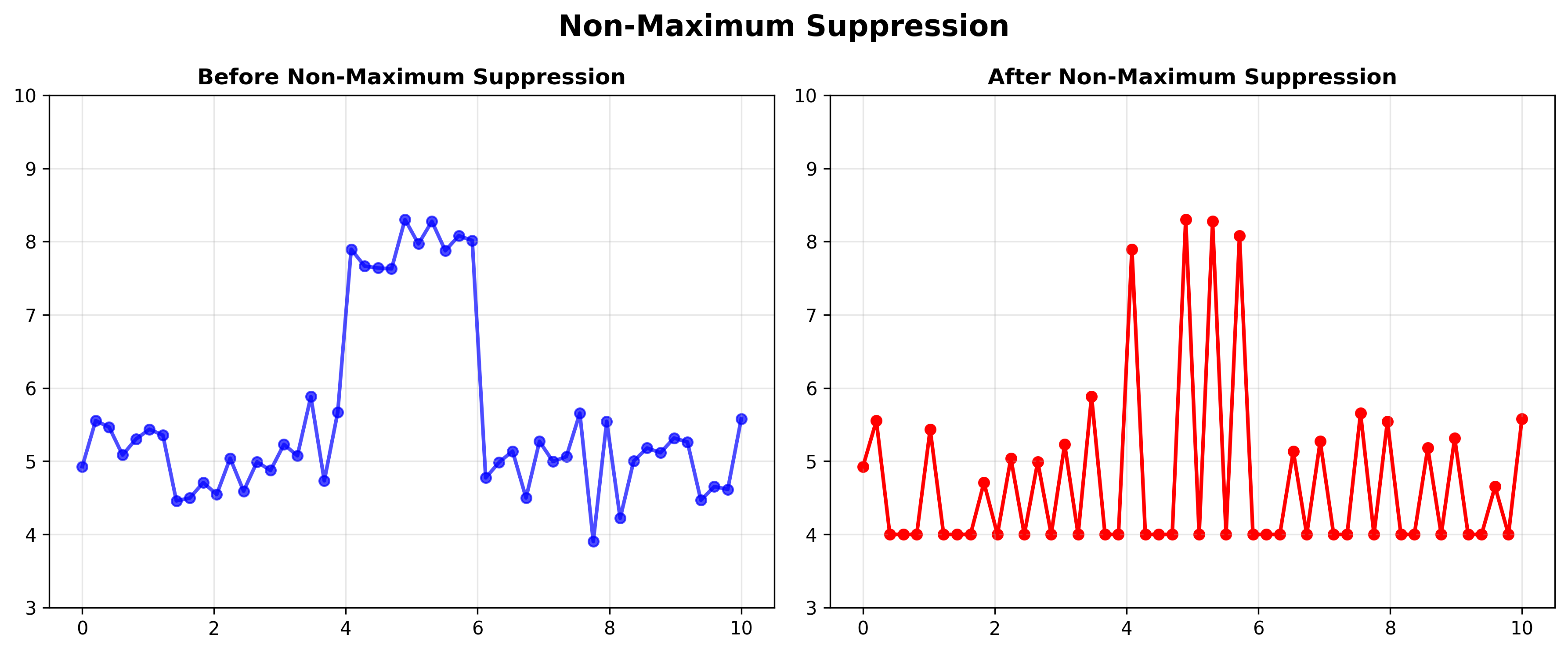
步骤3：非最大值抑制

梯度幅值产生的边缘太粗，需要进行非最大值抑制来细化边缘：

沿梯度方向检查邻近像素
只保留在边缘方向上具有最大值的像素
例如：保持 $q$ 当 $q > p$ 且 $q > r$ 时

步骤4：双阈值处理

高阈值（如0.7）：强边缘候选
低阈值（如0.3）：弱边缘候选
中间值：待定边缘

步骤5：边缘跟踪（滞后处理）

连接到强边缘的弱边缘被保留为真实边缘
不连接到强边缘的弱边缘被删除

角点检测 (Corner Detection)

角点的重要性

边缘难以精确定位，而角点可以被精确定位且更具判别性。角点是两条或多条边缘的交点。

Harris角点检测器

Harris角点检测的核心思想：通过测量移动小窗口时的强度变化来表征角点。

强度变化函数： $E(u,v) = \sum_{(x,y) \in W} w(x,y)[I(x+u,y+v) - I(x,y)]^2$

泰勒级数近似

使用泰勒级数将图像函数线性化： $I(x+u,y+v) \approx I(x,y) + I_x u + I_y v$

其中 $I_x = \frac{\partial I}{\partial x}$，$I_y = \frac{\partial I}{\partial y}$

二阶矩矩阵

将强度变化函数简化为二次型： $E(u,v) = [u,v] \mathbf{M} [u,v]^T$

其中二阶矩矩阵 $\mathbf{M}$ 为：

\[\mathbf{M} = \begin{bmatrix} \sum I_x^2 & \sum I_x I_y \\ \sum I_x I_y & \sum I_y^2 \end{bmatrix}\]

特征值解释

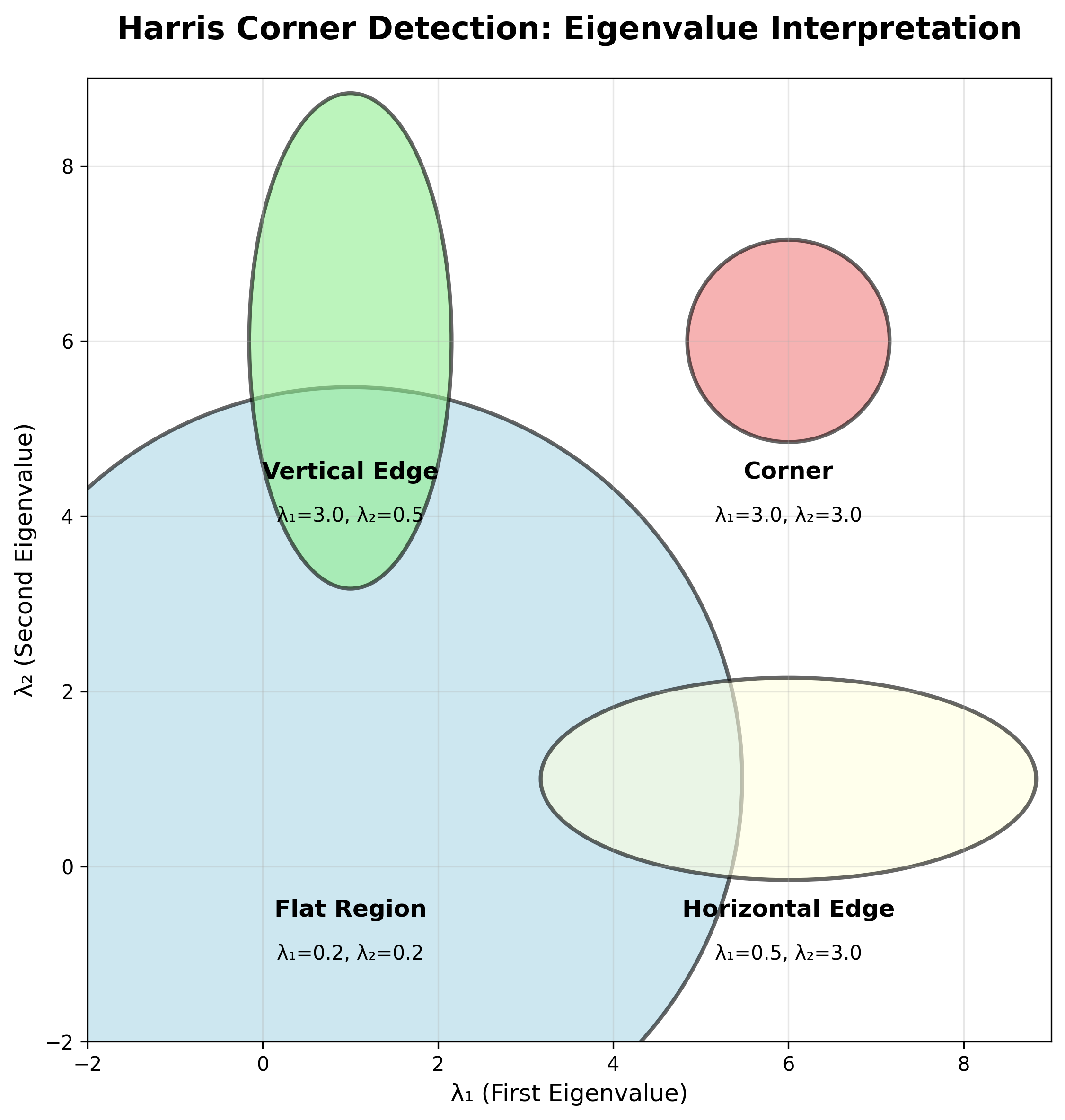
通过分析矩阵 $\mathbf{M}$ 的特征值 $\lambda_1$ 和 $\lambda_2$：

平坦区域： $\lambda_1$ 和 $\lambda_2$ 都很小，$E$ 在所有方向几乎不变
边缘： $\lambda_1 » \lambda_2$ 或 $\lambda_2 » \lambda_1$，$E$ 沿边缘方向不变
角点： $\lambda_1$ 和 $\lambda_2$ 都很大且 $\lambda_1 \sim \lambda_2$，$E$ 在所有方向都增加

Harris响应函数

为避免计算特征值，使用Harris响应函数： $R = \det(\mathbf{M}) - \alpha \cdot \text{trace}(\mathbf{M})^2$ $= \lambda_1 \lambda_2 - \alpha(\lambda_1 + \lambda_2)^2$

其中 $\alpha$ 是常数（通常取0.04-0.06）。

Harris角点检测步骤

预处理： 转换为灰度图并应用高斯滤波
梯度计算： 应用Sobel算子找到x和y梯度值
Harris值计算： 对每个像素，考虑3×3窗口计算二阶矩矩阵和角点强度函数R
阈值处理和非最大值抑制

角点的性质

平移等变： 卷积运算具有平移不变性
旋转等变： 旋转只会改变角点的旋转，特征值保持不变
仿射强度变化部分不变： 对于 $I_{new} = \alpha I_{old} + \beta$，$\beta$ 不影响导数，但 $\alpha$ 会缩放导数
尺度不等变： 一个像素可能变成多个像素，角点不具有尺度等变性

多尺度角点检测

使用高斯金字塔在多个尺度上执行Harris检测，使角点具有尺度等变性。

Blob检测

Blob的定义

Blob是数字图像中在亮度或颜色等属性上与周围区域不同的区域。Blob具有固定的位置和大小，可以被定位，是良好的兴趣点。

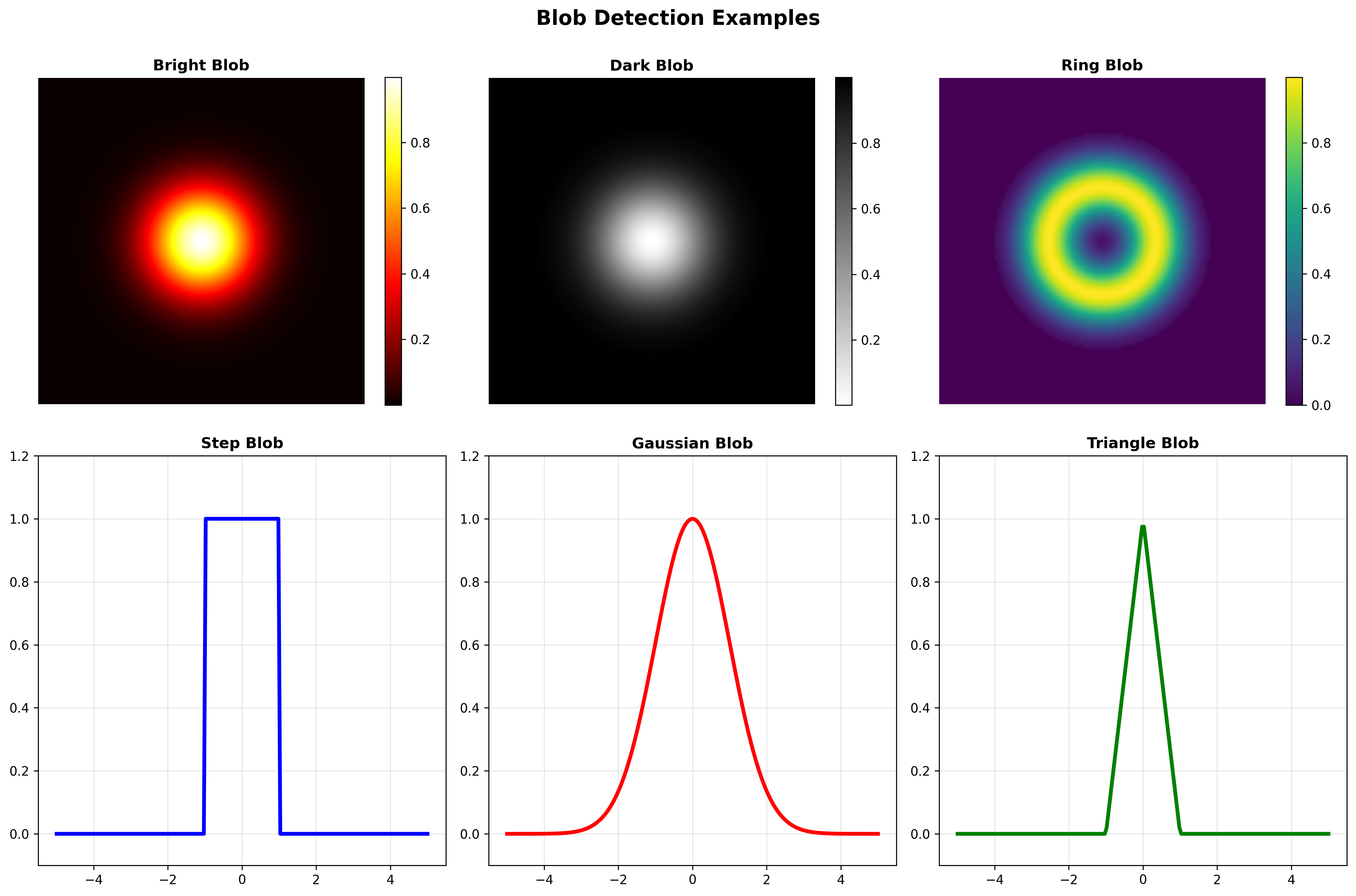
2D Blob检测理论

二维空间中的Laplacian of Gaussian：

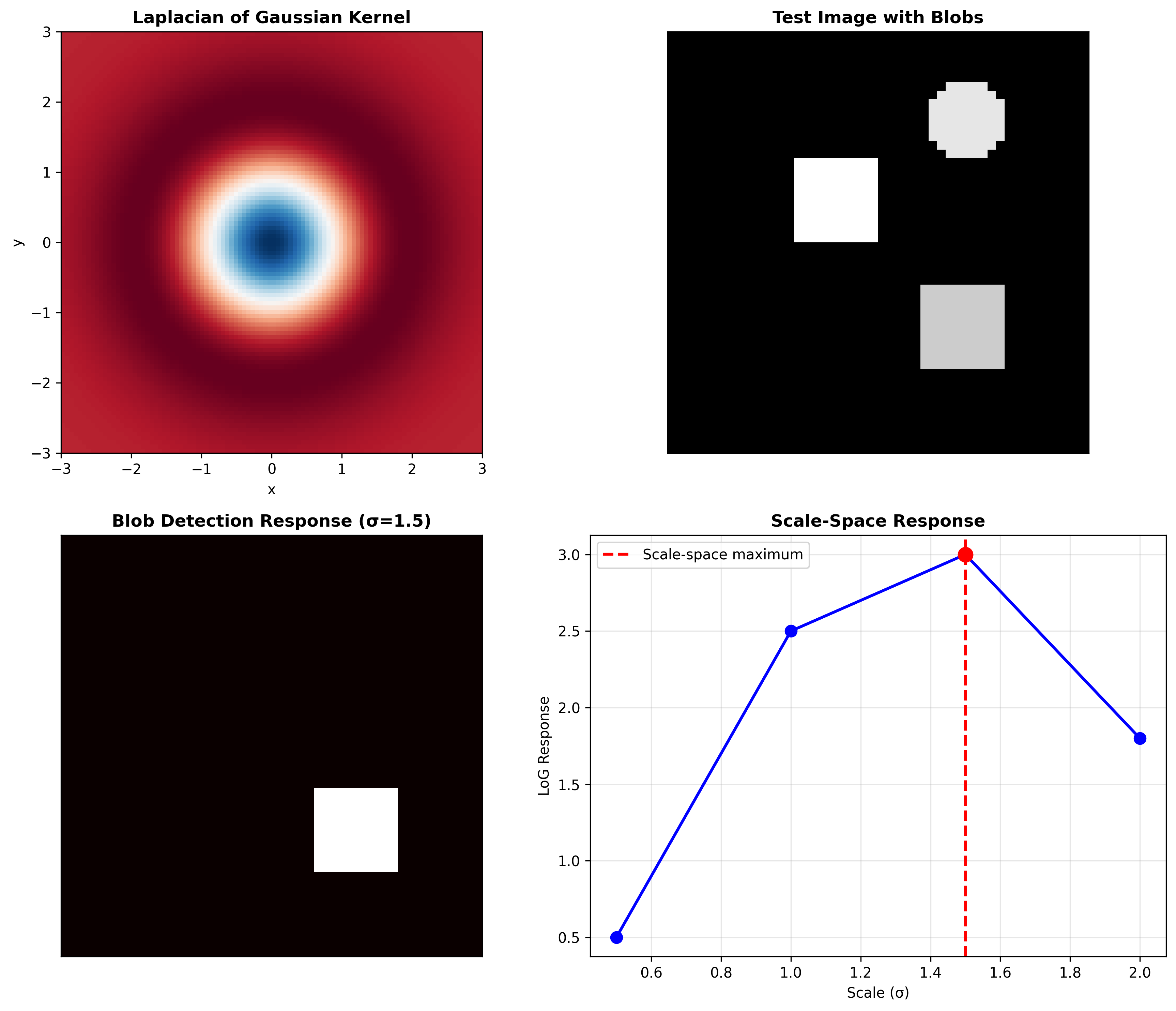
在2D图像中，LoG算子的完整表达式为：

\[\nabla^2 G_\sigma = \frac{1}{\pi \sigma^4} \left(1 - \frac{x^2 + y^2}{2\sigma^2}\right) e^{-\frac{x^2 + y^2}{2\sigma^2}}\]

多尺度blob检测步骤：

在多个尺度 $\sigma$ 上计算LoG响应
在3D空间（x, y, σ）中寻找局部最大值
最优检测尺度：blob半径 ≈ $\sqrt{2}\sigma$

点和边缘的局限性

边缘难以定位
点可以定位，但缺乏判别性

Blob检测常用于获得感兴趣区域以供进一步处理，是著名SIFT特征的前身。

高斯导数的边缘检测

对于卷积运算： $\frac{d}{dx}[f * h] = \frac{d}{dx} \int f(\tau)h(x-\tau)d\tau = f * \frac{dh}{dx} = \frac{df}{dx} * h$

对于阶跃函数 $f(x) = u(x-x_0)$ 和高斯函数 $h(x) = G_\sigma(x)$： $(f * h)' = f * h' = f' * h = G_\sigma(x) * \delta(x-x_0) = G_\sigma(x-x_0)$

边缘位于 $x_0$ 处。使用归一化高斯导数 $\sigma G_\sigma’$ 使极值不依赖于 $\sigma$。

高斯二阶导数的边缘检测

$f * h’$ 的极值点是边缘 → $f * h’’$ 的零交叉点是边缘

对于阶跃函数和高斯函数的卷积： $u(x-x_0) * \frac{d^2G_\sigma(x)}{dx^2} = \frac{-(x-x_0)}{\sqrt{2\pi\sigma^3}} e^{-\frac{(x-x_0)^2}{2\sigma^2}}$

响应在 $x = x_0$ 时为0。使用归一化二阶高斯导数 $\sigma^2 G_\sigma’’$ 使极值不依赖于 $\sigma$。

1D Blob检测与高斯二阶导数

定义1D Blob为：$f(x) = u(x-x_0) - u(x-x_1)$

用归一化高斯二阶导数滤波： $f(x) * \sigma^2 \frac{d^2G_\sigma(x)}{dx^2} = -\frac{(x-x_0)}{\sqrt{2\pi\sigma}} e^{-\frac{(x-x_0)^2}{2\sigma^2}} + \frac{(x-x_1)}{\sqrt{2\pi\sigma}} e^{-\frac{(x-x_1)^2}{2\sigma^2}}$

当 $\sigma = \frac{x_1-x_0}{2}$ 时，极值重合在 $x = \frac{x_1+x_0}{2}$，实现尺度匹配。

1D Blob检测总结：

用多尺度归一化高斯二阶导数 $L(x,\sigma) = f(x) * \sigma^2 G_\sigma’‘(x)$ 滤波
Blob通过 $L(x,\sigma)$ 的极值检测：$(\hat{x}, \hat{\sigma}) = \arg \text{MinMax } L(x,\sigma)$
$\hat{x}$ 和 $\hat{\sigma}$ 分别是位置和特征尺寸

2D Blob检测：拉普拉斯高斯算子

归一化拉普拉斯高斯算子 (NLoG)

2D Blob可通过多尺度归一化拉普拉斯高斯算子检测：

\[\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}\] \[\nabla^2 G(x,y;\sigma) = \left(\frac{x^2+y^2}{\sigma^4} - \frac{2}{\sigma^2}\right) G(x,y;\sigma)\]

归一化拉普拉斯高斯算子： $L(x,y;\sigma) = \sigma^2 \nabla^2 G(x,y;\sigma) * I(x,y)$

尺度选择

给定二值圆和不同尺度的NLoG滤波器，响应随尺度变化。当滤波器尺度与Blob尺度匹配时，响应达到最大。

2D Blob检测步骤：

用不同尺度的NLoG滤波图像
寻找 $L(x,y;\sigma)$ 的极值：$(\hat{x}, \hat{y}, \hat{\sigma}) = \arg \text{MinMax } L(x,y;\sigma)$
$(\hat{x}, \hat{y})$ 是位置，$\hat{\sigma}$ 是特征尺寸

高斯差分算子 (DoG)

DoG作为NLoG的快速近似：

\[G(x,y,k\sigma) - G(x,y,\sigma) \approx (k-1)\sigma^2 \nabla^2 G\]

其中 $k$ 是尺度因子（通常 $k = \sqrt{2}$）。

高斯金字塔的高效构建

利用卷积的结合律：$[f_1(t) * f_2(t)] * f_3(t) = f_1(t) * [f_2(t) * f_3(t)]$

对于高斯函数：$\sigma_Z = \sqrt{\sigma_X^2 + \sigma_Y^2}$

这允许通过已有的高斯滤波结果计算更大尺度的滤波，提高计算效率。

金字塔结构：

第一个八度：${\sigma, \sqrt{2}\sigma, 2\sigma, 2\sqrt{2}\sigma, 4\sigma}$
DoG: ${\sqrt{2}\sigma, 2\sigma, 2\sqrt{2}\sigma, 4\sigma}$
第二个八度（下采样）：${2\sigma, 2\sqrt{2}\sigma, 4\sigma, 4\sqrt{2}\sigma, 8\sigma}$
DoG: ${2\sqrt{2}\sigma, 4\sigma, 4\sqrt{2}\sigma, 8\sigma}$

3D极值检测

在DoG图像中，通过比较像素与其在当前和相邻尺度的3×3×3邻域内的26个邻居来检测极值。

SIFT特征 (Scale-Invariant Feature Transform)

SIFT概述

SIFT特征是”尺度不变关键点的独特图像特征”，基于Blob检测构建具有以下特性的特征描述子：

尺度不变性：通过多尺度检测
旋转不变性：通过主方向对齐
光照鲁棒性：通过归一化梯度直方图
高判别性：128维特征向量

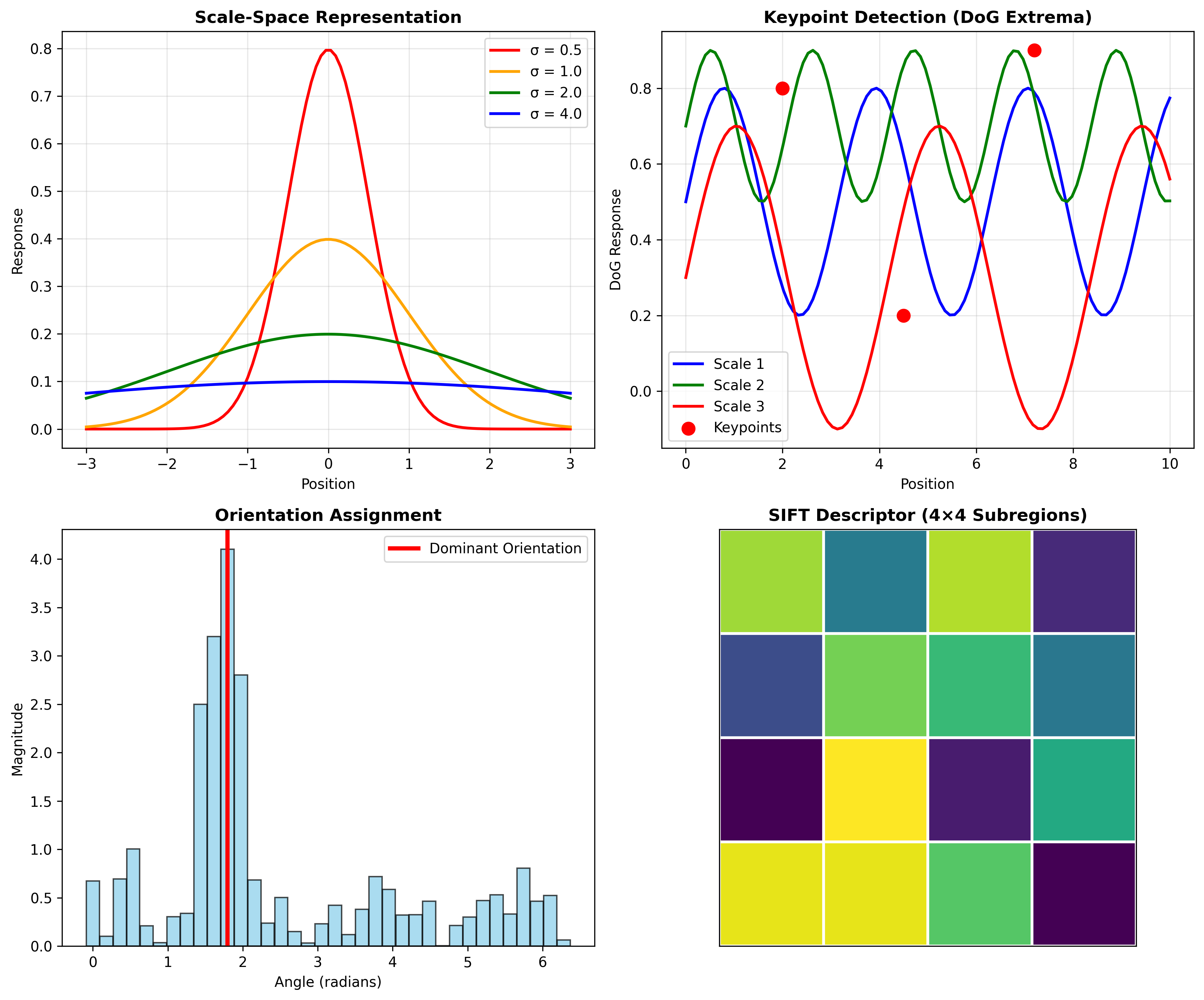
Blob作为尺度不变关键点

Blob通过多尺度NLoG极值检测
缩放后的Blob仍能在适当的尺度层被检测到
尺度归一化后实现尺度不变性
对旋转、遮挡、杂乱和噪声具有鲁棒性

关键点筛选

初始关键点筛选过程：

原始图像：832个DoG极值点
对比度阈值：应用最小对比度阈值后剩余729个
边缘响应过滤：消除强边缘响应后剩余536个

边缘响应过滤原理： 使用Hessian矩阵的主曲率比： $\mathbf{H} = \begin{bmatrix} D_{xx} & D_{xy} \\ D_{xy} & D_{yy} \end{bmatrix}$

\[\frac{\text{Tr}(\mathbf{H})^2}{\text{Det}(\mathbf{H})} = \frac{(\alpha + \beta)^2}{\alpha\beta} = \frac{(r\beta + \beta)^2}{r\beta^2} = \frac{(r+1)^2}{r}\]

其中 $\alpha$ 和 $\beta$ 是Hessian矩阵的特征值，$r = \alpha/\beta$。

主方向计算

计算关键点的主方向：

使用关键点尺度 $\sigma$ 选择平滑图像 $L(x,y;\sigma)$
在关键点周围计算梯度幅值和方向：
- $m(x,y) = \sqrt{L_x^2 + L_y^2}$
- $\theta(x,y) = \tan^{-1}(L_y/L_x)$
构建方向直方图（36个方向bin）
直方图的峰值定义主方向

旋转不变性

使用主方向消除旋转：所有后续计算都相对于主方向进行，实现旋转不变性。

SIFT描述符计算

梯度直方图作为描述符：

在关键点周围的16×16窗口内计算梯度
将窗口划分为4×4子区域
每个子区域计算8方向的梯度直方图
生成128维特征向量（4×4×8=128）

重要实现细节：

使用关键点尺度选择高斯模糊级别
预计算所有金字塔层的梯度以提高效率
使用高斯窗口避免突变
归一化特征向量以减少光照影响

SIFT特征匹配

描述符比较方法：

L2距离： $d(H_1, H_2) = \sqrt{\sum_k (H_1(k) - H_2(k))^2}$
归一化相关性： $d(H_1, H_2) = \frac{\sum_k[(H_1(k) - \bar{H_1})(H_2(k) - \bar{H_2})]}{\sqrt{\sum_k(H_1(k) - \bar{H_1})^2} \sqrt{\sum_k(H_2(k) - \bar{H_2})^2}}$
直方图交集： $d(H_1, H_2) = \sum_k \min(H_1(k), H_2(k))$

SIFT特性总结

Blob检测 → 尺度不变
主方向对齐 → 旋转不变
归一化梯度直方图 → 独特性、光照鲁棒性
图像金字塔 → 计算高效
用于图像匹配和识别

HoG特征 (Histogram of Oriented Gradients)

HoG特征概述

HoG特征用于描述局部对象外观和形状，通过梯度分布进行特征化，无需精确的梯度位置信息。

HoG计算步骤：

图像预处理：调整图像尺寸至128×64
梯度计算：计算每个像素的梯度幅值和方向
细胞划分：将图像分为8×8像素的细胞，计算9方向直方图
块归一化：将2×2细胞组成块，步长为1进行滑动
特征归一化：对直方图进行归一化，增强对光照和阴影的鲁棒性

HoG vs SIFT

计算方式差异：

HoG：密集网格、单一尺度、无主方向对齐
SIFT：稀疏关键点、多尺度、主方向对齐

应用差异：

SIFT：优化用于稀疏宽基线匹配
HoG：用于密集的空间形状鲁棒编码

HoG在目标检测中的应用

检测流程：

提取HoG特征
训练线性分类器（如SVM）
用滑动窗口在不同尺度下运行分类器

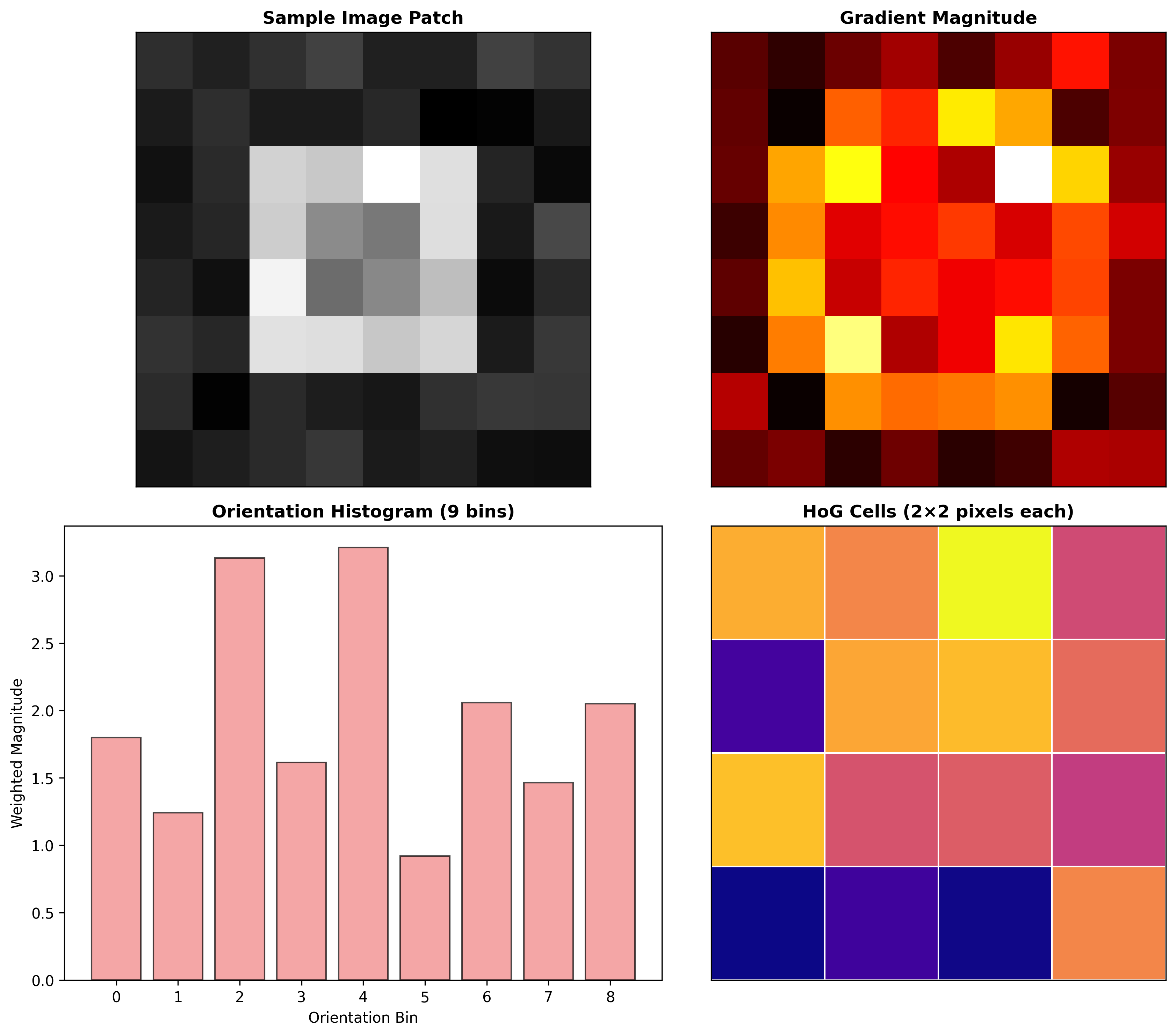
应用与扩展

ControlNet中的应用

Canny边缘检测在现代深度学习中仍有重要应用，如ControlNet中用于控制文本到图像的扩散模型生成。

仍未解决的问题

尽管有这些先进的方法，边缘检测在复杂场景中仍是一个未完全解决的问题，特别是在区分语义边缘和纹理边缘方面。

总结

特征检测是计算机视觉的基础任务：

边缘检测： 识别图像中的强度不连续，Canny算法是经典方法
角点检测： 定位可靠的特征点，Harris检测器基于二阶矩矩阵
Blob检测： 识别感兴趣区域，为SIFT等高级特征的前身

这些方法为图像匹配、目标检测和3D重建等高级视觉任务提供了基础。