AI数学基础 - 第3-4讲: 随机变量

1. 随机变量的基本概念

1.1 随机变量的定义

直观描述

某变量 $X$ 随机取值，则 $X$ 是随机变量。

严格描述

对于样本空间 $\Omega = {\omega}$，$X = X(\omega)$ 是在 $\Omega$ 上有定义的实值函数，而且对任何实数 $c$，事件 ${\omega : X(\omega) \leq c}$ 是有概率的（属于事件域），将 $X$ 称为随机变量。

1.2 经典例子

例 1.2 盒中有 5 个球，其中有 2 个白球，3 个黑球。从中任取 3 个球，将其中所含的白球的数目记为 $X$。

建模：将球编号，1∼3 表示黑球，4,5 表示白球
样本空间：$\omega = (i, j, k)$，其中 $1 \leq i < j < k \leq 5$，$ \Omega = C_5^3 = 10$
概率计算：
- 满足 $X = 0$ 的 $\omega$ 有 $C_2^0 C_3^3 = 1$ 个
- 满足 $X = 1$ 的 $\omega$ 有 $C_2^1 C_3^2 = 6$ 个
- 满足 $X = 2$ 的 $\omega$ 有 $C_2^2 C_3^1 = 3$ 个

因此：$P(X = 1) = \frac{6}{10}$，$P(X \leq 1) = \frac{7}{10}$

例 1.6 某公共汽车站每隔 10 分钟会有一辆某路公交车到达。某乘客随机在任意时刻到达车站。

候车时间 $X$（单位：分钟）为随机变量，$0 \leq X \leq 10$。

利用几何概型： $P(X \leq 3) = \frac{3}{10}, \quad P(2 \leq X \leq 6) = \frac{4}{10}$

2. 离散随机变量

2.1 离散随机变量的定义

定义 2.1 $X$ 是离散型随机变量指：$X$ 取有限个值 $x_1, \cdots, x_n$，或可列个值 $x_1, x_2, \cdots$。$X$ 的概率分布（列）指：

\[p_k = P(X = x_k), \quad k = 1, \cdots, n \text{ 或 } k = 1, 2, \cdots\]

概率分布表：

$X$	$x_1$	$x_2$	$\cdots$	$x_k$	$\cdots$
$p$	$p_1$	$p_2$	$\cdots$	$p_k$	$\cdots$

性质：

非负性：$p_k \geq 0, \forall k$
规范性：$\sum_{k=1}^n p_k = 1$ 或 $\sum_{k=1}^{\infty} p_k = 1$

2.2 重要的离散分布

2.2.1 两点分布（伯努利分布）

记号：$X \sim B(1, p)$，参数 $0 \leq p \leq 1$

概率函数： $P(X = 1) = p, \quad P(X = 0) = 1 - p$

模型：投币实验，投到正面则 $X = 1$；投到反面则 $X = 0$

示性函数：$1_A$ 表示事件 $A$ 发生则取 1；$A$ 不发生则取 0

例 2.1 100 件产品中有 3 件次品。从中任取一件。 $A =$ “取到合格品”，$X = 1_A$，$p = 0.97$。

2.2.2 二项分布

记号：$X \sim B(n, p)$，参数 $n \geq 1, 0 \leq p \leq 1$

概率函数： $P(X = k) = C_n^k p^k (1-p)^{n-k}, \quad k = 0, 1, \cdots, n$

模型：独立投币 $n$ 次，正面的总次数

定理 2.1（分布列的最大值点）：

若 $(n+1)p \notin \mathbb{Z}$，则 $k_0 = [(n+1)p]$
若 $(n+1)p \in \mathbb{Z}$，则 $k_0 = (n+1)p$ 或 $(n+1)p - 1$

证明思路：利用组合数公式 $\frac{p_n(k+1)}{p_n(k)} = \frac{n-k}{k+1} \cdot \frac{p}{1-p}$

当 $\frac{n-k}{k+1} \cdot \frac{p}{1-p} > 1$ 等价于 $k < (n+1)p - 1$ 时：

$k < (n+1)p - 1$ 时，$p_n(k+1) > p_n(k)$
$k > (n+1)p - 1$ 时，$p_n(k+1) < p_n(k)$
$k = (n+1)p - 1$ 时，$p_n(k+1) = p_n(k)$

2.2.3 泊松分布

记号：$X \sim P(\lambda)$，参数 $\lambda > 0$

概率函数： $P(X = k) = \frac{\lambda^k}{k!} e^{-\lambda}, \quad k = 0, 1, 2, \cdots$

模型：例如研究放射性物质在 8 分钟内放射出的粒子数 $X$

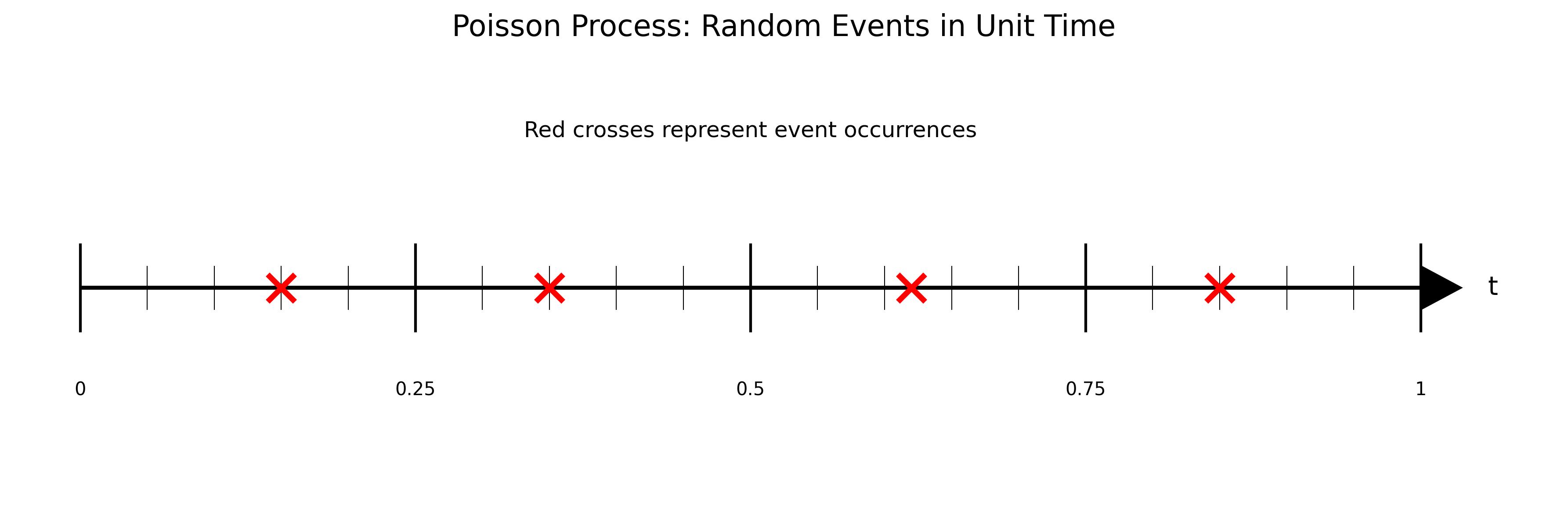
泊松近似：$X$ 近似服从 $B(n, p)$，当 $n$ 很大，$p$ 很小，$np = \lambda$ 适中时： $P(X = k) = C_n^k p^k (1-p)^{n-k} \approx \frac{n!}{k!(n-k)!} p^k (1-p)^n$ $\approx \frac{(np)^k}{k!} \left(1 - \frac{\lambda}{n}\right)^n = \frac{\lambda^k}{k!} e^{-\lambda}$

这就是 §1.7 第一近似公式。

分布列最大值点：$k_0 = [\lambda]$

证明：注意到 $p_{k+1} = \frac{\lambda}{k+1} p_k$，故：

若 $k+1 \leq \lambda$，则 $p_{k+1} \geq p_k$
若 $k+1 \geq \lambda$，则 $p_{k+1} \leq p_k$

因此当 $k_0 = [\lambda]$ 时，分布列取最大值。

重要应用题：已知某商场一天来的顾客服从参数为 $\lambda$ 的泊松分布，而每个来商场的顾客购物概率为 $p$，证明此商场一天内购物的顾客数服从参数为 $\lambda p$ 的泊松分布。

解：用 $Y$ 表示商场内一天购物的顾客数，则由全概率公式知： $P(Y = k) = \sum_{i=k}^{\infty} P(X = i) P(Y = k \mid X = i) = \sum_{i=k}^{\infty} \frac{\lambda^i e^{-\lambda}}{i!} C_i^k p^k (1-p)^{i-k}$ $= \frac{(\lambda p)^k}{k!} e^{-\lambda} \sum_{i=k}^{\infty} \frac{[\lambda(1-p)]^{i-k}}{(i-k)!} = \frac{(\lambda p)^k}{k!} e^{-\lambda} e^{\lambda(1-p)} = \frac{(\lambda p)^k}{k!} e^{-\lambda p}$

2.2.4 超几何分布

记号：$X \sim H(N, D, n)$，参数 $N, D, n$

概率函数： $P(X = k) = \frac{C_D^k C_{N-D}^{n-k}}{C_N^n}, \quad k = 0, 1, \cdots, n$

模型：$N$ 个产品，$D$ 个次品，任取 $n$ 个，抽到的次品数为 $X$

放回抽样 vs 不放回抽样：二项分布 vs 超几何分布

定理 2.3（超几何分布的二项逼近）：给定 $n$，当 $N \to \infty$，$\frac{D}{N} \to p$ 时， $\frac{C_D^k C_{N-D}^{n-k}}{C_N^n} \to C_n^k p^k (1-p)^{n-k}, \quad k \geq 0$

直观解释：当总量 $N$ 很大，次品占比为 $p$ 时，从整批产品随机抽取 $n$ 个，抽到次品的个数 $k$ 近似服从参数为 $p, n$ 的二项分布。

证明：由于 $0 < p < 1$，当 $N$ 充分大时，$n < D < N$，且 $n$ 是固定的，易知： $\frac{C_D^k C_{N-D}^{n-k}}{C_N^n} = C_n^k \left(\prod_{i=1}^k \frac{D-i+1}{N}\right) \left(\prod_{i=1}^{n-k} \frac{N-D-i+1}{N}\right) \left(\prod_{i=1}^n \frac{N}{N-i+1}\right)$ $\to C_n^k p^k (1-p)^{n-k} \quad (N \to \infty)$

2.2.5 几何分布

记号：$X \sim G(p)$，参数 $0 < p < 1$

概率函数： $P(X = k) = (1-p)^{k-1} p, \quad k = 1, 2, \cdots$

模型：独立重复投币中，第一次投到正面时的投币次数

重要性质：

$P(X > n) = (1-p)^n, \forall n \geq 0$
无记忆性：$P(X - n = k \mid X > n) = P(X = k)$

无记忆性的唯一性定理：设 $X$ 是只取自然数的离散随机变量，若 $X$ 的分布具有无记忆性，证明 $X$ 的分布一定为几何分布。

证明：由无记忆性知： $P(X > n + m \mid X > m) = \frac{P(X > n + m)}{P(X > m)} = P(X > n)$

将 $n$ 换为 $n-1$ 仍有： $P(X > n + m - 1) = P(X > n - 1) P(X > m)$

两式相减有： $P(X = n + m) = P(X = n) P(X > m)$

设 $P(X = 1) = p$，若取 $n = m = 1$ 有： $P(X = 2) = p(1-p)$

若取 $n = 2, m = 1$ 则有： $P(X = 3) = P(X = 2) P(X > 1) = p(1-p)^2$

若令 $P(X = k) = p(1-p)^{k-1}$，则用数学归纳法得： $P(X = k+1) = P(X = k) P(X > 1) = p(1-p)^k, \quad k = 0, 1, \cdots$

这表明 $X$ 的分布为几何分布。

2.2.6 离散均匀分布

概率函数： $P(X = k) = \frac{1}{N}, \quad k = 1, \cdots, N$

模型：古典概型

3. 连续随机变量

3.1 连续随机变量的定义

定义 3.1 连续型随机变量指：存在 $p(x)$ 使得 $P(a \leq X \leq b) = \int_a^b p(x) dx, \quad \forall a < b$

称 $p(\cdot)$ 为 $X$ 的概率密度（函数），也记为 $p_X(\cdot)$。

性质：

非负性：$p(x) \geq 0$
规范性：$\int_{-\infty}^{\infty} p(x) dx = 1$
$P(X = x) = 0$（在任意一点选中的概率都为 0）
若 $p(\cdot)$ 在 $x$ 连续，则 $P(X \in [x, x + \Delta x]) = p(x)\Delta x + o(\Delta x)$
单独谈论一个点 $x$ 对应的 $p(x)$ 没有意义

3.2 重要的连续分布

3.2.1 均匀分布

记号：$X \sim U(a, b)$，参数 $a < b$

概率密度函数：

\[p(x) = \begin{cases} \frac{1}{b-a}, & \text{若 } a \leq x \leq b \\ 0, & \text{否则} \end{cases}\]

也可写作：$p(x) = \frac{1}{b-a} \mathbf{1}_{{a \leq x \leq b}}$

注意：$a \leq x \leq b$ 可改为 $a < x < b$, $a < x \leq b$, $a \leq x < b$

模型：某公共汽车站每隔 10 分钟会有一班公交车到达，一位搭乘该车的乘客在任意时刻到达车站是等可能的，则他的候车时间 $X$ 满足 $[0, 10]$ 上的均匀分布。

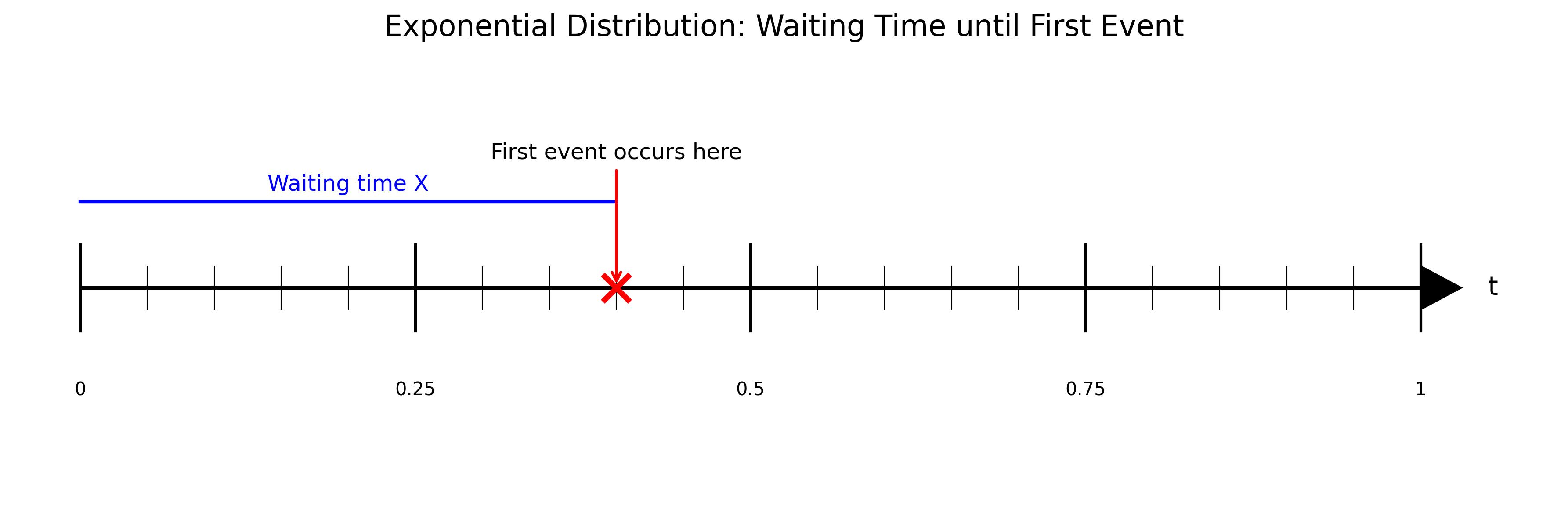
3.2.2 指数分布

记号：$X \sim \text{Exp}(\lambda)$，参数 $\lambda > 0$

概率密度函数： $p(x) = \lambda e^{-\lambda x}, \quad x > 0$

模型：例如，第一个粒子的放射时刻、等待时间、寿命

重要性质：

若 $X$ 服从参数为 $\lambda$ 的指数分布，则对任何 $0 \leq a < b$ 有： $P(a < X < b) = \lambda \int_a^b e^{-\lambda x} dx = e^{-\lambda a} - e^{-\lambda b}$
$P(X > a) = e^{-\lambda a}$

定理 3.1（无记忆性）： $P(X - s > t \mid X > s) = e^{-\lambda t}, \quad \forall t, s \geq 0$

证明： $P(X - s > t \mid X > s) = \frac{P(X > s + t)}{P(X > s)} = \frac{e^{-\lambda(s+t)}}{e^{-\lambda s}} = e^{-\lambda t} = P(X > t)$

3.2.3 正态分布

记号：$X \sim N(\mu, \sigma^2)$，参数 $\mu \in \mathbb{R}, \sigma > 0$

概率密度函数： $p(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left\{-\frac{(x-\mu)^2}{2\sigma^2}\right\}$

标准正态分布：$N(0, 1)$ $\phi(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}$

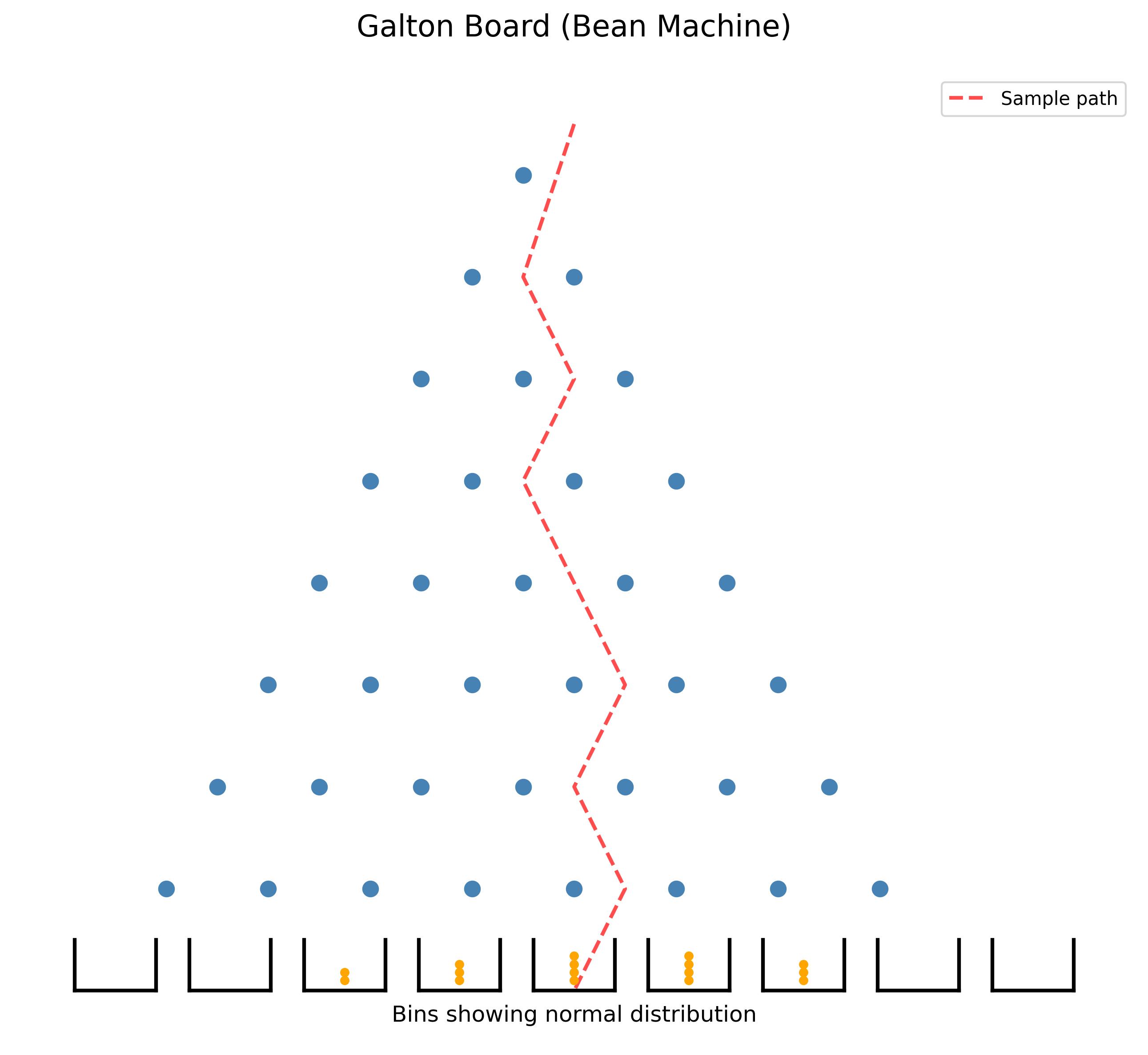
标准正态分布积分的计算：利用极坐标变换证明 $\int_{-\infty}^{\infty} \phi(x) dx = 1$：

\[\left(\int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} dx\right)^2 = \frac{1}{2\pi} \iint_{\mathbb{R}^2} e^{-\frac{x^2+y^2}{2}} dx dy\]

做极坐标变换：$x = r\cos\theta, y = r\sin\theta$，雅可比行列式 $\begin{vmatrix} \frac{\partial x}{\partial r} & \frac{\partial y}{\partial r} \ \frac{\partial x}{\partial \theta} & \frac{\partial y}{\partial \theta} \end{vmatrix} = r$

因此： $= \frac{1}{2\pi} \int_0^{2\pi} \left(\int_0^{\infty} e^{-\frac{r^2}{2}} r dr\right) d\theta = \int_0^{\infty} e^{-R} dR = 1$

对一般正态分布，令 $y = \frac{x-\mu}{\sigma}$，则： $\int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi} \cdot \sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} dx = \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}} e^{-\frac{y^2}{2}} dy = 1$

标准正态分布函数： $\Phi(x) = \int_{-\infty}^x \phi(t) dt$

性质：$\Phi(-x) = 1 - \Phi(x)$

定理 3.2：令 $x^* = \frac{x-\mu}{\sigma}$，则 $P(a < X < b) = \int_a^b \frac{1}{\sigma} \phi\left(\frac{x-\mu}{\sigma}\right) dx = \Phi(b^*) - \Phi(a^*)$

推论 3.1：查表得 $\Phi(3) = 0.9987$，因此 $P(\mu - 3\sigma < X < \mu + 3\sigma) = \Phi(3) - \Phi(-3) = 0.9974$

这就是著名的3σ原则。

3.2.4 伽马分布

记号：$X \sim \Gamma(\alpha, \beta)$，参数 $\alpha, \beta > 0$

概率密度函数： $p(x) = \frac{\beta^{\alpha}}{\Gamma(\alpha)} x^{\alpha-1} e^{-\beta x}, \quad x > 0$

其中 $\Gamma(\alpha) = \int_0^{\infty} y^{\alpha-1} e^{-y} dy$

伽马函数的重要性质： $\Gamma(\alpha + 1) = \alpha \Gamma(\alpha)$

证明： $\int_0^{\infty} y^{\alpha} e^{-y} dy = \left[-y^{\alpha} e^{-y}\right]_0^{\infty} + \int_0^{\infty} \alpha y^{\alpha-1} e^{-y} dy = \alpha \Gamma(\alpha)$

特殊值：

$\Gamma(1) = 1$
$\Gamma\left(\frac{1}{2}\right) = \sqrt{\pi}$

\[\Gamma\left(\frac{1}{2}\right) = \int_0^{\infty} \frac{1}{\sqrt{y}} e^{-y} dy = \sqrt{2} \int_0^{\infty} e^{-\frac{x^2}{2}} dx = \sqrt{\pi}\]

与指数分布的关系：当 $\alpha = 1$ 时就是指数分布 $\text{Exp}(\beta)$

小结

本讲介绍了随机变量的基本概念和重要分布：

离散分布总结

分布	记号	概率函数	模型	重要性质
伯努利	$B(1,p)$	$P(X=1)=p$	投币一次	示性函数
二项	$B(n,p)$	$C_n^k p^k (1-p)^{n-k}$	投币$n$次	最大值点
泊松	$P(\lambda)$	$\frac{\lambda^k}{k!}e^{-\lambda}$	放射性粒子数	二项近似
超几何	$H(N,D,n)$	$\frac{C_D^k C_{N-D}^{n-k}}{C_N^n}$	不放回抽样	二项逼近
几何	$G(p)$	$(1-p)^{k-1}p$	首次成功时间	无记忆性
离散均匀	-	$\frac{1}{N}$	古典概型	-

连续分布总结

分布	记号	密度函数	模型	重要性质
均匀	$U(a,b)$	$\frac{1}{b-a}$	候车时间	几何概型
指数	$\text{Exp}(\lambda)$	$\lambda e^{-\lambda x}$	等待时间	无记忆性
正态	$N(\mu,\sigma^2)$	$\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$	测量误差	3σ原则
伽马	$\Gamma(\alpha,\beta)$	$\frac{\beta^{\alpha}}{\Gamma(\alpha)} x^{\alpha-1} e^{-\beta x}$	等待时间推广	包含指数分布

重要概念

无记忆性：几何分布和指数分布的重要特征
泊松近似：二项分布在 $n$ 大 $p$ 小时的极限情形
标准化：正态分布的重要计算技巧
极限定理：超几何分布到二项分布的逼近