ML - 2: Logistic Regression (逻辑回归)

1. 二分类问题设定

问题定义

输入: $X \in \mathbb{R}^d$
输出: $y \in {0, 1}$ （负类/正类）
使用线性模型: $f(x) = w^T x + b \in \mathbb{R}$

核心问题

$f(x) \in \mathbb{R}$，但 $y \in {0, 1}$ —— 值域不匹配
需要软预测 (soft prediction)：预测概率 $P(y=1 \mid x)$ —— How likely?

解决方案

我们需要使用 $f(x) = w^T x + b$ 来拟合 $P(y=1 \mid x=x_i)$

使用 Sigmoid 函数: $\sigma(z) = \frac{1}{1 + e^{-z}}$，将 $\mathbb{R} \rightarrow [0, 1]$

2. Sigmoid函数

定义与性质

\[\sigma(z) = \frac{1}{1 + e^{-z}}\]

定义域: $\mathbb{R}$，值域: $[0, 1]$
单调递增函数
对称性: $1 - \sigma(z) = \sigma(-z)$

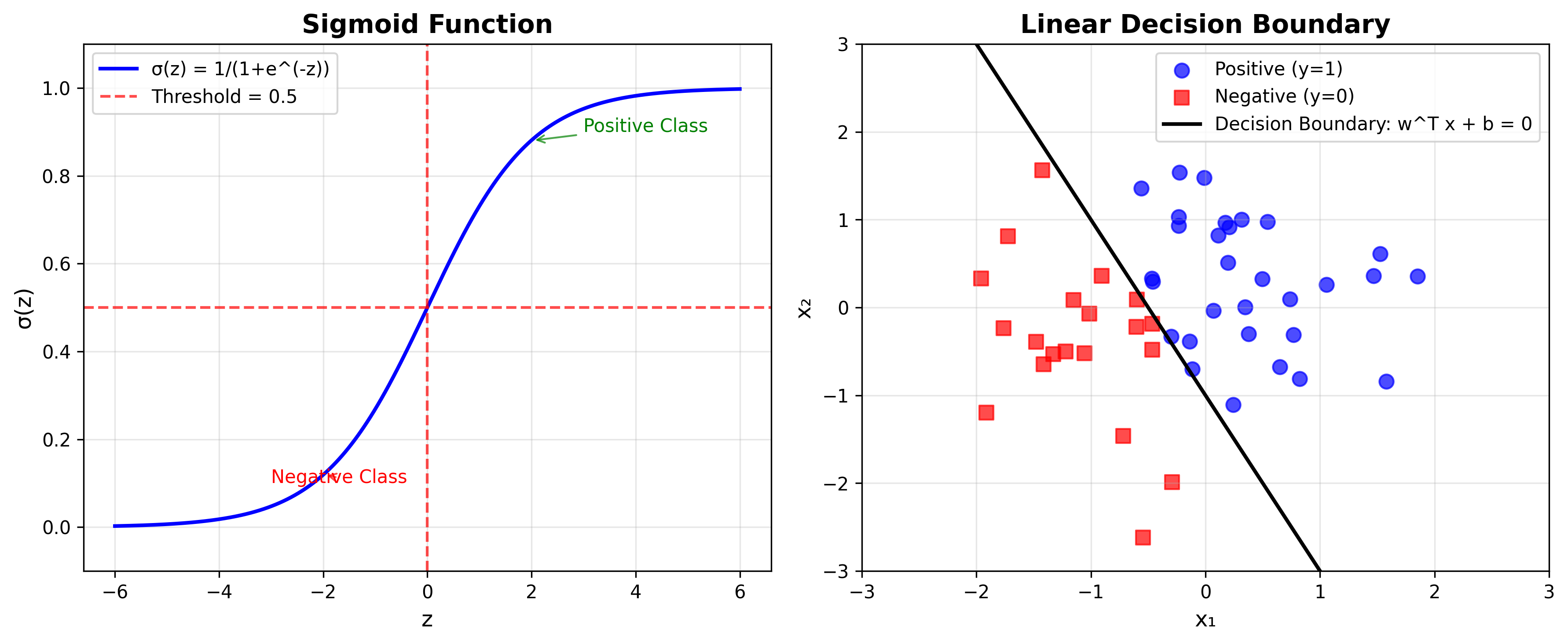
决策边界

设置阈值 $\sigma(z) = 0.5$ 来输出硬预测：

当 $w^T x + b > 0$ 时，预测为正类
当 $w^T x + b < 0$ 时，预测为负类
分离超平面: $w^T x + b = 0$

3. 最大似然估计 (MLE)

如何找到参数 $w$ 和 $b$？

使用最大似然估计，找到参数 $w, b$ 使得在整个训练数据上的似然 $P(y=y_i \mid x=x_i)$ 最大化。

似然函数

对于单个样本，条件概率为：

\[P(y_i \mid x_i) = \begin{cases} \sigma(w^T x_i + b) & \text{if } y_i = 1 \\ 1 - \sigma(w^T x_i + b) & \text{if } y_i = 0 \end{cases}\]

统一表示: $P(y_i \mid x_i) = \sigma(w^T x_i + b)^{y_i} [1 - \sigma(w^T x_i + b)]^{1-y_i}$

整体似然: $\mathcal{L} = \prod_{i \in [n]} P(y_i \mid x_i; w, b)$

最大化对数似然

\[\log \mathcal{L} = \sum_{i \in [n]} [y_i \log(\sigma(w^T x_i + b)) + (1-y_i) \log(1-\sigma(w^T x_i + b))]\]

等价于最小化: $\min_{w,b} \sum_{i \in [n]} [-y_i \log(\sigma(w^T x_i + b)) - (1-y_i) \log(1-\sigma(w^T x_i + b))]$

这就是交叉熵损失函数 (Cross Entropy Loss)。

4. 交叉熵损失函数

信息论基础

熵 (Entropy)

对于概率分布 $P(y)$： $H(P) = \sum_y P(y) \log \frac{1}{P(y)} = -\sum_y P(y) \log P(y)$

熵衡量了系统的不确定性。

交叉熵 (Cross Entropy)

交叉熵涉及两个分布 $P$ 与 $Q$。其中 $P$ 为实际分布，$Q$ 为模型预测的分布。其度量的是用分布 $Q$ 编码分布 $P$ 所需的平均信息量：

\[H(P, Q) = -\sum_y P(y) \log Q(y)\]

KL散度

\[KL(P||Q) = \sum_y P(y) \log \frac{P(y)}{Q(y)} \geq 0\] \[= -\sum_y P(y) \log Q(y) - (-\sum_y P(y) \log P(y)) = H(P, Q) - H(P)\]

5. 寻找闭式解

参数重写

定义增广矩阵形式：

$\hat{X} = \begin{bmatrix} X \ \mathbf{1}^T \end{bmatrix} \in \mathbb{R}^{(d+1) \times n}$
$\hat{w} = \begin{bmatrix} w \ b \end{bmatrix} \in \mathbb{R}^{d+1}$

则 $f(x) = w^T x + b = \hat{w}^T \hat{x}$

损失函数

\[L(\hat{w}) = -\sum_{i \in [n]} [y_i \log \sigma(\hat{w}^T \hat{x}_i) + (1-y_i) \log(1-\sigma(\hat{w}^T \hat{x}_i))]\] \[= -\sum_{i \in [n]} [y_i \hat{w}^T \hat{x}_i - \log(1 + e^{\hat{w}^T \hat{x}_i})]\]

梯度计算

\[\frac{\partial L(\hat{w})}{\partial \hat{w}} = -\sum_{i \in [n]} \left[y_i - \frac{e^{\hat{w}^T \hat{x}_i}}{1 + e^{\hat{w}^T \hat{x}_i}}\right] \hat{x}_i\] \[= -\sum_{i \in [n]} [y_i - \sigma(\hat{w}^T \hat{x}_i)] \hat{x}_i\] \[= -\sum_{i \in [n]} [y_i - P(y=1 \mid x_i)] \hat{x}_i\]

梯度下降

\[\hat{w} \leftarrow \hat{w} + \alpha \sum_{i \in [n]} [y_i - P(y=1 \mid x_i)] \hat{x}_i\]

收敛条件

当 $\frac{\partial L(\hat{w})}{\partial \hat{w}} = 0$ 时，即存在 $P(y=1 \mid x_i) = y_i$，称为线性可分。

6. 线性可分情况的讨论

在线性可分情况下，存在非常多的分割超平面：

大部分问题并非线性可分
线性可分时，加入 L2 正则化便可找到唯一解： $\min_{\hat{w}} L(\hat{w}) + \frac{\lambda}{2} ||\hat{w}||^2$

7. 为什么不能使用平方损失函数？

$y_i \in {0, 1}$ 无数值意义
受离群值影响严重
缺乏概率解释

8. 多分类情况：Softmax回归

问题设定

$y \in {1, 2, …, K}$ —— $K$ 分类问题

K个分类器

\[f_k(x) = w_k^T x + b_k, \quad k \in [K]\]

Softmax函数

\[P(y=k \mid x) = \frac{\exp(w_k^T x + b_k)}{\sum_{j=1}^K \exp(w_j^T x + b_j)} \in [0, 1]\]

性质

$\sum_{j \in [K]} P(y=j \mid x) = 1$ （归一化的概率）
当 $f_k(x) » f_j(x)$ 时，$P(y=k \mid x) \approx 1$

MLE目标

\[\max \sum_{i \in [n]} \log \frac{\exp(w_{y_i}^T x_i + b_{y_i})}{\sum_{j \in [K]} \exp(w_j^T x_i + b_j)}\]

注意: 当 $K=2$ 时，softmax回归等价于逻辑回归。

9. 对于线性回归，可否由MLE导出损失？

高斯分布

$x \sim \mathcal{N}(\mu, \sigma^2)$，其中 $\mu$ 为均值，$\sigma^2$ 为方差

\[P(x) = \mathcal{N}(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\]

在 $2\sigma$ 之内占 $95\%$

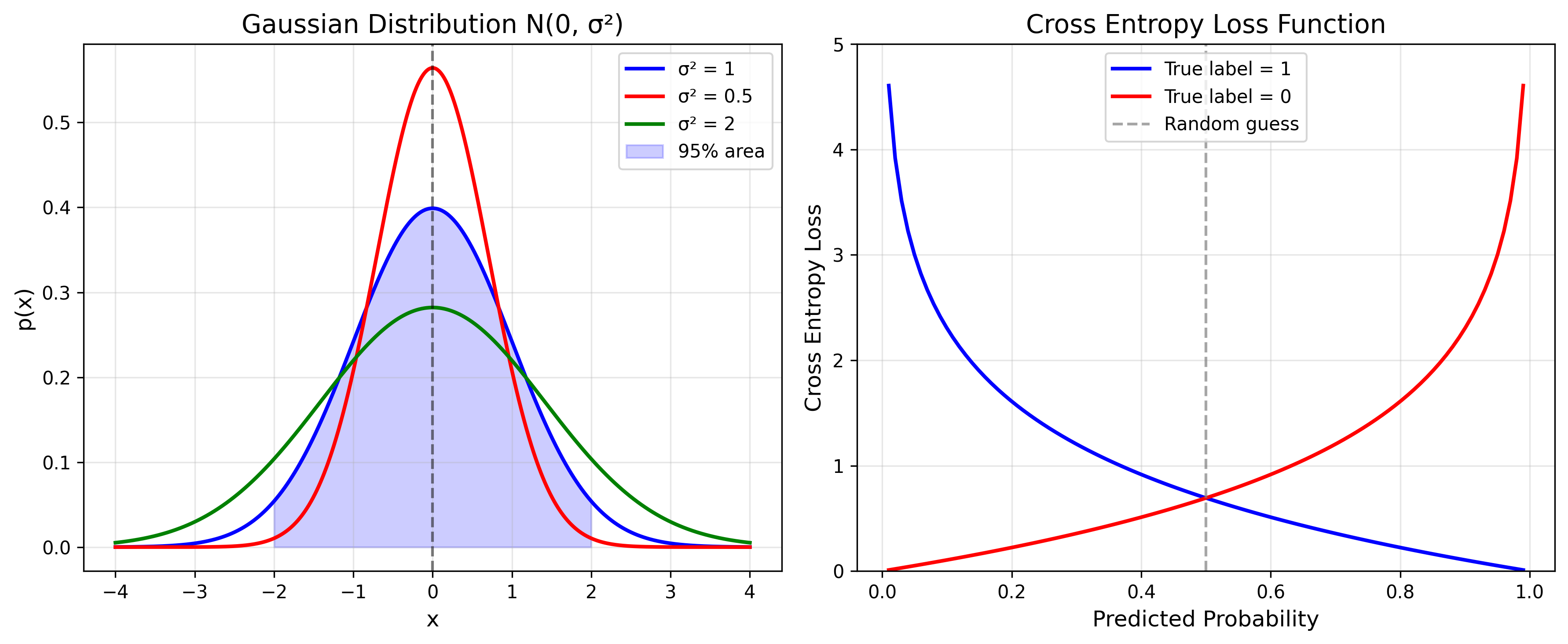
噪声模型

$y = w^T x + b + \epsilon$ 其中 $\epsilon$ 服从高斯分布：$\epsilon \sim \mathcal{N}(0, \sigma^2)$

此时对 $y$ 进行概率建模： $P(y \mid x; w, b, \sigma^2) = \mathcal{N}(w^T x + b, \sigma^2)$

Log-likelihood

\[\max \sum_{i \in [n]} \log \mathcal{N}(y_i|w^T x_i + b, \sigma^2)\] \[= \max \sum_{i \in [n]} \left[\log\left(\frac{1}{\sqrt{2\pi\sigma^2}}\right) - \frac{1}{2\sigma^2}(y_i - (w^T x_i + b))^2\right]\] \[= \min \frac{1}{2\sigma^2} \sum_{i \in [n]} (y_i - (w^T x_i + b))^2\]

结论：推出了平方损失的等价形式！

10. 最大后验估计 (MAP)

先验分布

\[P(\hat{w}) = \mathcal{N}(\hat{w}|0, \sigma_w^2 I)\]

$\hat{w}$ 也是随机变量

后验分布

\[P(\hat{w} \mid y, X) = \frac{P(y \mid X, \hat{w}) P(\hat{w})}{P(y \mid X)} \propto P(y \mid X, \hat{w}) P(\hat{w})\]

MAP目标

\[\max P(\hat{w} \mid y, X) = \max P(y \mid X, \hat{w}) P(\hat{w})\] \[\propto \max \left[\exp\left(-\frac{\sum_{i \in [n]}(y_i - \hat{w}^T \hat{x}_i)^2}{2\sigma^2}\right) \exp\left(-\frac{\hat{w}^T\hat{w}}{2\sigma_w^2}\right)\right]\]

取负log，去掉无关项： $\min \sum_{i \in [n]} (y_i - \hat{w}^T \hat{x}_i)^2 + \frac{\sigma^2}{\sigma_w^2} ||\hat{w}||^2$

结论：岭回归！！

总结

逻辑回归将二分类问题转化为概率建模问题：

使用 Sigmoid 函数将线性输出映射到概率空间
通过最大似然估计学习参数，等价于最小化交叉熵损失
梯度下降求解，线性可分时需要正则化
自然扩展到多分类（Softmax）
从概率视角统一了线性回归（高斯分布）和逻辑回归（伯努利分布）
MAP 估计引出正则化的必要性