ML - 1: Linear Regression (线性回归)

线性回归 (Linear Regression)

• $D = {(x_i,y_i)}$ 为训练集，其中 $x_i \in \mathbb{R}^d,y\in \mathbb{R}$；
• 线性模型：$f(x) = w^Tx + b$，其中 $w\in \mathbb{R}^d,b \in R$，分别称为权重（weight）和偏置（bias）。 $w$ 本质上是在对 $x$ 的每一维进行加权求和。

我们根据什么来决定 $w,b$ 的值呢？我们使用到ERM（经验风险最小化）原则：使用损失函数来进行衡量，并使损失函数最小化。

我们会使用平方损失函数（squared loss function）：

\[L(f(x_i),y_i) = (f(x_i)-y_i)^2 = (w^Tx_i + b - y_i)^2\]

于是经验风险（empirical risk）为：

\[L(f) = \frac{1}{n}\sum_{i=1}^n (w^Tx_i + b - y_i)^2\]

我们要做的就是最小化经验风险：

\[\min_{w,b} L(f) = \min_{w,b} \frac{1}{n}\sum_{i=1}^n (w^Tx_i + b - y_i)^2\]

为了找到最佳的 $w,b$，我们会使用梯度下降法。

梯度下降法 (Gradient Descent)

为了使这个表达式达到最小值，我们对其求梯度（gradient）：

\[\begin{aligned} \frac{\partial L(w,b)}{\partial w} &= -\sum_{i \in [n]}2(y_i - w^Tx_i - b)\cdot \frac{\partial (w^Tx_i)}{\partial w} \\ &= -\sum_{i \in [n]}2x_i(y_i - w^Tx_i - b) \\ \frac{\partial L(w,b)}{\partial b} &= -\sum_{i \in [n]}2(y_i - w^Tx_i - b) \end{aligned}\]

常见矩阵/向量运算的求导

常见的公式：

• $\displaystyle \frac{\partial x^Tx}{\partial x} = 2x$
• $\displaystyle \frac{\partial x^TAx}{\partial x} = (A + A^T)x$
• $\displaystyle \frac{\partial a^Tx}{\partial x} = a$

更多可以查阅 Matrix Cookbook。

实际上，对于任意的矩阵求导，我们只需要对其在每一个维度上进行讨论即可，比如推导：

\[\frac{\partial a^Tx}{\partial x} = \begin{pmatrix} \frac{\partial a^Tx}{\partial x_1} \\ \frac{\partial a^Tx}{\partial x_2} \\ \vdots \\ \frac{\partial a^Tx}{\partial x_d} \end{pmatrix} = \begin{pmatrix} \frac{\partial (a_1x_1 + a_2x_2 + \cdots + a_dx_d)}{\partial x_1} \\ \vdots \\ \frac{\partial (a_1x_1 + a_2x_2 + \cdots + a_dx_d)}{\partial x_d} \end{pmatrix} = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_d \end{pmatrix} = a\]

有了梯度，我们就可以使用梯度下降法来更新 $w,b$ 了：

\[\begin{aligned} w &\leftarrow w - \alpha \frac{\partial L(w,b)}{\partial w} \\ b &\leftarrow b - \alpha \frac{\partial L(w,b)}{\partial b} \end{aligned}\]

其中 $\alpha$ 是学习率（learning rate），控制每次更新的步长,是一个大于0的超参数（hyper parameter）。

梯度下降的终止条件：

• 达到最大迭代次数
• 损失函数的变化小于某个阈值 \(\|w' - w\| < \text{threshold}\)

线性回归问题的闭式解讨论

我们做出如下的定义：

\[X = \begin{pmatrix} x_1^T & 1 \\ x_2^T & 1 \\ \vdots & \vdots \\ x_n^T & 1 \end{pmatrix} \in \mathbb{R}^{n \times (d+1)}\] \[y = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix} \in \mathbb{R}^n\] \[\hat{w} = \begin{pmatrix} w \\ b \end{pmatrix} \in \mathbb{R}^{d+1}\]

此时我们可以将平方损失函数的和写为：

\[L(\hat{w}) = (y-X\hat{w})^T(y-X\hat{w}) = \|y - X\hat{w}\|^2\]

我们对 $L(\hat{w})$ 求导：

\[\begin{aligned} \frac{\partial L(\hat{w})}{\partial \hat{w}} &= \frac{\partial (y - X\hat{w})^T(y - X\hat w)}{\partial \hat{w}} \\ &= \frac{\partial (y^Ty - y^TX\hat{w} - \hat{w}^TX^Ty + \hat{w}^TX^TX\hat{w})}{\partial \hat{w}} \\ &= -2X^T y + 2X^TX\hat{w} \\ &= -2X^T(y-X\hat{w}) \end{aligned}\]

我们令其为0，得到：

\[X^TX \hat{w} = X^Ty\]

当 $X^TX$ 为可逆矩阵时，我们可以直接得到唯一的闭式解（closed-form solution）：

\[\hat{w} = (X^TX)^{-1}X^Ty\]

注意：$X^TX$ 不一定总是可逆的，我们来分情况讨论

• 当 $d+1 \gt n $ 时， \(\mathrm{rank}(X^TX) = \mathrm{rank}(X) \leq \min(n, d+1) = n < d+1\) 但 $X^TX \in \mathbb{R}^{(d+1) \times (d+1)}$，$X^TX$ 不是满秩（not full rank）。此时 $X^TX$ 不可逆。
• 当 $d+1 \leq n$ ，且 $X$的列向量线性相关（linearly dependent）时，$X^TX$ 也不是满秩的，不可逆。

当 $X^TX$ 不可逆时，何时有解？

根据线性代数的知识， $X^TX\hat{w} = X^Ty$ 无解当且仅当 $\mathrm{rank}(X^TX) < \mathrm{rank}([X^TX \mid X^Ty])$。

但是这种情况是不可能的，因为 $\mathrm{rank}(X^TX) = \mathrm{rank}(X)$，而 $\mathrm{rank}([X^TX \mid X^Ty]) = \mathrm{rank}([X \mid y])$，且 $\mathrm{rank}(X) = \mathrm{rank}([X \mid y])$（因为都是 $X$ 的线性组合）。

为了解决 $X^TX$ 不可逆的问题，我们可以使用正则化的方法。

L2正则化和岭回归 (Ridge Regression)

我们在损失函数中加入正则化项（regularization term），此时我们的优化目标变为：

\[\min_{\hat{w}} \; L(\hat{w}) + \lambda \|\hat{w}\|_2^2\]

其中 $\lambda > 0$ 是正则化参数（regularization parameter），是一个超参数。

\(\|\hat{w}\|_2^2 = \hat{w}^T\hat{w} = \sum_{i=1}^{d+1} \hat{w}\_i^2\) 这一个正则项惩罚了一些过大的权重。

我们将正则化后的损失函数写为：

\[J(\hat{w}) = L(\hat{w}) + \lambda \|\hat{w}\|_2^2 = (y - X\hat{w})^T(y - X\hat{w}) + \lambda \hat{w}^T\hat{w}\]

我们对 $J(\hat{w})$ 求导:

\[\begin{aligned} \frac{\partial J(\hat{w})}{\partial \hat{w}} &= \frac{\partial L(\hat{w})}{\partial \hat{w}} + \lambda \frac{\partial \|\hat{w}\|_2^2}{\partial \hat{w}} \\ &= -2X^T(y - X\hat{w}) + 2\lambda \hat{w} \end{aligned}\]

令其为0，得到：

\[(X^TX+ \lambda I ) \hat{w} = X^Ty\]

此时，$X^TX + \lambda I$ 一定是可逆的（因为 $\lambda > 0$），所以我们可以得到唯一的闭式解。

讨论为什么 $X^TX + \lambda I$ 一定是可逆的： 设 $A = X^TX$，则 $A$ 是半正定矩阵（positive semi-definite matrix），即对于任意非零向量 $z$，都有 $z^TAz \geq 0$。 设 $B = A + \lambda I$，其中 $\lambda > 0$，则对于任意非零向量 $z$，都有：

\[z^TBz = z^TAz + \lambda z^Tz \geq \lambda z^Tz > 0\]

因为 $z^Tz > 0$（当 $z$ 非零时）。这表明 $B$ 是正定矩阵（positive definite matrix）。 正定矩阵一定是可逆的，因此 $X^TX + \lambda I$ 一定是可逆的。

事实上，加入正则项不但能保证有唯一解，还能防止过拟合（overfitting）。

$X^TX$是实对称矩阵，因此我们可以对其进行特征值分解（eigen decomposition）：

\[X^TX = Q\Lambda Q^T\]

其中 $Q$ 是正交矩阵（orthogonal matrix），$\Lambda$ 是对角矩阵（diagonal matrix），其对角线上的元素为 $X^TX$的特征值（eigenvalues）。因此$(X^TX)^{-1}$可以写为：

\[(X^TX)^{-1} = Q\Lambda^{-1}Q^T = Q \begin{pmatrix} \frac{1}{\lambda_1} & 0 & \cdots & 0 \\ 0 & \frac{1}{\lambda_2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \frac{1}{\lambda_{d+1}} \end{pmatrix}Q^T\]

如果某个特征值 $\lambda_i$ 非常小，那么 $\frac{1}{\lambda_i}$ 会非常大，这会导致 $(X^TX)^{-1}$ 的值变得非常大，从而使得 $\hat{w} = (X^TX)^{-1}X^Ty$ 变得不稳定，容易受到噪声的影响，导致过拟合。

而加入了正则项之后，不但可以防止某个$\lambda$为0导致矩阵没有逆（此时确定出唯一解），还能防止某个$\lambda$非常小导致的过拟合问题。

L1正则化和Lasso回归 (Lasso Regression)

我们也可以使用L1正则化：

\[\min_{\hat{w}} \; L(\hat{w}) + \lambda \|\hat{w}|_1\]

其中 $|\hat{w}|1 = \sum{i=1}^{d+1} \lvert \hat{w}_i \rvert$。 L1正则化的一个重要性质是它倾向于产生稀疏解（sparse solution），即许多权重会被压缩为零。这在特征选择（feature selection）中非常有用，因为它可以帮助我们识别出最重要的特征。

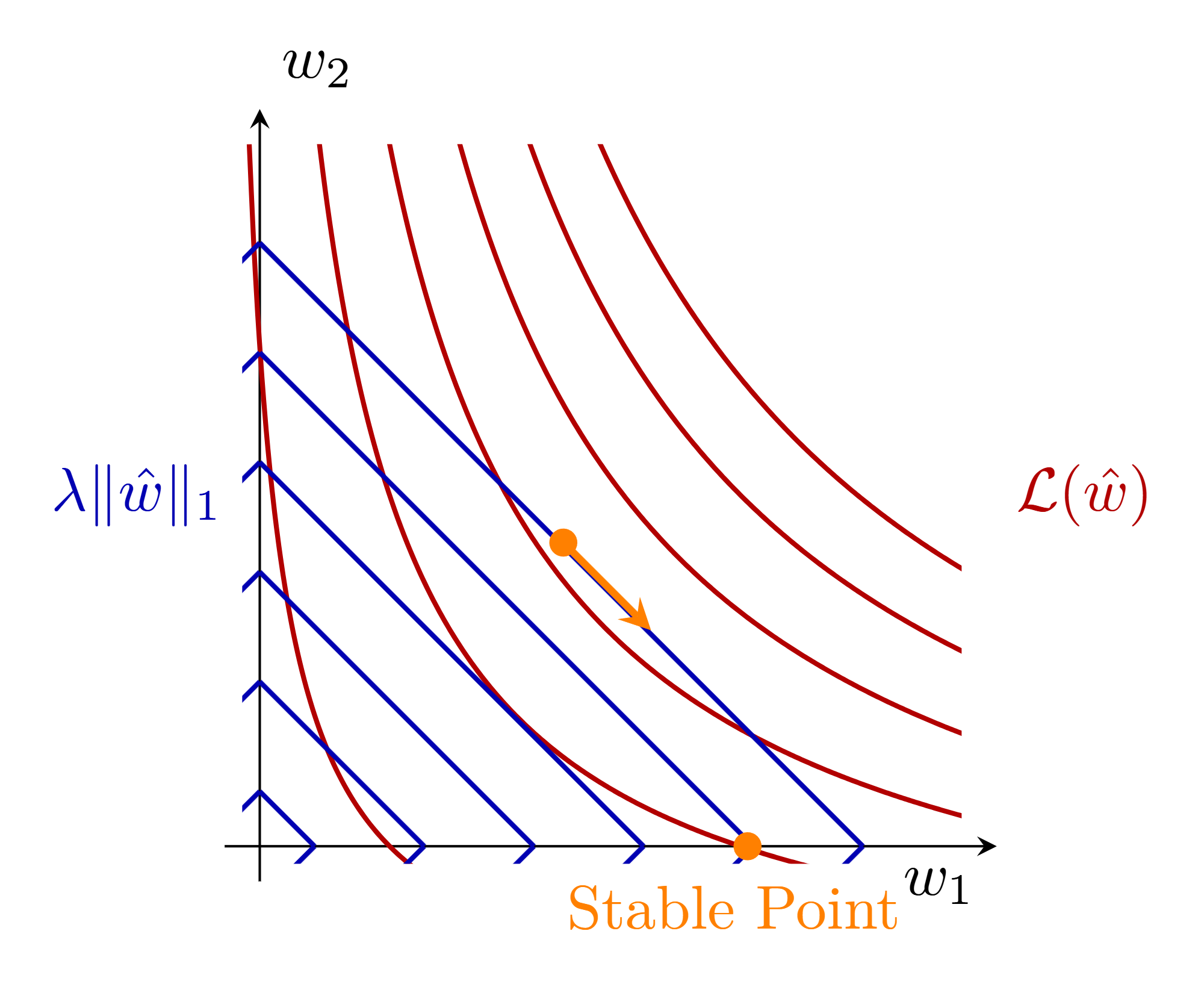
理解L1正则化为什么会产生稀疏解，可以从几何角度来考虑。L1正则化对应的约束区域是一个菱形，而L2正则化对应的约束区域是一个圆。当我们在损失函数的等高线上寻找最优解时，L1正则化更有可能在菱形的顶点处与等高线相切，而这些顶点通常对应于一些权重为零的解。