ICS - 第二讲:位、字节和整数 (Bits, Bytes, and Integers)
第二讲:位、字节和整数 (Bits, Bytes, and Integers)
1. 二进制表示 (Binary Representations)
1.1 为什么使用二进制?
- 最实用的系统:计算机硬件容易实现两种稳定状态
- 电压表示:低电压(0V-0.5V)表示0,高电压(2.8V-3.3V)表示1
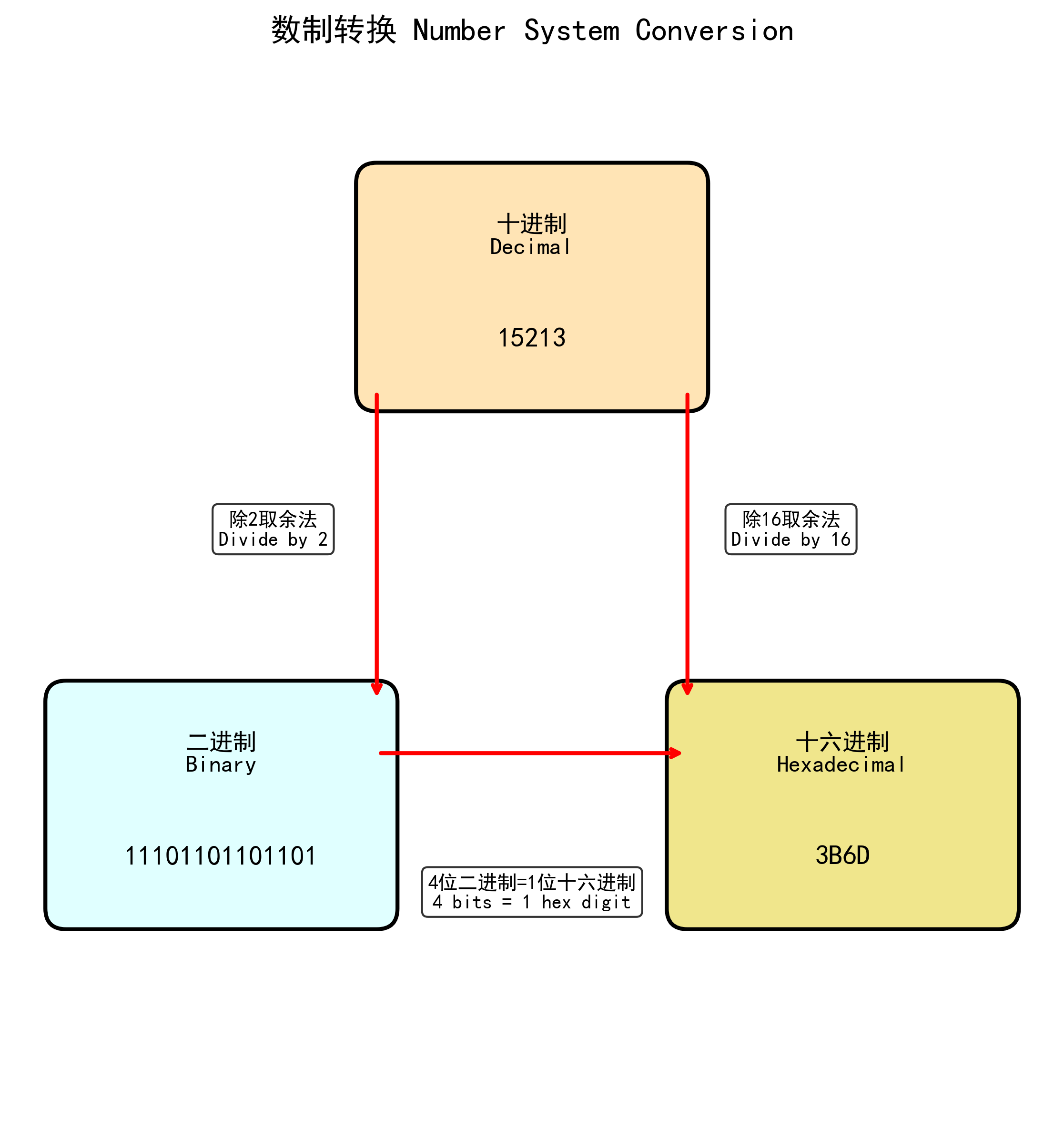
1.2 数制转换
- 十进制转二进制:15213₁₀ = 11101101101101₂
- 十进制转十六进制:15213₁₀ = 3B6D₁₆
- 科学计数法:1.5213 × 10⁴ = 1.11011011011012 × 2¹³
2. 字节编码 (Encoding Byte Values)
2.1 字节 = 8位
- 二进制范围:00000000₂ 到 11111111₂
- 十进制范围:0₁₀ 到 255₁₀
- 十六进制范围:00₁₆ 到 FF₁₆
2.2 十六进制编码表
| 十六进制 | 十进制 | 二进制 |
|---|---|---|
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| A | 10 | 1010 |
| B | 11 | 1011 |
| C | 12 | 1100 |
| D | 13 | 1101 |
| E | 14 | 1110 |
| F | 15 | 1111 |
2.3 C语言中的十六进制表示
// 十六进制表示:0xFA1D37B 或 0xfa1d37b
3. 数据类型大小 (Data Representations)
| C数据类型 | 32位系统 | Intel IA32 | x86-64 |
|---|---|---|---|
| char | 1 | 1 | 1 |
| short | 2 | 2 | 2 |
| int | 4 | 4 | 4 |
| long | 4 | 4 | 8 |
| float | 4 | 4 | 4 |
| double | 8 | 8 | 8 |
| long double | - | - | 10/16 |
| pointer | 4 | 4 | 8 |
4. 布尔代数 (Boolean Algebra)
4.1 基本运算
- 与(AND): A&B = 1 当且仅当 A=1 且 B=1
-
或(OR): A B = 1 当 A=1 或 B=1 - 非(NOT): ~A = 1 当 A=0
- 异或(XOR): A^B = 1 当 A=1 或 B=1,但不能同时为1
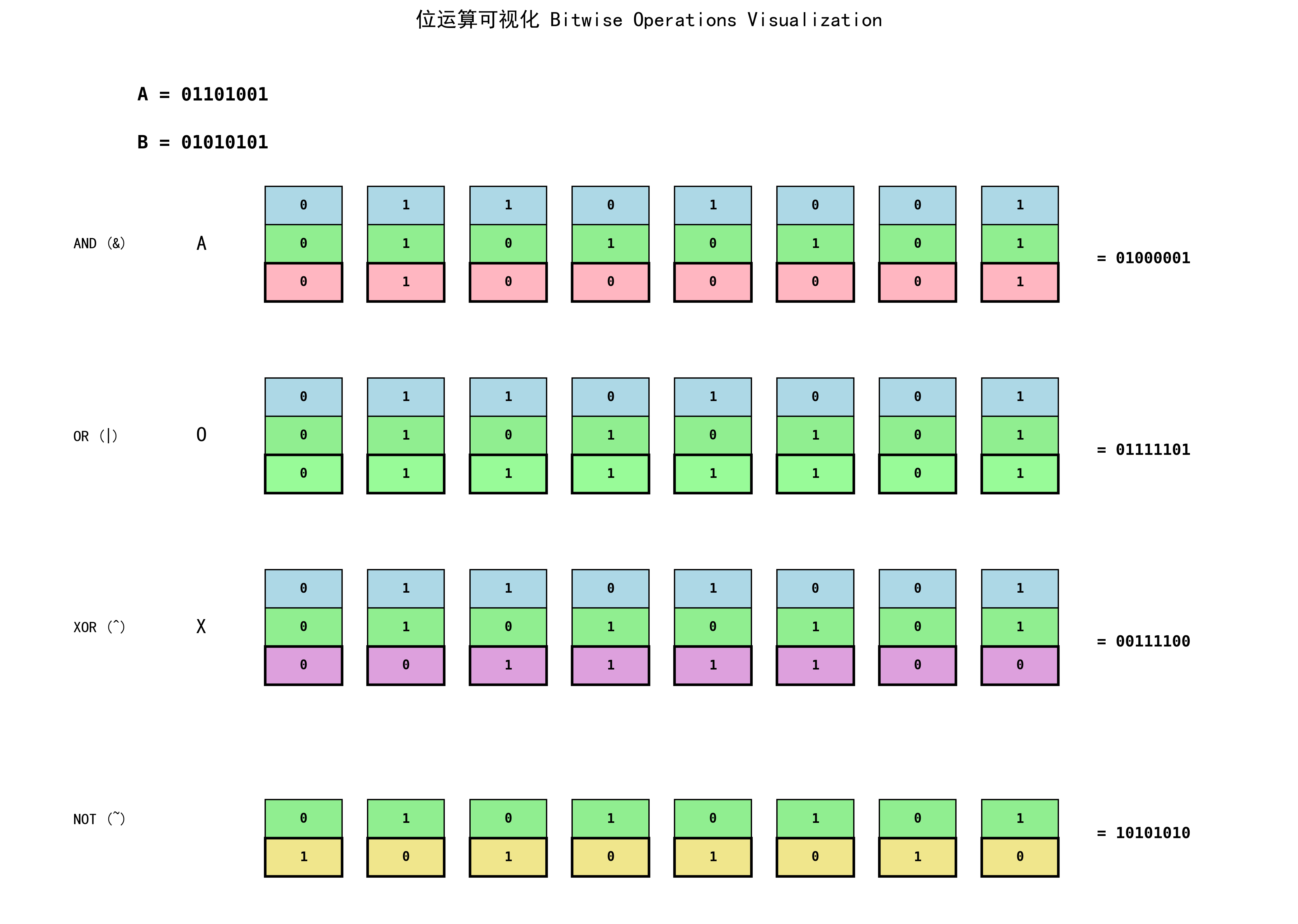
4.2 位向量运算示例
01101001
& 01010101
----------
01000001
01101001
| 01010101
----------
01111101
01101001
^ 01010101
----------
00111100
~ 01010101
----------
10101010
4.3 集合表示
- 用位向量表示集合 {0, 1, 2, …, w-1}
- 01101001₂ 表示集合 {0, 3, 5, 6}
- 01010101₂ 表示集合 {0, 2, 4, 6}
集合运算:
- 交集: & → 01000001₂ = {0, 6}
-
并集: → 01111101₂ = {0, 2, 3, 4, 5, 6} - 对称差: ^ → 00111100₂ = {2, 3, 4, 5}
- 补集: ~ → 10101010₂ = {1, 3, 5, 7}
5. C语言中的位运算
5.1 位级运算符
- 适用于所有整型数据类型:
long,int,short,char,unsigned - 按位操作,将操作数视为位向量
5.2 运算示例
~0x41 → 0xBE // ~01000001₂ → 10111110₂
~0x00 → 0xFF // ~00000000₂ → 11111111₂
0x69 & 0x55 → 0x41 // 01101001₂ & 01010101₂ → 01000001₂
0x69 | 0x55 → 0x7D // 01101001₂ | 01010101₂ → 01111101₂
5.3 逻辑运算符对比
位运算符 vs 逻辑运算符:
-
&,|,~vs&&,||,! - 逻辑运算符:0为False,非0为True,结果只有0或1
- 支持短路求值
!0x41 → 0x00 // 逻辑非
!0x00 → 0x01 // 逻辑非
!!0x41 → 0x01 // 双重逻辑非
0x69 && 0x55 → 0x01 // 逻辑与
p && *p // 避免空指针访问
⚠️ 注意:区分 && 与 &,|| 与 | - 这是C编程中的常见错误!
6. 移位运算 (Shift Operations)
6.1 左移:x « y
- 将位向量x向左移动y位
- 左边多余的位丢弃,右边补0
6.2 右移:x » y
- 将位向量x向右移动y位
- 右边多余的位丢弃
- 逻辑右移:左边补0
- 算术右移:左边复制最高有效位(符号位)
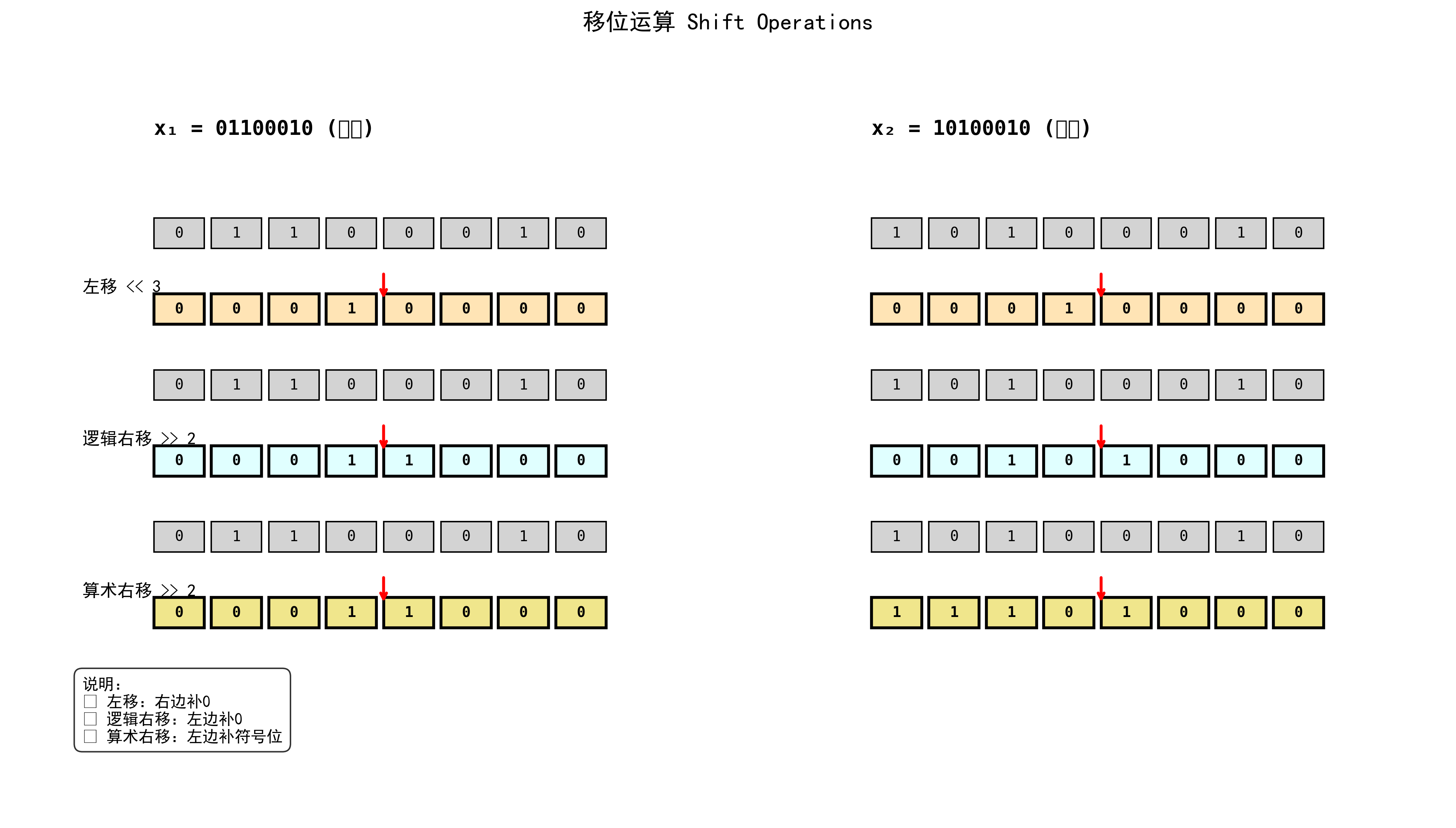
6.3 移位示例
| 操作 | x=01100010 | x=10100010 |
|---|---|---|
| « 3 | 00010000 | 00010000 |
| 逻辑 » 2 | 00011000 | 00101000 |
| 算术 » 2 | 00011000 | 11101000 |
⚠️ 未定义行为:移位量 < 0 或 ≥ 字长
7. 整数表示 (Integer Representations)
7.1 无符号整数 (Unsigned)
\[B2U(X) = \sum_{i=0}^{w-1} x_i \cdot 2^i\]7.2 补码整数 (Two’s Complement)
\[B2T(X) = -x_{w-1} \cdot 2^{w-1} + \sum_{i=0}^{w-2} x_i \cdot 2^i\]7.3 示例:short int (16位)
short int x = 15213; // 0011 1011 0110 1101
short int y = -15213; // 1100 0100 1001 0011
| 变量 | 十进制 | 十六进制 | 二进制表示 |
|---|---|---|---|
| x | 15213 | 3B 6D | 00111011 01101101 |
| y | -15213 | C4 93 | 11000100 10010011 |
7.4 数值范围
对于w位数:
- 无符号: UMin = 0, UMax = 2ʷ - 1
- 补码: TMin = -2ʷ⁻¹, TMax = 2ʷ⁻¹ - 1
16位示例:
- UMax = 65535, TMax = 32767, TMin = -32768
- 特殊值:-1 = 0xFFFF (全1)
观察:
-
TMin = TMax + 1 (不对称范围) - UMax = 2 × TMax + 1
8. 类型转换 (Conversion and Casting)
8.1 有符号↔无符号转换
- 保持位模式不变,重新解释含义
- 负数转换为大的正数
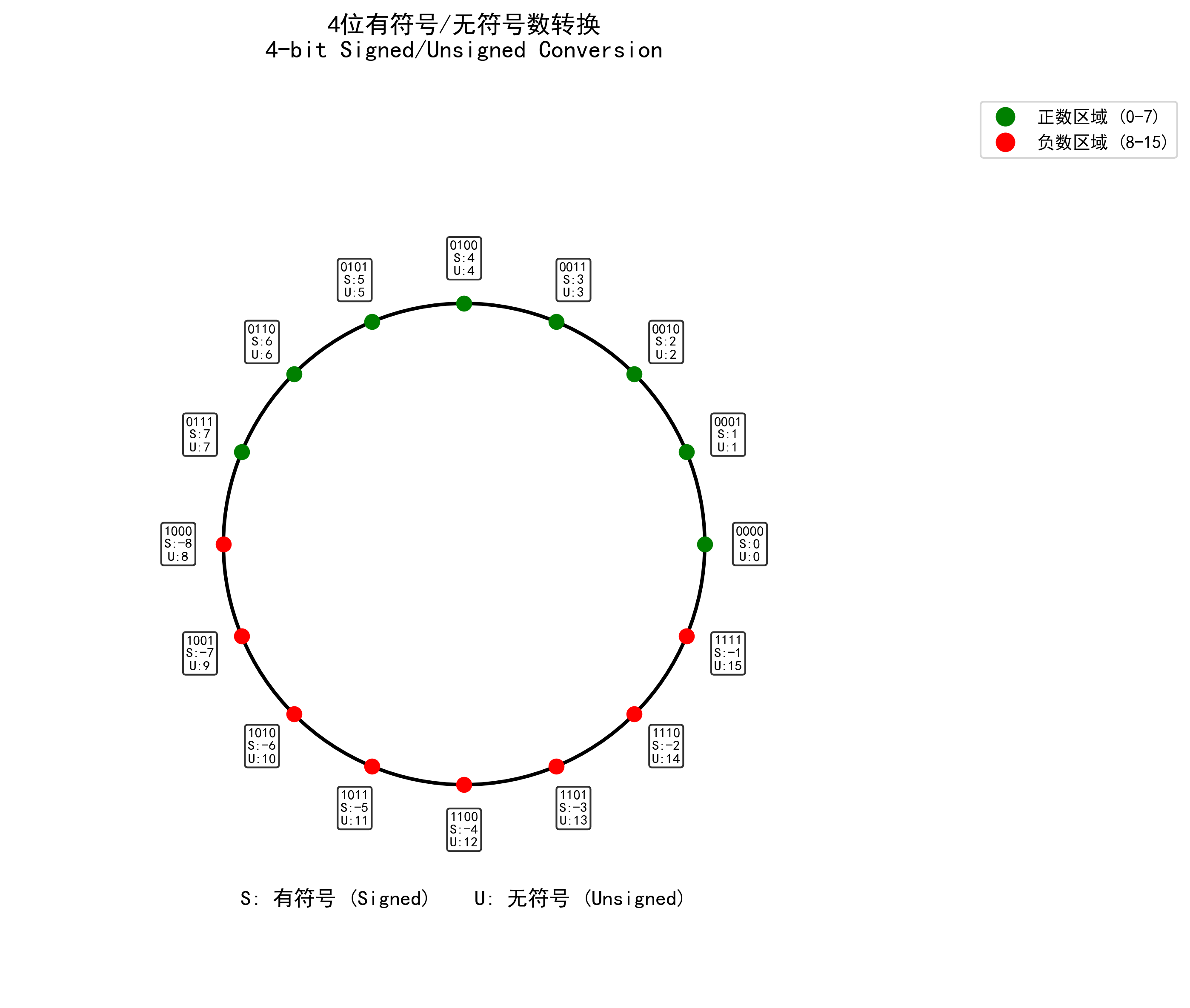
8.2 转换可视化
对于4位数系统:
| 位模式 | 有符号 | 无符号 |
|---|---|---|
| 0000 | 0 | 0 |
| 0001 | 1 | 1 |
| 0111 | 7 | 7 |
| 1000 | -8 | 8 |
| 1111 | -1 | 15 |
8.3 C语言中的转换
// 常量
0U, 4294967259U // 无符号后缀
// 显式转换
int tx, ty;
unsigned ux, uy;
tx = (int) ux;
uy = (unsigned) ty;
// 隐式转换
tx = ux;
uy = ty;
8.4 转换陷阱
// 混合表达式中,有符号数会被隐式转换为无符号数
-1 < 0U // False! -1被转换为4294967295U
9. 扩展和截断 (Expanding & Truncating)
9.1 符号扩展 (Sign Extension)
将w位有符号整数转换为w+k位:
- 规则:复制k个符号位
- 示例:01010 → 00001010 (正数前面补0)
- 示例:10110 → 11110110 (负数前面补1)
9.2 截断 (Truncation)
- 无符号/有符号:直接截断高位
- 结果重新解释
- 无符号:相当于 mod 2ᵏ 运算
- 有符号:类似于 mod 运算
9.3 C语言自动处理
short int x = 15213;
int ix = (int) x; // 自动符号扩展
10. 整数运算 (Integer Arithmetic)
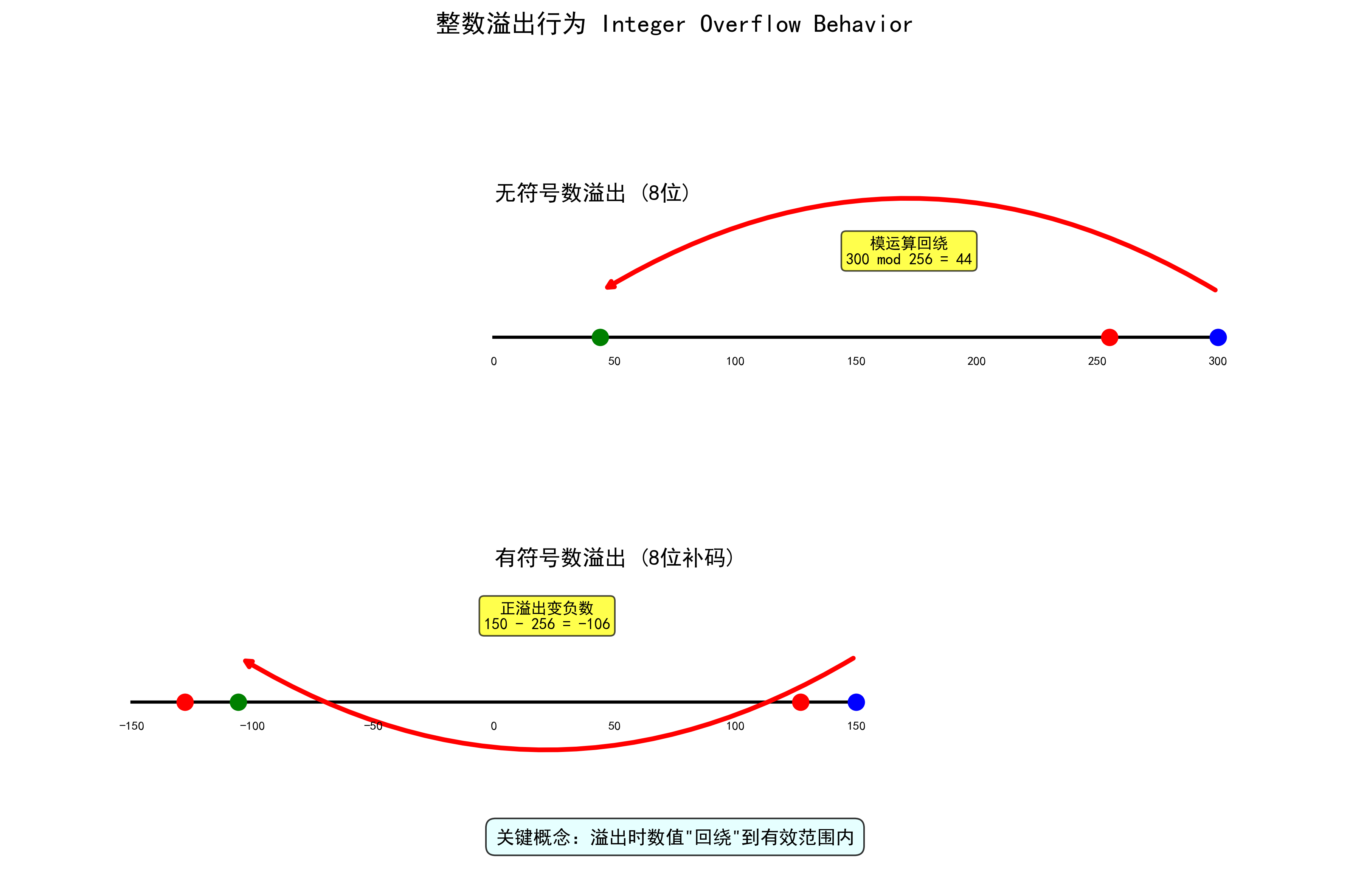
10.1 无符号加法
- 模运算:UAddw(u,v) = (u + v) mod 2ʷ
- 溢出时结果”回绕”
10.2 补码加法
- 位级行为与无符号加法相同
- 可能发生正溢出或负溢出
10.3 乘法
- 无符号:UMultw(u,v) = (u × v) mod 2ʷ
- 有符号:位级下w位与无符号相同
10.4 2的幂次运算优化
// 乘法优化
u << k // 等价于 u * 2^k
// 除法优化
u >> k // 等价于 u / 2^k (无符号)
⭐ 重要教训:相信编译器的优化!
11. 内存表示 (Memory Representations)
11.1 字节序 (Byte Ordering)
大端序 (Big Endian):
- 最低有效字节在最高地址
- 用于:Sun, PPC Mac, Internet
小端序 (Little Endian):
- 最低有效字节在最低地址
- 用于:x86, ARM (Android, iOS, Windows)
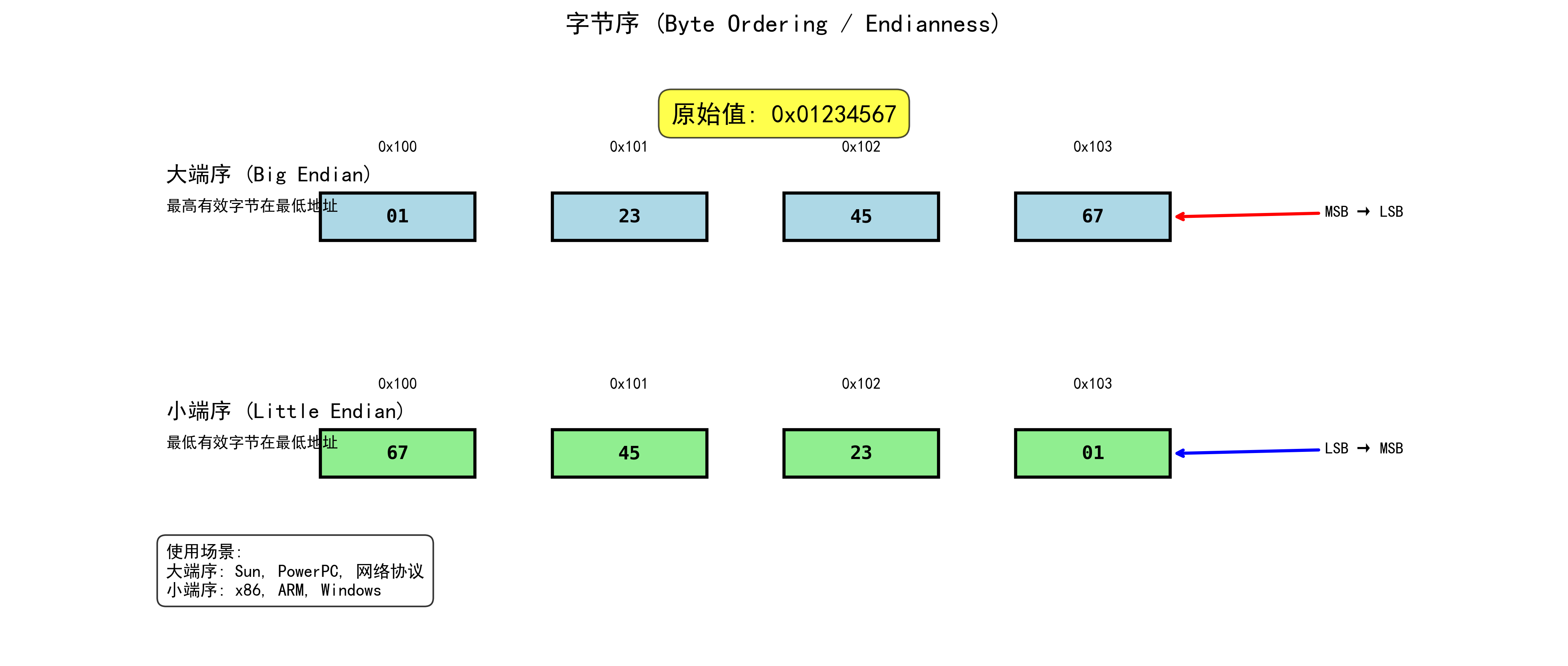
11.2 示例:0x01234567
地址: 0x100 0x101 0x102 0x103
大端序: 01 23 45 67
小端序: 67 45 23 01
11.3 字符串表示
- 使用ASCII编码
- 字符’0’ = 0x30, 字符’1’ = 0x31
- 以null字符(0x00)结尾
- 字节序无关
12. 编程建议
12.1 无符号数使用场景
应该使用:
- 模运算
- 位集合表示
谨慎使用:
- 容易出错的循环
// 错误示例
unsigned i;
for (i = cnt-2; i >= 0; i--) // 无限循环!
// 正确示例
unsigned i;
for (i = cnt-2; i < cnt; i--) // 利用回绕特性
12.2 C语言陷阱
// sizeof返回size_t (无符号类型)
#define DELTA sizeof(int)
for (i = CNT; i-DELTA >= 0; i-= DELTA) // 可能出错
总结要点:
- 理解位级表示的重要性
- 掌握有符号/无符号转换规则
- 注意整数运算的溢出行为
- 谨慎使用无符号类型
- 了解不同架构的字节序差异
Enjoy Reading This Article?
Here are some more articles you might like to read next: