人工智能中的编程 - 第6章: 矩阵乘法(Matrix Product)
矩阵乘法的重要性
矩阵乘法是数学和深度学习中的基础运算,在神经网络的各个组件中扮演核心角色:
深度学习中的应用
全连接层(Fully Connected Layers):
- 前向传播:$Y_{m \times n} = W_{m \times k} \times X_{k \times n}$
- 反向传播:$\frac{\partial L}{\partial X_{k \times n}} = W_{m \times k}^T \times \frac{\partial L}{\partial y_{m \times n}}$
- 权重梯度:$\frac{\partial L}{\partial W_{m \times k}} = \frac{\partial L}{\partial y_{m \times n}} \times X_{k \times n}^T$
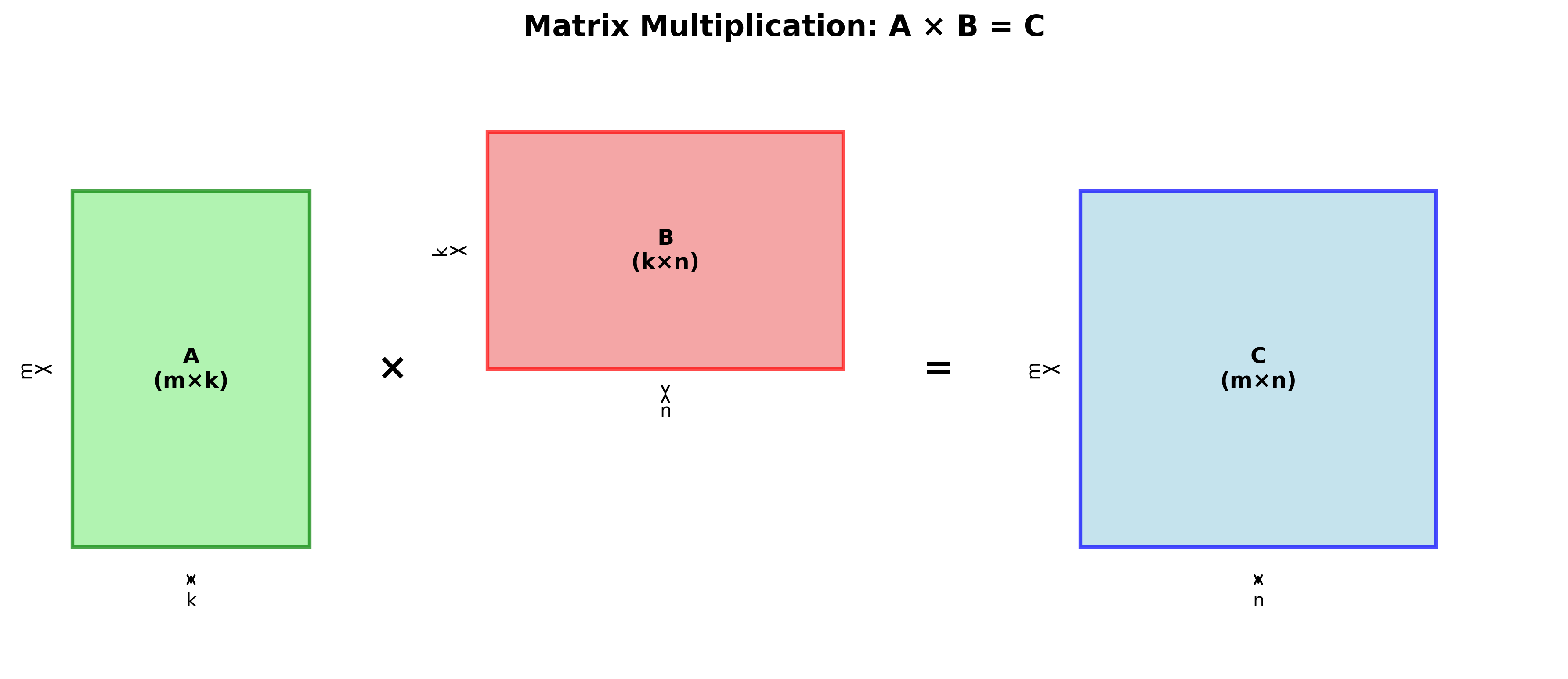
基本矩阵乘法运算: \(c_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{in}b_{nj} = \sum_{k=1}^n a_{ik}b_{kj}\)
CPU上的矩阵乘法
通用矩阵乘法(GEMM)
GEMM运算形式:$C = \alpha A \times B + \beta C$
void sgemm_cpu(
int M, int N, int K, float alpha, const float *A,
const float *B, float beta, float *C) {
for (int row = 0; row < M; row++) {
for (int col = 0; col < N; col++) {
float sum = 0.0;
for (int i = 0; i < K; i++) {
sum += A[row * K + i] * B[i * N + col];
}
C[row * N + col] =
alpha * sum + beta * C[row * N + col];
}
}
}
复杂度分析:
- 三重嵌套循环
- 工作复杂度:$O(MNK)$
GPU上的矩阵乘法
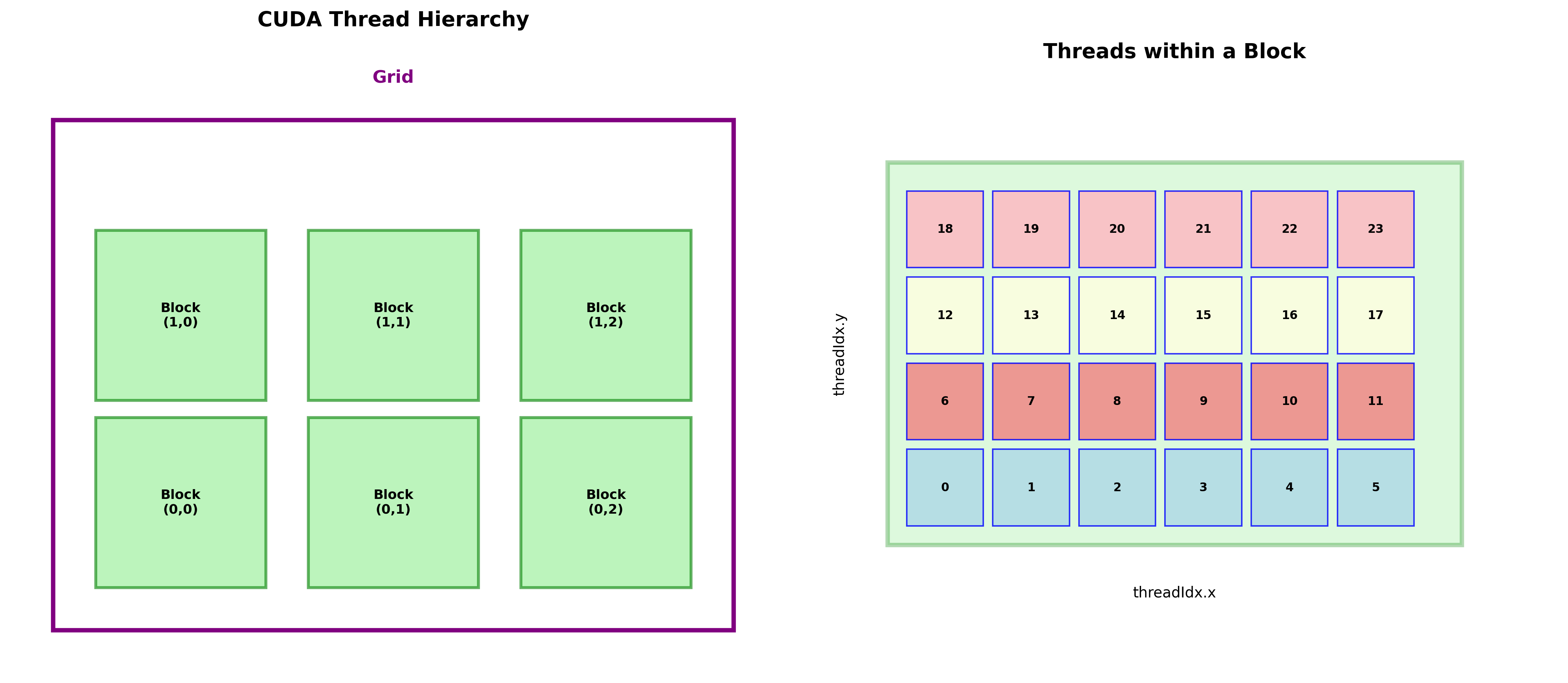
朴素实现(Naive Implementation)
每个线程负责计算矩阵C中的一个元素:
__global__ void sgemm_naive(
int M, int N, int K, float alpha, const float *A,
const float *B, float beta, float *C) {
const int row = blockIdx.x * blockDim.x + threadIdx.x;
const int col = blockIdx.y * blockDim.y + threadIdx.y;
if (row < M && col < N) {
float sum = 0.0;
for (int k = 0; k < K; k++) {
sum += A[row * K + k] * B[k * N + col];
}
C[row * N + col] = alpha * sum + beta * C[row * N + col];
}
}
执行配置:
dim3 gridDim(Ceil(M, 32), Ceil(N, 32)), blockDim(32, 32);
sgemm_naive<<<gridDim, blockDim>>>(M, N, K, alpha, A, B, beta, C);
块量化问题(Tile Quantization)
朴素实现存在的问题:
- 当矩阵大小不是块大小的整数倍时,边界块中的大量线程处于空闲状态
- 造成计算资源浪费

内存访问优化
线程布局优化
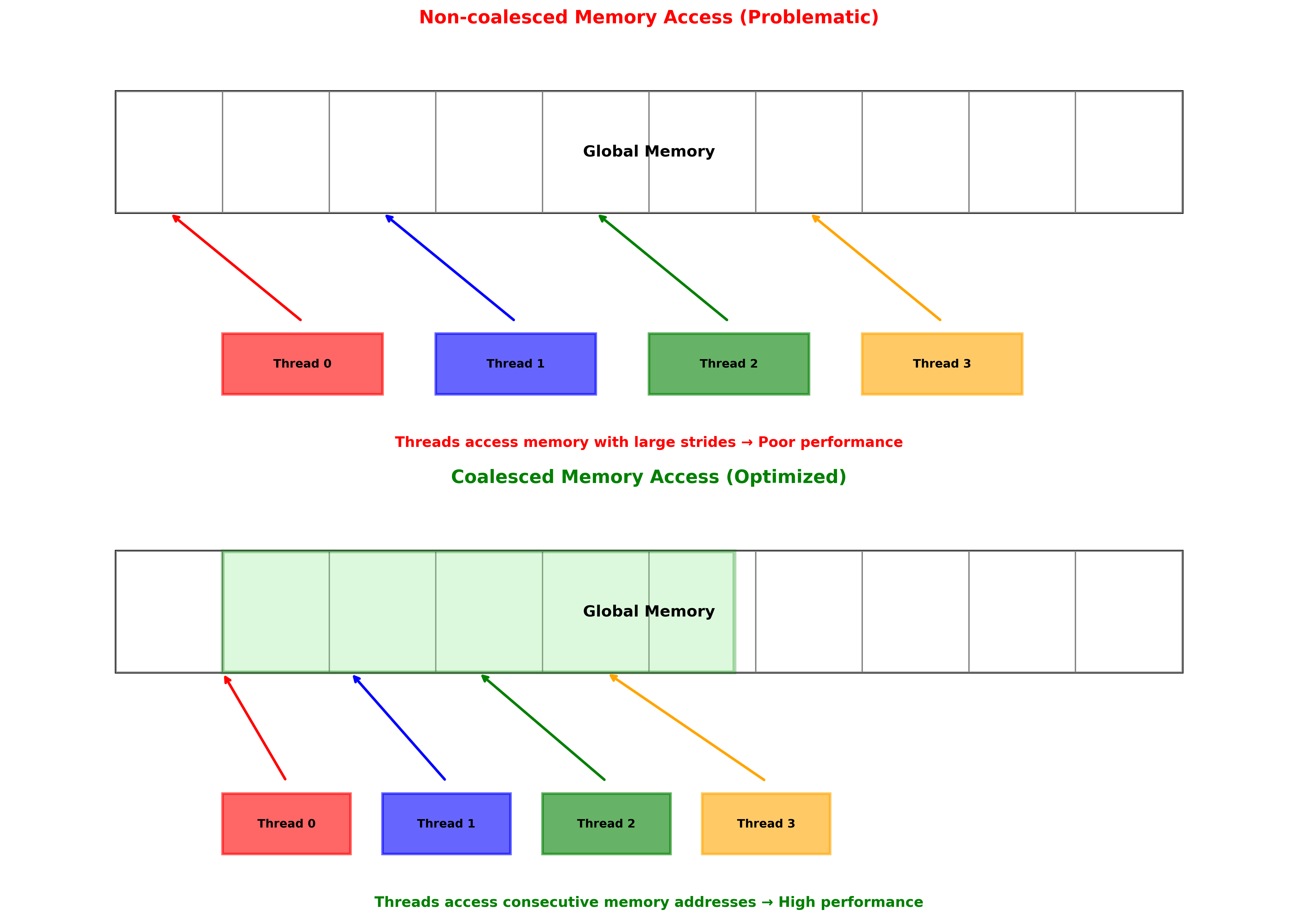
问题分析:
- 不同线程访问相同列数据时产生非连续内存访问
- 需要调整线程布局以实现合并访问
合并访问实现(Coalescing Access)
__global__ void sgemm_coalesce(
int M, int N, int K, float alpha, const float *A,
const float *B, float beta, float *C) {
const int col = blockIdx.x * blockDim.x + threadIdx.x % 32;
const int row = blockIdx.y * blockDim.y + threadIdx.x / 32;
if (row < M && col < N) {
float sum = 0.0;
for (int k = 0; k < K; k++) {
sum += A[col * K + k] * B[k * N + row];
}
C[row * N + col] = alpha * sum + beta * C[row * N + col];
}
}
配置调整:
dim3 gridDim(Ceil(N, 32), Ceil(M, 32)), blockDim(32 * 32);
性能提升:比朴素实现快约8倍
Roofline性能模型
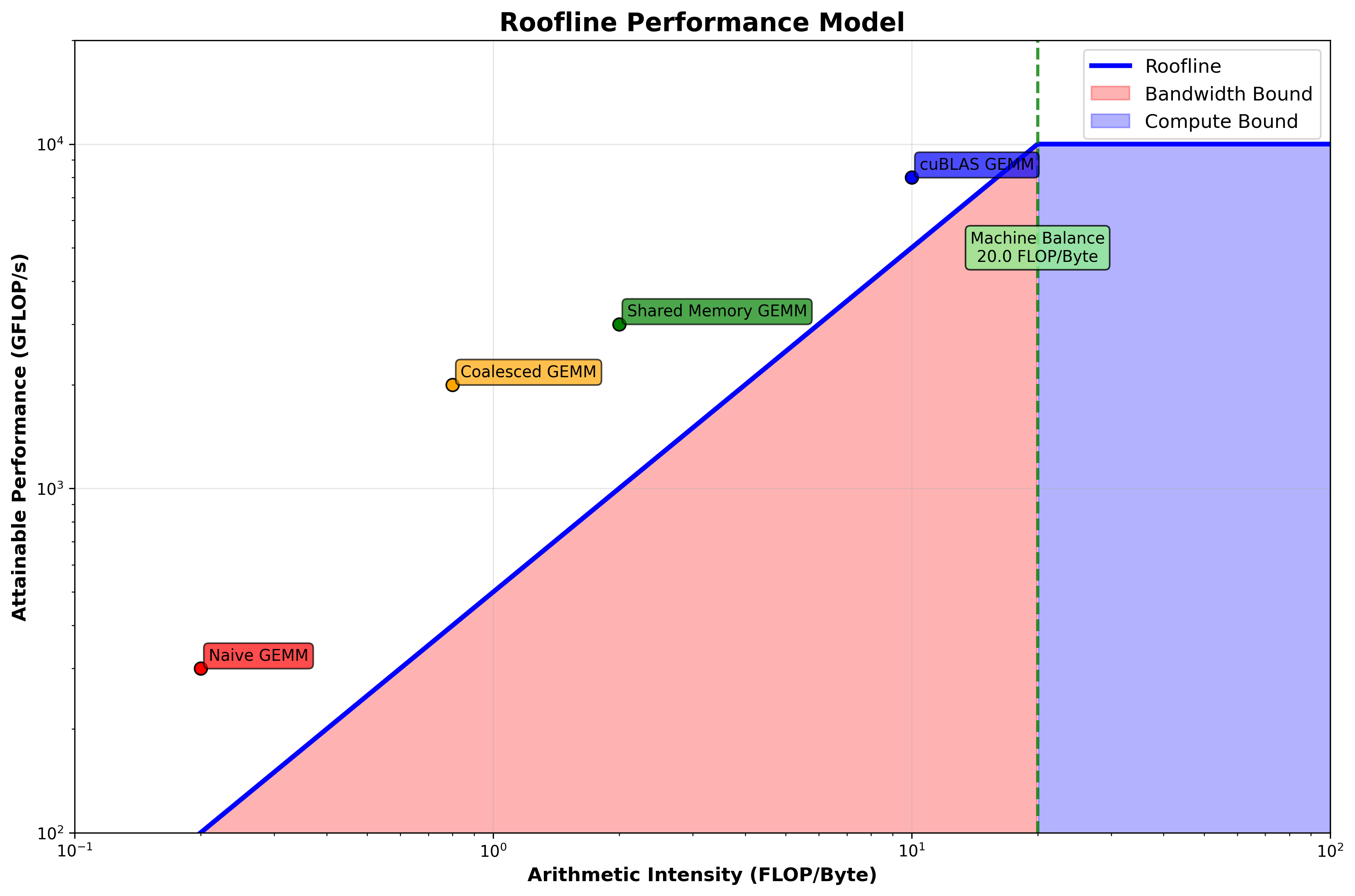
性能瓶颈分析
带宽限制(Bandwidth Bound):
- 受内存系统数据传输速度限制
计算限制(Compute Bound):
- 受计算能力限制,当算术强度高于机器平衡点时
GPU程序特点:
- 通常(但不总是)受带宽限制
- 需要提高内存效率
共享内存优化
块状矩阵乘法
核心思想:
- 将A和B的块从全局内存加载到共享内存
- 每个线程仍负责C中的一个元素
- 沿A的列和B的行移动数据块
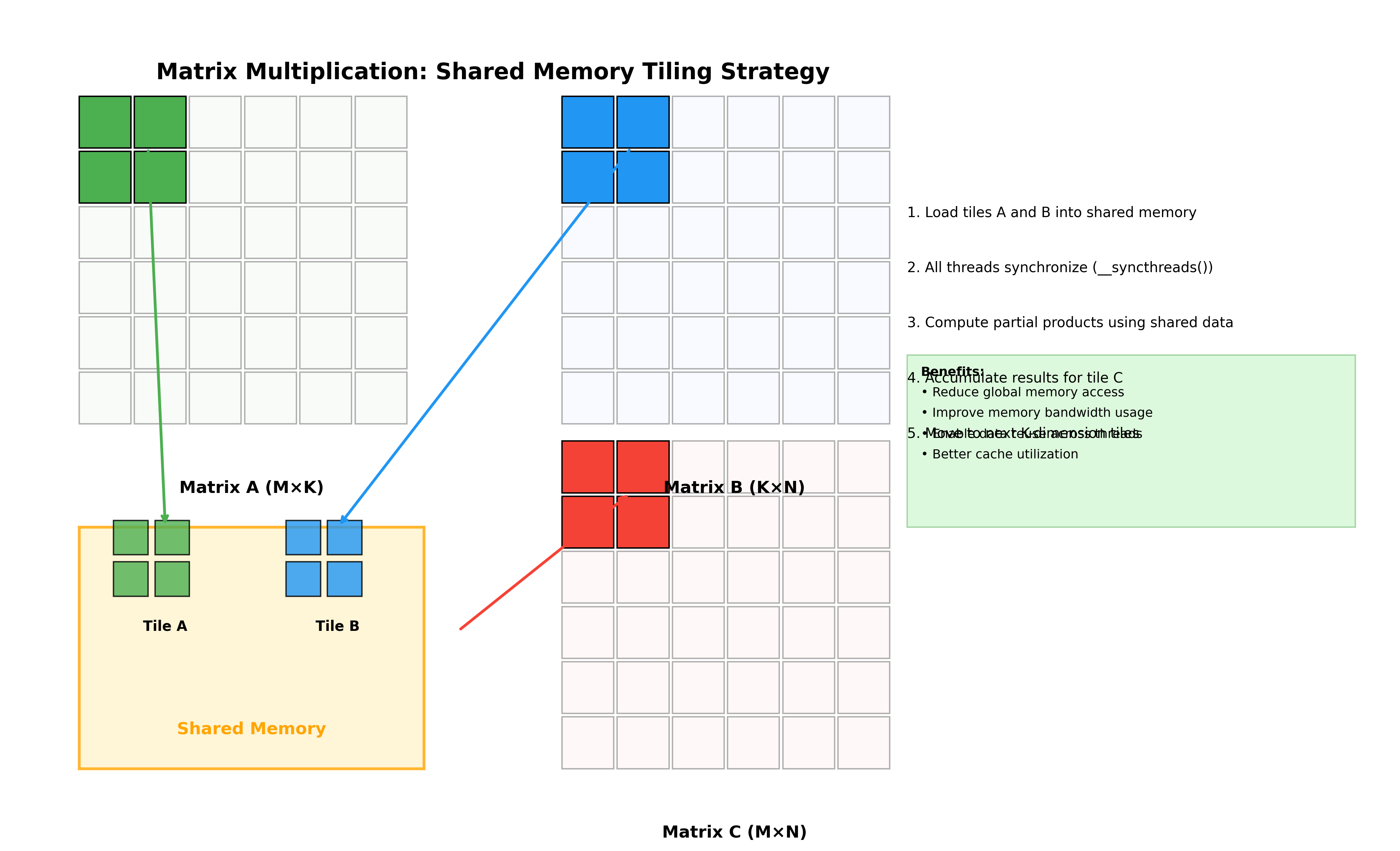
共享内存实现
__global__ void sgemm_shared_memory(
int M, int N, int K, float alpha, const float *A,
const float *B, float beta, float *C) {
__shared__ float As[BLOCKSIZE * BLOCKSIZE];
__shared__ float Bs[BLOCKSIZE * BLOCKSIZE];
const int cRow = blockIdx.x, cCol = blockIdx.y;
const uint threadCol = threadIdx.x % BLOCKSIZE;
const uint threadRow = threadIdx.x / BLOCKSIZE;
// 调整指针到起始位置
A += cRow * BLOCKSIZE * K;
B += cCol * BLOCKSIZE;
C += cRow * BLOCKSIZE * N + cCol * BLOCKSIZE;
float tmp = 0.0;
for (int bkIdx = 0; bkIdx < K; bkIdx += BLOCKSIZE) {
// 加载数据到共享内存
As[threadRow * BLOCKSIZE + threadCol] = A[threadRow * K + threadCol];
Bs[threadRow * BLOCKSIZE + threadCol] = B[threadRow * N + threadCol];
__syncthreads();
A += BLOCKSIZE;
B += BLOCKSIZE * N;
// 执行点积运算
for (int dotIdx = 0; dotIdx < BLOCKSIZE; ++dotIdx) {
tmp += As[threadRow * BLOCKSIZE + dotIdx] *
Bs[dotIdx * BLOCKSIZE + threadCol];
}
__syncthreads();
}
C[threadRow * N + threadCol] =
alpha * tmp + beta * C[threadRow * N + threadCol];
}
性能对比
| 实现方式 | GFLOP/s | 相对cuBLAS性能 |
|---|---|---|
| 朴素实现 | 309.0 | 1.3% |
| 合并访问 | 1986.5 | 8.5% |
| 共享内存 | 2980.3 | 12.8% |
内存限制:
- 共享内存资源有限
- 一个SM通常有100KB共享内存
- 示例中使用了8KB共享内存(1024 × 2 × 4字节)
稀疏矩阵
稀疏矩阵的应用
稀疏矩阵广泛应用于:
- 三角网格处理
- 图神经网络
- 科学计算
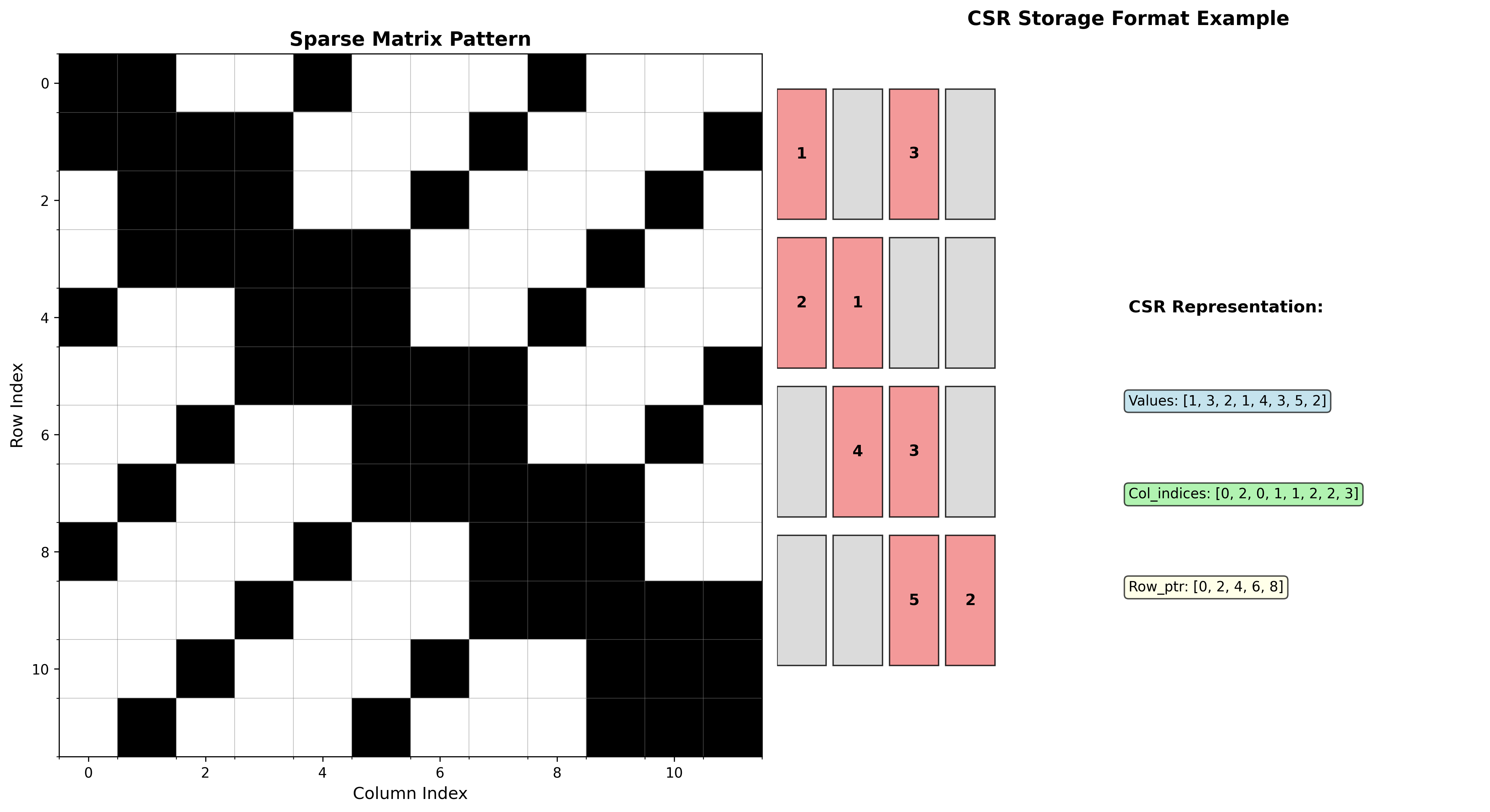
存储格式
坐标列表格式(COO):
矩阵: [5 0 0 0] V = [5 8 3 6]
[0 8 0 0] COL_INDEX = [0 1 2 1]
[0 0 3 0] ROW_INDEX = [0 1 2 3]
[0 6 0 0]
压缩稀疏行格式(CSR):
矩阵: [10 20 0 0 0 0] V = [10 20 30 40 50 60 70 80]
[ 0 30 0 40 0 0] COL_INDEX = [0 1 1 3 2 3 4 5]
[ 0 0 50 60 70 0] ROW_INDEX = [0 2 4 7 8]
[ 0 0 0 0 0 80]
PyTorch稀疏张量
COO格式示例:
>>> i = [[0, 1, 1],
[2, 0, 2]]
>>> v = [3, 4, 5]
>>> s = torch.sparse_coo_tensor(i, v, (2, 3))
>>> s.to_dense()
tensor([[0, 0, 3],
[4, 0, 5]])
CSR格式示例:
>>> crow_indices = torch.tensor([0, 2, 4])
>>> col_indices = torch.tensor([0, 1, 0, 1])
>>> values = torch.tensor([1, 2, 3, 4])
>>> csr = torch.sparse_csr_tensor(crow_indices, col_indices, values,
dtype=torch.float64)
>>> csr.to_dense()
tensor([[1., 2.],
[3., 4.]], dtype=torch.float64)
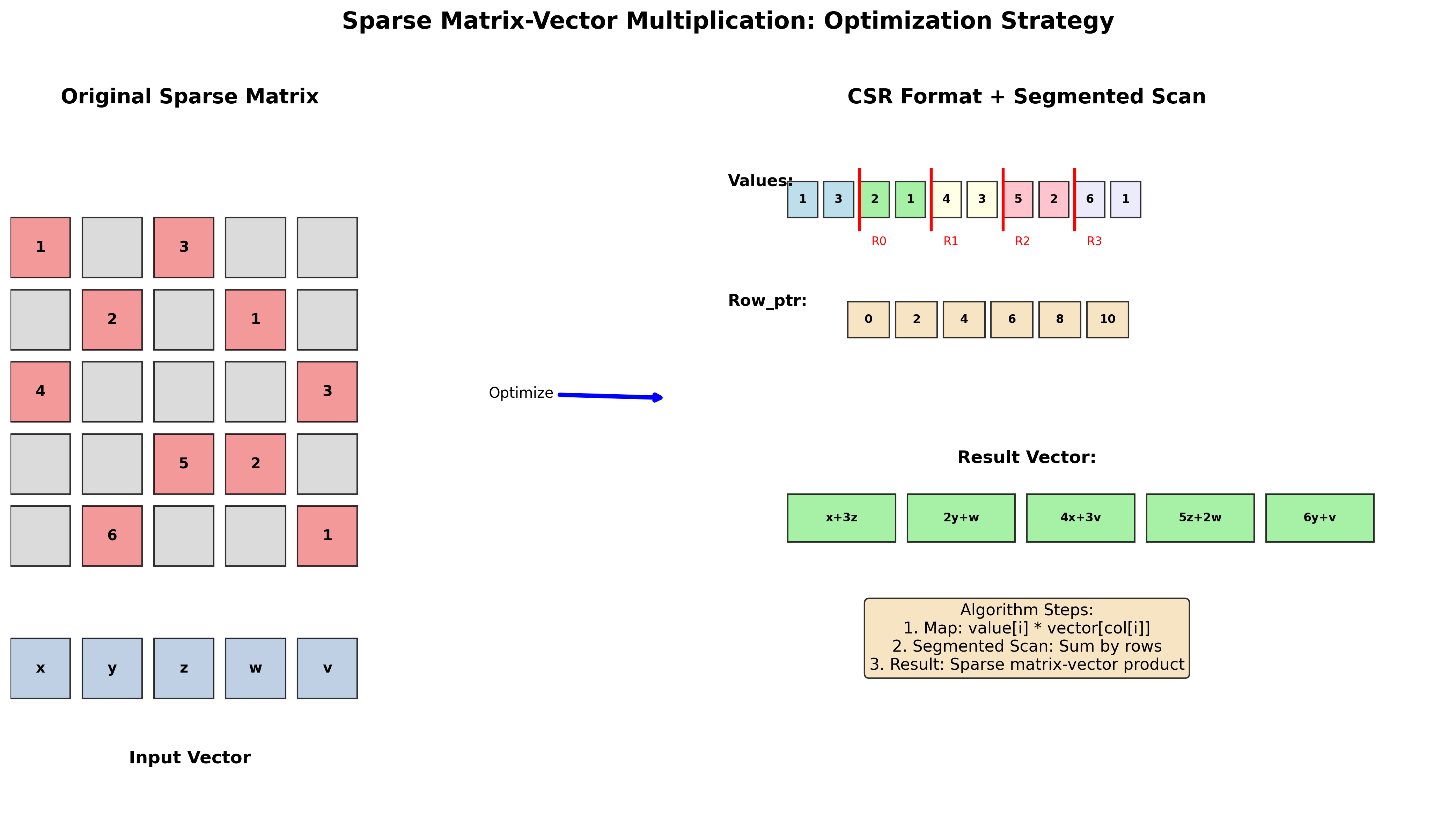
稀疏矩阵-向量乘法
算法步骤:
- 映射操作:计算标量积 Value × Column × X
- 分段扫描:使用cRow进行分段求和
示例:
稀疏矩阵: [1 0 3] 向量: [x] 结果: [x + 3z]
[2 1 0] [y] [2x + y]
[0 4 3] [z] [4y + 3z]
Value: [1, 3, 2, 1, 4, 3]
Column: [0, 2, 0, 1, 1, 2]
cRow: [0, 2, 5, 6]
优化策略:将矩阵分解为Reduce和分段扫描操作
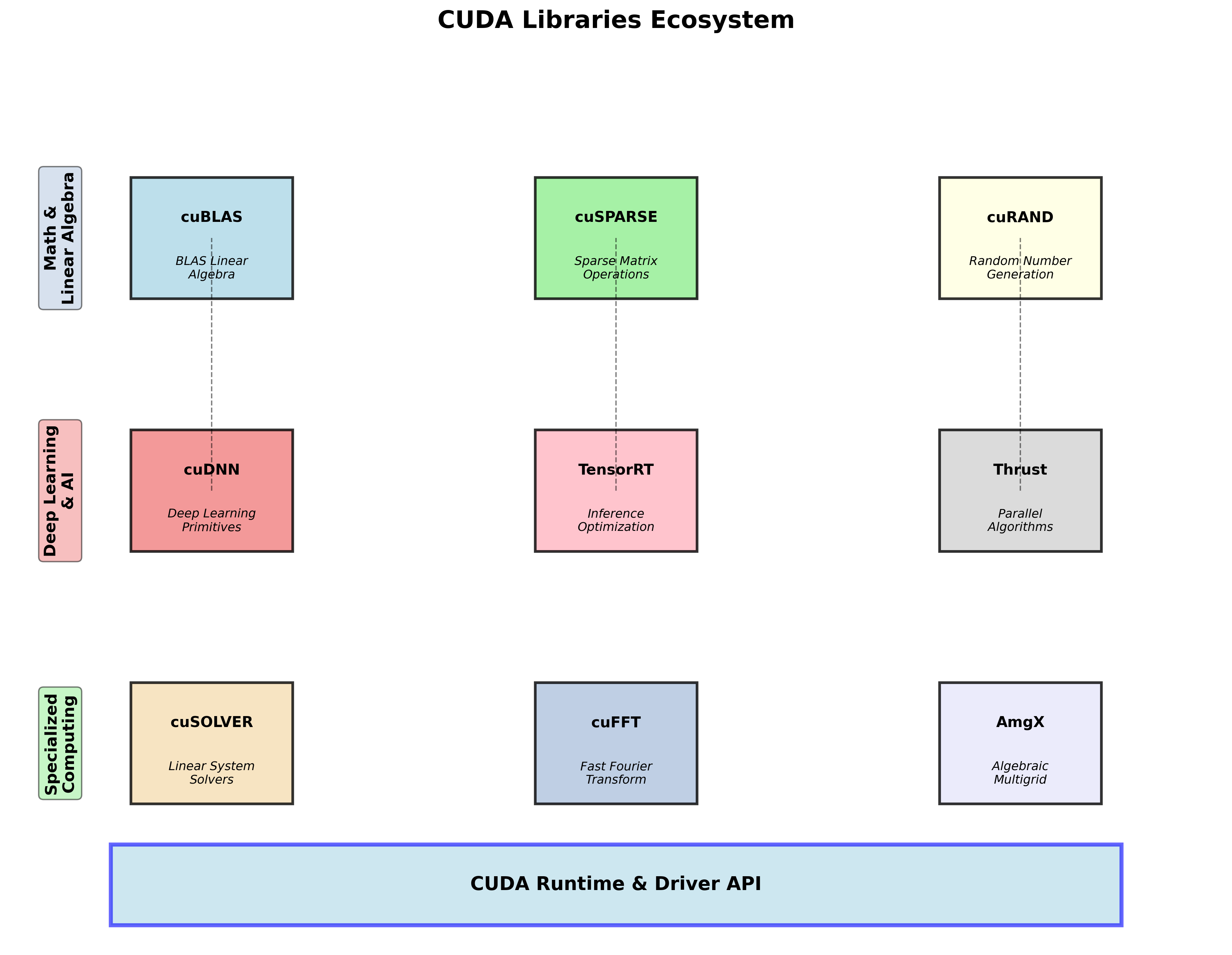
CUDA线性代数库
CUDA库家族
CUDA编程语言:
- Thrust:基于STL的C++模板库
CUDA深度学习库:
- cuDNN:大多数开源深度学习框架的GPU组件
- TensorRT:高性能深度学习推理优化器和运行时
CUDA线性代数和数学库:
- cuBLAS:GPU加速的BLAS库,是GPU矩阵运算的最高性能实现
- cuSPARSE:处理稀疏矩阵
- cuRAND:GPU加速的随机数生成器
Thrust库
特性:
- 基于标准模板库(STL)的C++模板库
- 提供丰富的数据并行原语集合:scan、sort、reduce
- 可组合实现复杂算法,代码简洁易读
向量操作示例:
#include <thrust/device_vector.h>
#include <thrust/host_vector.h>
int main(void) {
thrust::host_vector<int> H(4);
H[0] = 14; H[1] = 20; H[2] = 38;
// 复制到设备
thrust::device_vector<int> D = H;
// 修改元素
D[0] = 99; D[1] = 88;
return 0;
}
Map操作实现:
#include <thrust/transform.h>
// 计算 Y = -X
thrust::transform(X.begin(), X.end(), Y.begin(),
thrust::negate<int>());
// 自定义操作类
class Saxpy {
public:
const float a;
Saxpy(float _a) : a(_a) {}
__host__ __device__ float operator()(const float& x, const float& y) const {
return a * x + y;
}
};
// Y <- A * X + Y
thrust::transform(X.begin(), X.end(), Y.begin(), Y.begin(), Saxpy(A));
其他操作:
// 归约操作
#include <thrust/reduce.h>
int sum = thrust::reduce(D.begin(), D.end(), (int) 0, thrust::plus<int>());
// 扫描操作
#include <thrust/scan.h>
thrust::inclusive_scan(data, data + 6, data);
thrust::exclusive_scan(data, data + 6, data);
// 排序操作
#include <thrust/sort.h>
thrust::sort(A, A + N);
BLAS(基础线性代数子程序)
BLAS层次结构
Level 1:向量操作,线性时间复杂度
- 点积、向量范数
- AXPY运算:$y \leftarrow \alpha x + y$
Level 2:矩阵-向量操作,二次时间复杂度
- 通用矩阵-向量乘法(GEMV):$y \leftarrow \alpha Ax + \beta y$
Level 3:矩阵-矩阵操作,三次时间复杂度
- 通用矩阵乘法(GEMM):$C \leftarrow \alpha AB + \beta C$
cuBLAS使用示例
基本使用模式:
// 步骤1:创建cuBLAS句柄
cublasHandle_t handle;
cublasCreate(&handle);
// 步骤2:调用SGEMM
cublasSgemm(handle, ...<options>..);
// 步骤3:销毁句柄
cublasDestroy(handle);
GEMM实现示例:
#include <cublas_v2.h>
void gemm_gpu(const float *A, const float *B, float *C,
const int m, const int k, const int n) {
int lda = m, ldb = k, ldc = m;
const float alf = 1, bet = 0;
const float *alpha = &alf, *beta = &bet;
cublasHandle_t handle;
cublasCreate(&handle);
cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_N, m, n, k, alpha,
A, lda, B, ldb, beta, C, ldc);
cublasDestroy(handle);
}
cuRAND使用示例
#include <curand.h>
void matrix_init(float *A, int rows, int cols) {
curandGenerator_t prng;
curandCreateGenerator(&prng, CURAND_RNG_PSEUDO_DEFAULT);
curandSetPseudoRandomGeneratorSeed(prng,
(unsigned long long)clock());
curandGenerateUniform(prng, A, rows * cols);
curandDestroyGenerator(prng);
}
全连接层实现
PyTorch中的全连接层
张量形状变换:
- 图像特征张量形状:[N, H, W, C] 或 [N, C, H, W]
- 使用
torch.view、torch.reshape、torch.flatten变换为[N, -1]
全连接层使用:
# 使用torch.nn.Linear(而非torch.nn.functional.linear)
# torch.nn.Linear帮助优化权重
layer = torch.nn.Linear(in_features, out_features, bias=True)
CUDA实现
前向传播:
void forward_fc(float* input, float* output, float* weights, float* bias,
int batch_size, int in_features, int out_features) {
// 矩阵乘法
gemm_gpu(CublasNoTrans, CublasTrans, batch_size, out_features, in_features,
1.0, input, weight, 0.0, output);
// 添加偏置
gemm_gpu(CublasNoTrans, CublasNoTrans, batch_size, out_features, 1,
1.0, ones_, bias, 1.0, output);
}
全连接层的优缺点
优点:
- 表达能力强
- 可以用GEMM轻松实现
缺点:
- 需要大量参数(例如:200×200→1000的FC层需要200M参数)
- 缺乏平移不变性
深度学习中的矩阵运算
以AlexNet为例,神经网络包含多种运算类型:
- 卷积层(Convolution)
- 最大池化(Max Pooling)
- 全连接层(Fully Connected Layer)
- Softmax和损失函数
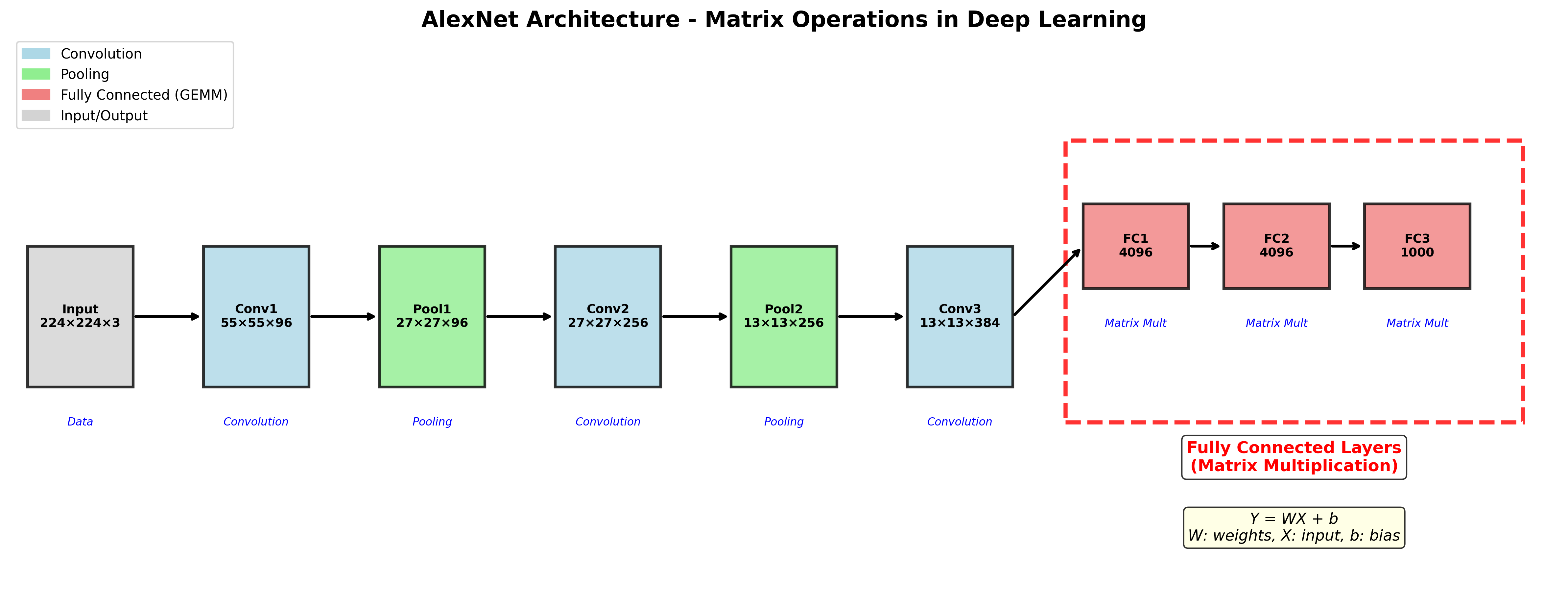
全连接层在神经网络的最后阶段起到分类器的作用,通过矩阵乘法将特征映射到输出类别。
总结
矩阵乘法优化要点
- 内存访问优化:合并访问比分散访问更重要
- 共享内存利用:通过数据局部性减少全局内存访问
- 线程布局设计:避免warp内的分歧和空闲线程
- 库函数使用:cuBLAS提供高度优化的实现
CUDA生态系统价值
CUDA线性代数和数学库为高性能GPU应用程序提供了重要基础:
- cuBLAS:矩阵运算的黄金标准
- cuSPARSE:稀疏矩阵运算支持
- Thrust:简化并行算法开发
- 深度学习库:为AI应用提供专门优化
这些工具和技术在深度学习、科学计算等领域发挥着关键作用,使得复杂的数值计算能够在GPU上高效执行。
Enjoy Reading This Article?
Here are some more articles you might like to read next: