人工智能中的编程 - 第5章: 并行算法II（Parallel Algorithms II）

并行排序算法

排序是计算机科学中的基础问题，正如Donald Knuth在《计算机程序设计艺术》第3卷中用722页来详述排序和搜索算法。在GPU并行计算中，排序算法的设计面临着独特的挑战和机遇。

砖块排序（Brick Sort）

基本思想

砖块排序本质上是冒泡排序的并行化版本：

复杂度分析：

• 工作复杂度：$O(N^2)$
• 步复杂度：$O(N)$

算法执行过程

砖块排序通过交替执行两种比较模式：

1. 奇偶比较阶段：比较相邻的奇偶位置对
2. 偶奇比较阶段：比较相邻的偶奇位置对

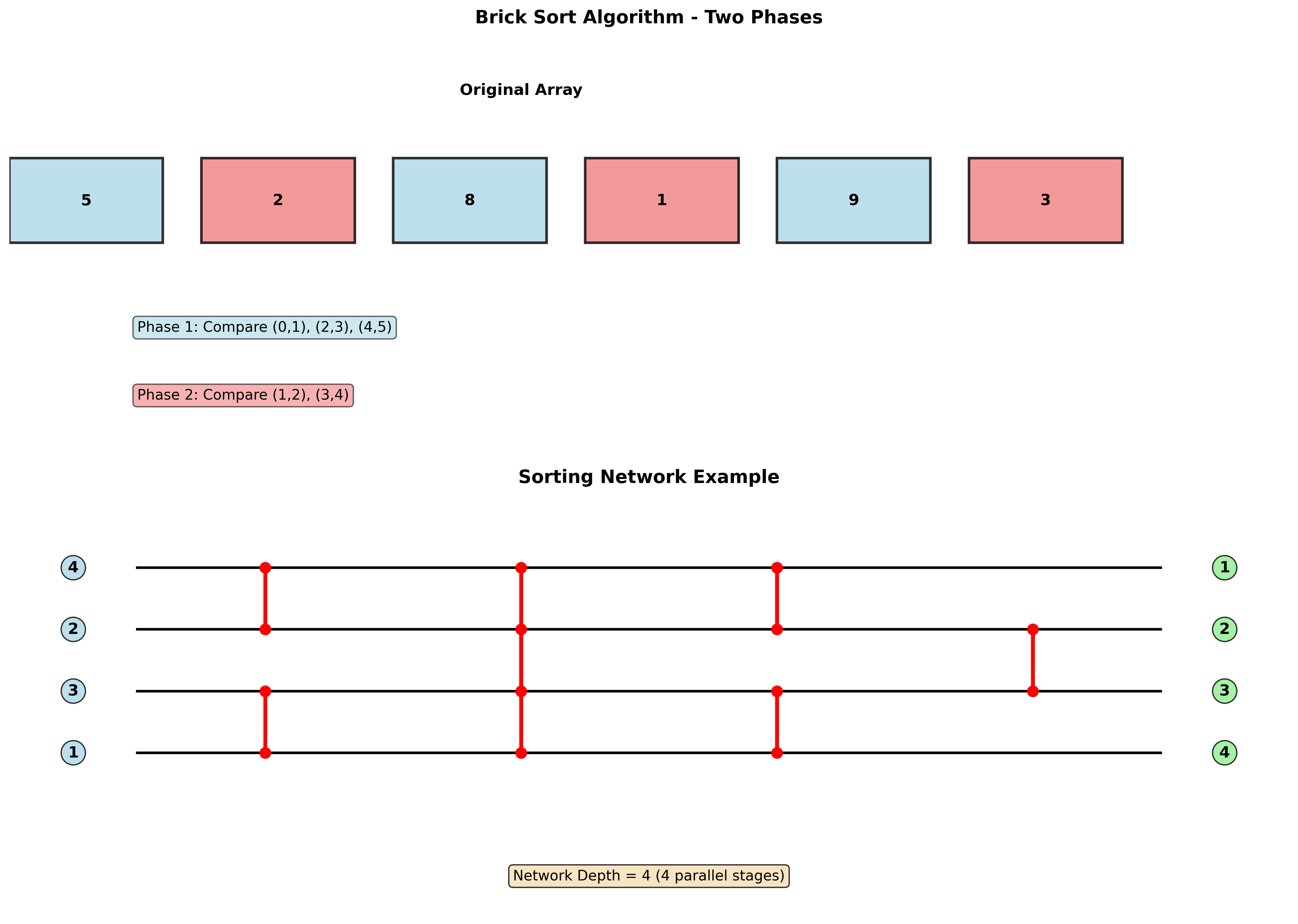
正确性问题：虽然并行化提高了效率，但需要仔细验证算法的正确性。

归并排序（Merge Sort）

分治思想

归并排序基于分治范式，关键在于如何合并两个已排序的数组：

void merge_sort(int *arr, int left, int right) {
    if (left < right) {
        int mid = int((left + right) / 2);
        merge_sort(arr, left, mid);
        merge_sort(arr, mid + 1, right);
        merge(arr, left, mid, right);
    }
}

复杂度：$O(N \log N)$，递推关系为 $T_N = 2T_{N/2} + N$

GPU上的归并排序

由于CUDA不支持递归kernel，需要采用自底向上的方式：

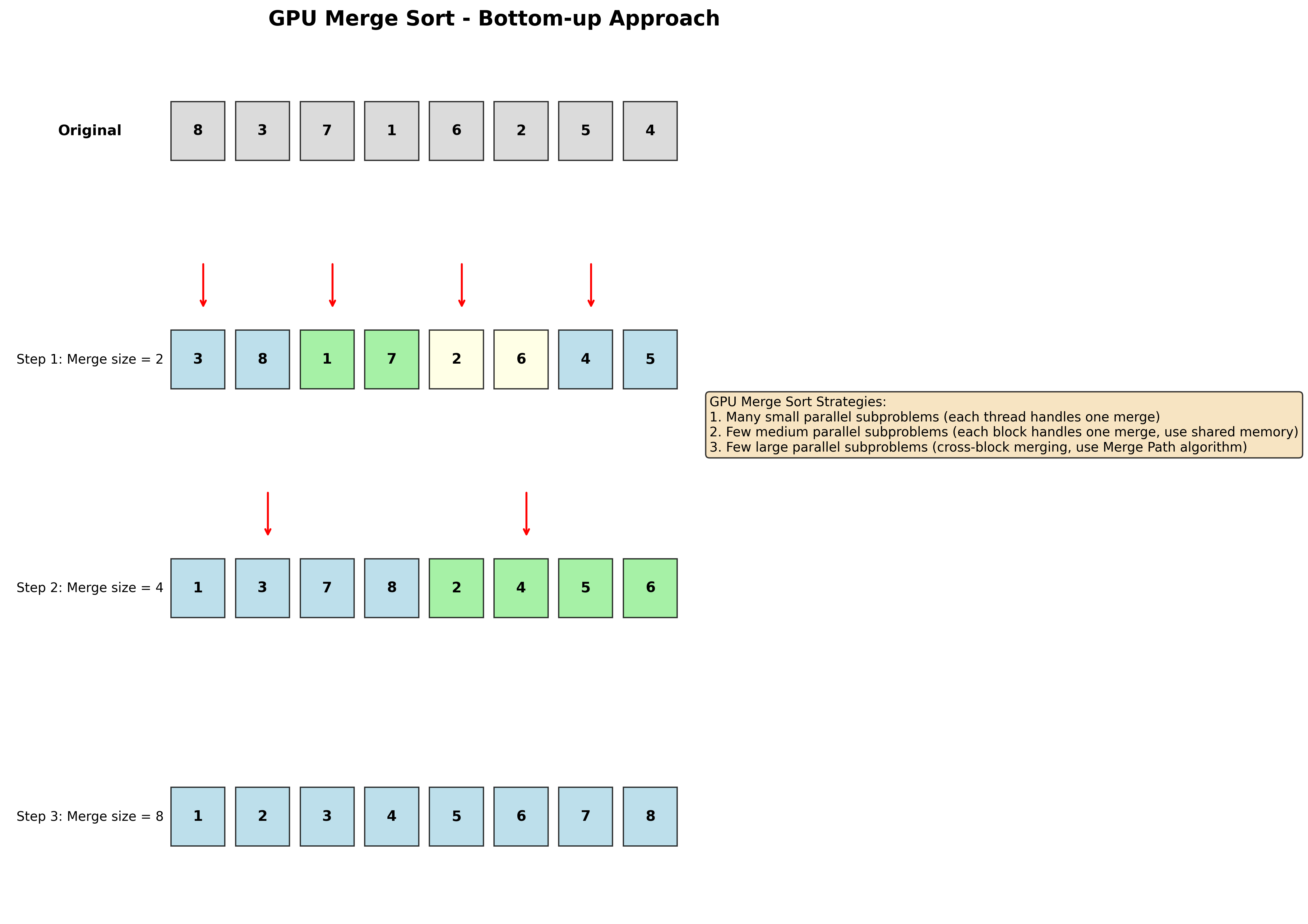
三种策略：

1. 许多小并行子问题：每个线程负责一次合并
2. 少数中等并行子问题：每个块负责一次合并，利用共享内存和二分搜索
3. 少数大并行子问题：跨块合并，使用Merge Path算法

合并操作优化

中等子问题的处理：

• 利用共享内存提高访问速度
• 使用二分搜索优化合并过程

大子问题的处理：

• 采用Merge Path算法将大问题分解为小问题
• 参考文献：”Merge Path - Parallel Merging Made Simple” (IEEE IPDPS 2012)

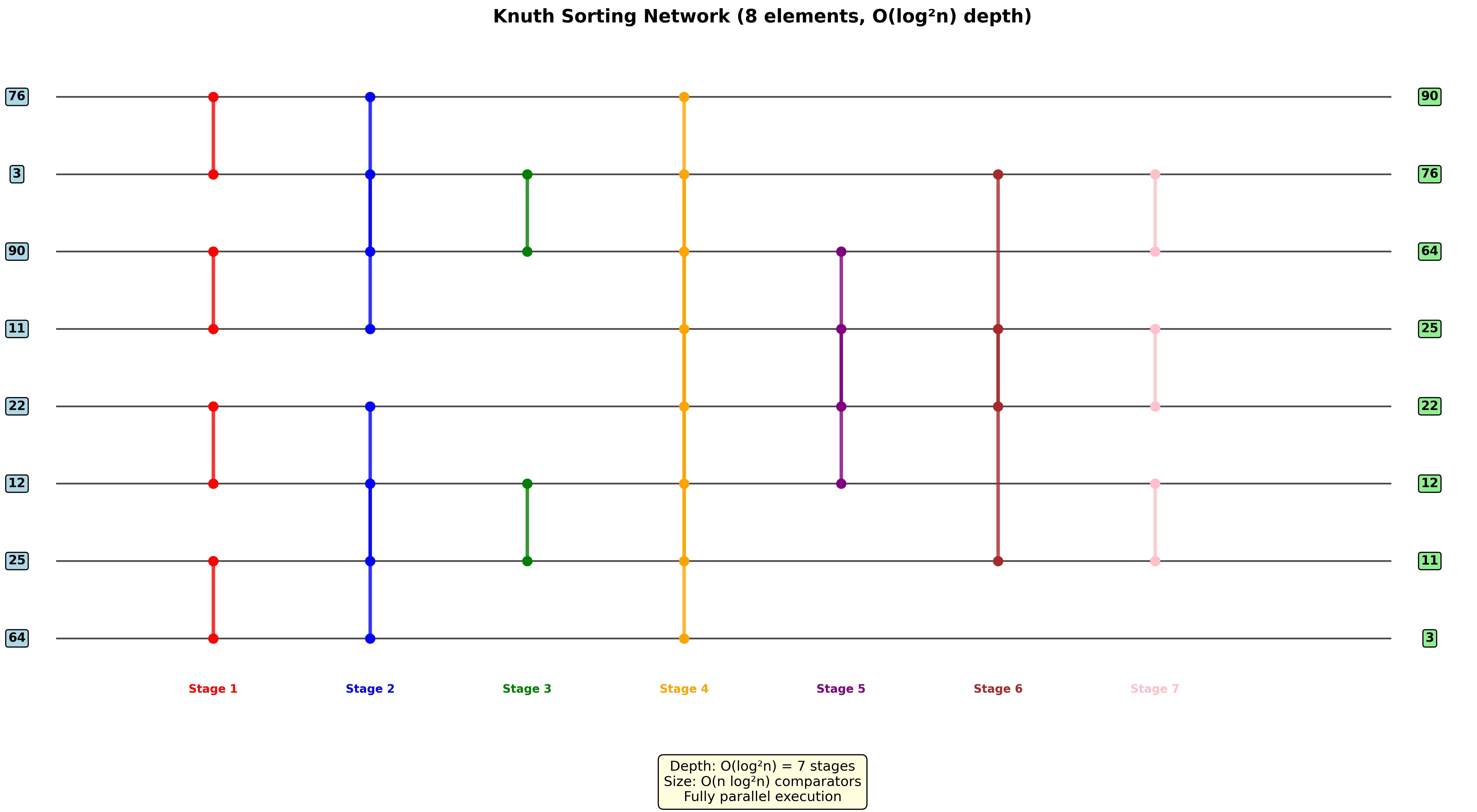
排序网络（Sorting Networks）

基本概念

排序网络由一组比较器和连接线组成：

比较器：

• 输入：x和y
• 输出：x’ = min(x,y), y’ = max(x,y)

网络深度

排序网络的运行时间与其深度成正比：

深度计算规则：

• 输入线的深度为0
• 比较器的输出深度 = max(输入深度) + 1

经典排序算法的网络表示

冒泡排序网络：

• 步复杂度：$O(N)$

插入排序网络：

• 步复杂度：$O(N)$

双调排序网络（Bitonic Sorting Network）

双调序列定义：

• 单调递增然后单调递减的序列
• 或者可以循环移位成为这样的序列

示例：

• [1, 4, 6, 8, 3, 2]
• [6, 9, 4, 2, 3, 5]
• [0, 0, 1, 1, 0, 0]

Zero-One原理

引理：如果一个比较网络能正确转换输入序列a到输出序列b，那么对于任何单调递增函数f，该网络也能正确转换f(a)到f(b)。

这意味着只需验证网络在0-1序列上的正确性。

半清理器（Half-Cleaner）

性质：如果输入是0和1的双调序列，则输出满足：

• 上半部分和下半部分都是双调的
• 至少一半是”干净的”（全0或全1）

双调排序器复杂度

递推关系：

结果：$T(n) = O(\log n)$

归并网络

将两个已排序数组合并为双调序列的技巧：

• 反转第二个序列的顺序
• 连接两个序列得到双调序列

完整排序网络

SORTER[n]递推：

总复杂度：$T(n) = O(\log^2 n)$

排序网络历史

• 1954年：P.N. Armstrong, R.J.Nelson和D.J.O’Connor首次探索排序网络
• 1960年代早期：K.E. Batcher发现第一个能在$O(\log n)$时间内合并两个n元素序列的网络
• 1983年：AKS排序网络，能在深度$O(\log n)$内使用$O(n \log n)$个比较器排序n个数

基数排序（Radix Sort）

基本思想

基数排序是按位数字排序：

错误做法：从最高有效位开始排序 正确做法：从最低有效位开始，使用辅助的稳定排序

并行优化

关键观察：可以使用之前介绍的紧缩（Compact）算法来排序二进制位。

复杂度：每位的排序复杂度为$O(\log N)$

CUDA流（Streams）

默认流（Stream ‘0’）

特点：

• 未指定流时使用Stream 0
• 默认流中的所有CUDA操作都是同步的
• GPU kernel默认与主机异步执行

// 完全同步执行
cudaMemcpy(dev1, host1, size, H2D);
kernel2<<<grid, block>>>(..., dev2, ...);
some_cpu_method(); // 可能重叠
kernel3<<<grid, block>>>(..., dev3, ...);
cudaMemcpy(host4, dev4, size, D2H);

并发性（Concurrency）

定义：同时执行多个CUDA操作的能力，超越多线程并行性。

支持的操作类型：

• CUDA Kernel执行
• cudaMemcpyAsync (Host到Device)
• cudaMemcpyAsync (Device到Host)
• CPU计算

Fermi GPU架构支持：

• 最多16个并发CUDA kernel（实际中少于4个）
• 2个cudaMemcpyAsync（必须是不同方向）
• CPU计算

性能提升示例

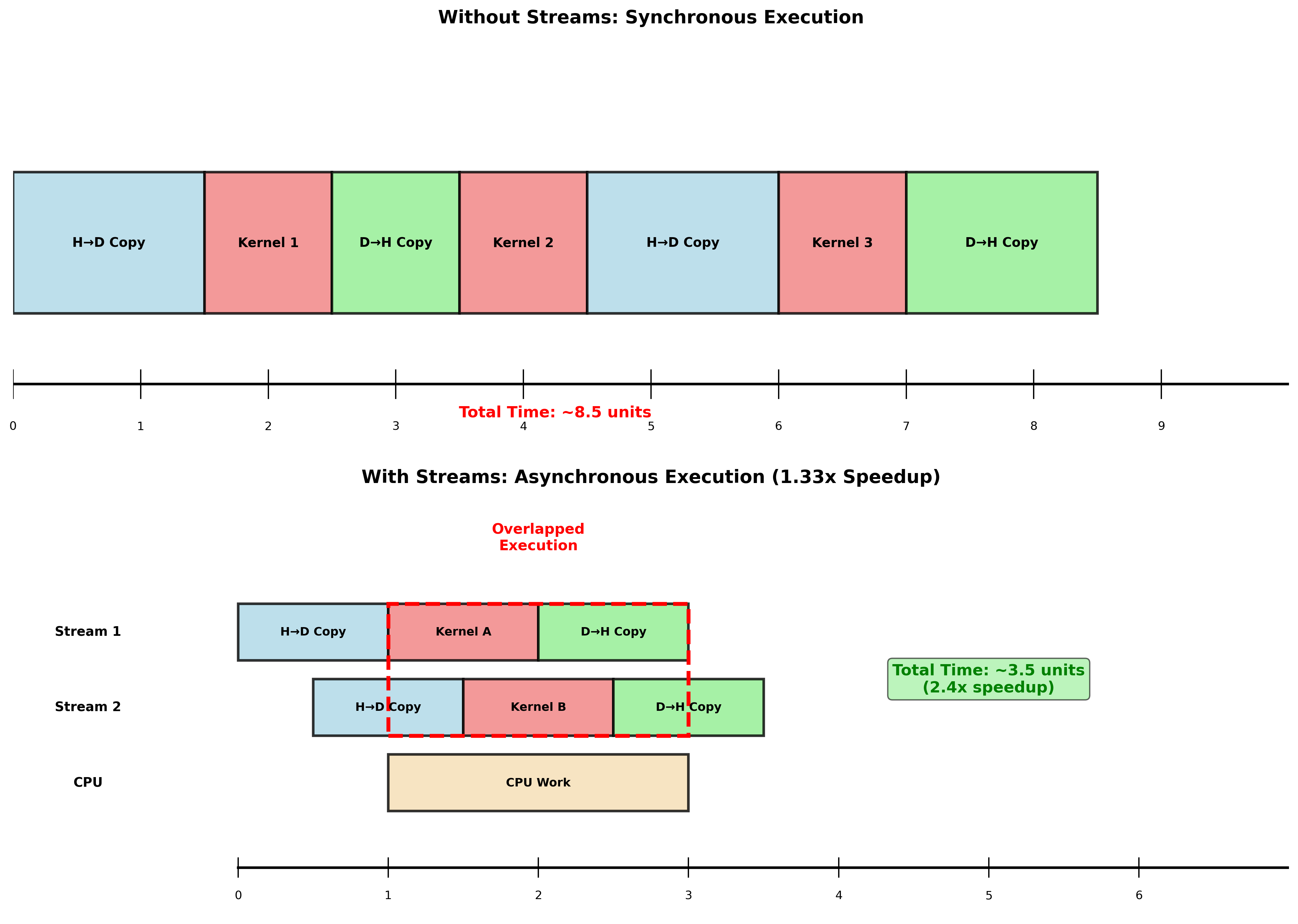
通过重叠kernel执行和内存传输，可以获得1.33倍的性能提升。

流的异步使用

cudaStream_t stream1, stream2, stream3, stream4;
cudaStreamCreate(&stream1);
cudaMalloc(&dev1, size);
cudaMallocHost(&host1, size); // 主机端需要固定内存

cudaMemcpyAsync(dev1, host1, size, H2D, stream1);
kernel2<<<grid, block, 0, stream2>>>(..., dev2, ...);
kernel3<<<grid, block, 0, stream3>>>(..., dev3, ...);
cudaMemcpyAsync(host4, dev4, size, D2H, stream4);
some_CPU_method();

重要要求：

• 完全异步/并发执行
• 并发操作使用的数据必须是独立的

固定内存（Pinned Memory）

优势：从固定（页锁定）内存的主机到GPU复制速度更快

cudaMallocHost(&host1, size); // 固定内存

PyTorch中的应用：

# DataLoader中的pin_memory参数
DataLoader(..., pin_memory=True)

显式同步

同步所有操作：

cudaDeviceSynchronize() // 阻塞主机直到所有CUDA调用完成

同步特定流：

cudaStreamSynchronize(streamid) // 阻塞直到指定流完成

使用事件同步：

cudaEventRecord(event, streamid)
cudaEventSynchronize(event)
cudaStreamWaitEvent(stream, event)
cudaEventQuery(event)

总结

核心排序算法回顾

1. 砖块排序：简单并行化，但效率不高
2. 归并排序：分治思想，在GPU上需要自底向上实现
3. 排序网络：固定比较序列，深度决定性能
4. 基数排序：利用并行紧缩算法优化位排序

性能优化原则

1. 并行度选择：最大并行度不一定是最优选择
2. 内存访问模式：合并访问比分散访问更重要
3. 流的使用：通过异步操作重叠计算和通信
4. 算法复杂度权衡：在步复杂度和工作复杂度间平衡

CUDA流的核心价值

CUDA流技术使得GPU计算能够真正实现：

• 计算与通信重叠：在执行kernel的同时进行内存传输
• 多任务并发：同时处理多个独立的计算任务
• 资源利用率最大化：充分利用GPU的并行执行单元

这些技术为构建高性能GPU应用程序提供了重要基础，特别是在深度学习等需要处理大规模数据的场景中。