人工智能中的编程 - 第4章: 并行算法(Parallel Algorithms)
上节课回顾
GPU内存
- 内存管理;Tensor
- Local / Shared / Global内存层次结构
GPU硬件
- 并行化线程和块
- SIMT:单指令多线程
同步
- 屏障(Barrier)
- 原子操作(Atomic operations)
通信模式
- Map, Gather, Scatter, Stencil, Transpose
主要内容
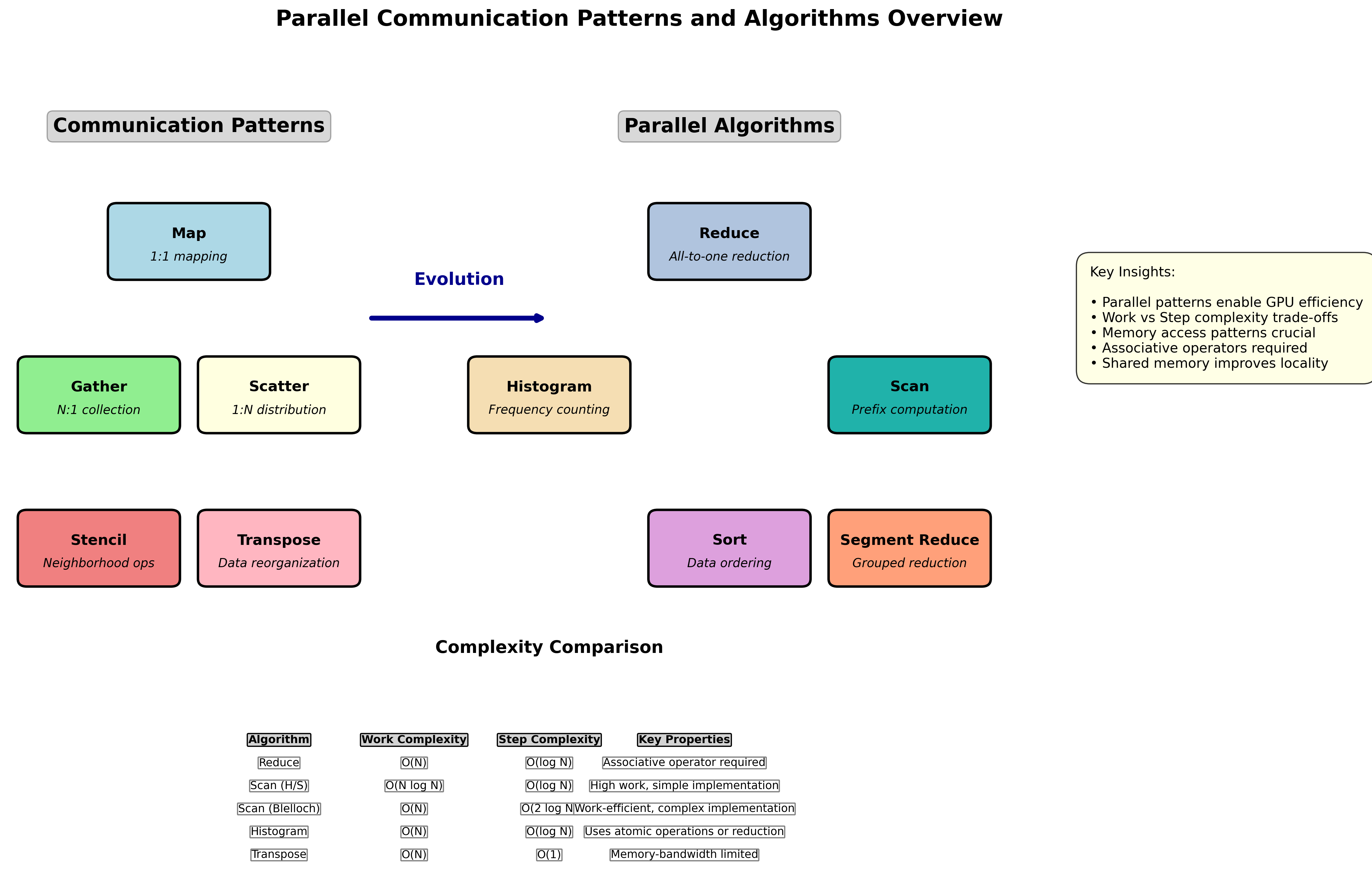
从通信模式扩展到并行算法:
| 通信模式 | 并行算法 |
|---|---|
| Map, Gather, Scatter | Reduce, Scan, Histogram |
| Stencil, Transpose | Sort, Segment Reduce |
并行归约(Parallel Reduction)
基本概念
计算 $s = \sum_i x_i$ 的并行版本是最重要的并行算法模式之一。
核心思想:利用运算的结合律,将线性的串行计算转换为对数深度的并行计算。
应用场景:
- 张量统计计算:
torch.mean(input),torch.sum(input),torch.max(input) - 神经网络训练中的损失函数计算:交叉熵损失、均方误差等
- Batch Normalization:
- 计算批次均值:$\mu = \frac{1}{N}\sum_{i=1}^{N} x_i$
- 计算批次方差:$\sigma^2 = \frac{1}{N}\sum_{i=1}^{N} (x_i - \mu)^2$
- 标准化特征:$\hat{x}_i = \frac{x_i-\mu}{\sqrt{\sigma^2 + \epsilon}}$
- Group Normalization:在通道组内进行类似的统计计算
- 向量范数计算:$|x|2 = \sqrt{\sum{i=1}^{N} x_i^2}$
复杂度分析
CPU串行实现:
float sum = 0;
for (int i = 0; i < N; i++) {
sum += h_in[i];
}
- 工作复杂度:$O(N)$
- 步复杂度:$O(N)$ - 串行,在GPU上运行缓慢
GPU并行实现:
- 加法运算满足结合律
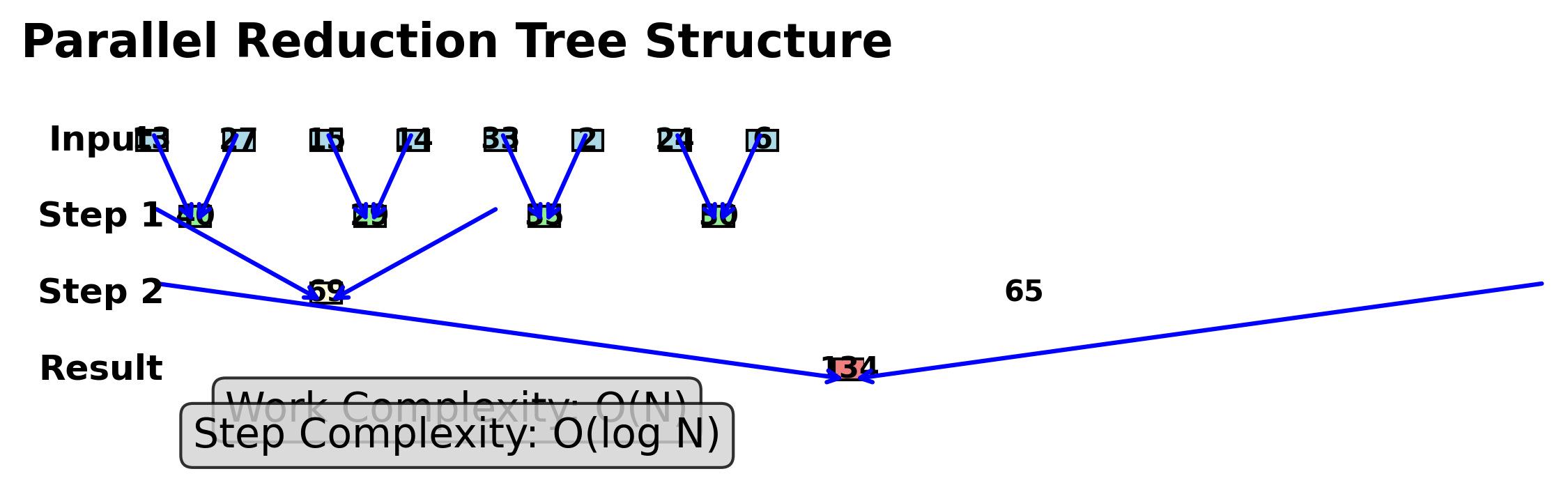
- 使用”浅层树”结构进行并行加法
- 工作复杂度:$O(N)$
- 步复杂度:$O(\log N)$
寻址策略详解
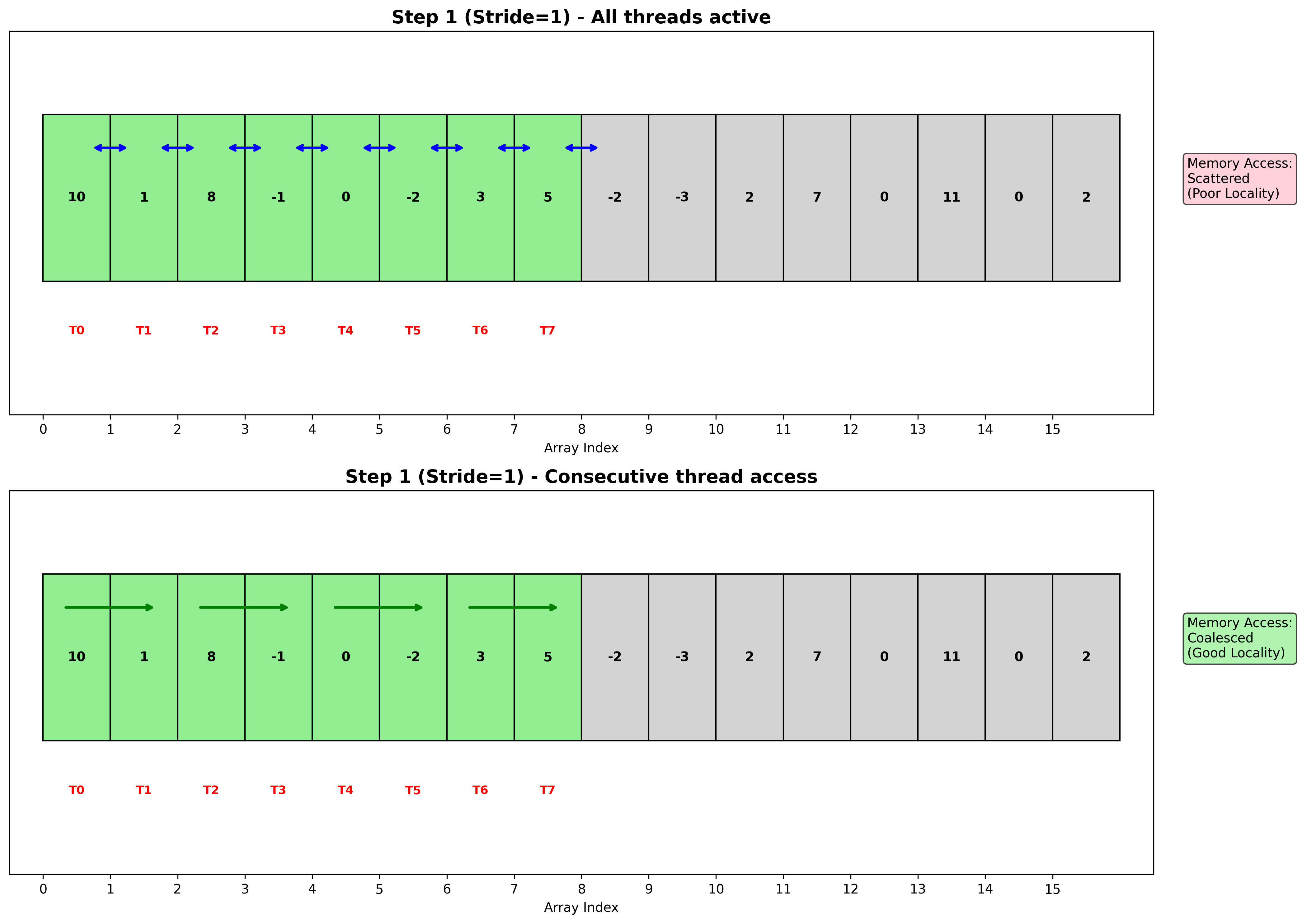
GPU并行归约中的寻址模式对性能至关重要,主要有两种策略:
1. 交错寻址 (Interleaved Addressing)
特点:
- 线程访问的内存地址跳跃性很大
- 线程间距随步骤增加:1, 2, 4, 8, …
- 容易造成内存访问不合并
问题:
- 内存访问模式不规律,影响缓存效率
- Warp内线程访问的地址分散,无法利用合并访问
2. 顺序寻址 (Sequential Addressing)
特点:
- 活跃线程总是连续的:0, 1, 2, 3, …
- 内存访问地址连续,利于合并访问
- 更好的数据局部性
优势:
- 更好的数据局部性:连续内存访问提高缓存命中率
- 跨块无冲突访问:不同块之间的内存访问模式不会冲突
- 合并内存访问:Warp内线程访问连续地址,提高带宽利用率
使用全局内存的并行归约
__global__ void reduce_global(float *d_out, float *d_in, int N) {
int tid = threadIdx.x;
int idx = threadIdx.x + blockDim.x * blockIdx.x;
for (int s = blockDim.x / 2; s > 0; s >>= 1) {
if (tid < s && idx < N && idx + s < N) {
d_in[idx] += d_in[idx + s];
}
__syncthreads(); // 确保同一阶段的所有加法完成
}
// 只有线程0将此块的结果写入全局内存
if (tid == 0) { d_out[blockIdx.x] = d_in[idx]; }
}
问题:
- 合并的全局内存访问?
- 能否使用共享内存提升速度?
使用共享内存的并行归约
__global__ void reduce_shared(float *d_out, const float *d_in, int N) {
int tid = threadIdx.x;
int idx = threadIdx.x + blockDim.x * blockIdx.x;
// 在kernel调用时使用 <<<b, t, shmem>>> 动态分配
extern __shared__ float shared[];
shared[tid] = idx < N ? d_in[idx] : 0;
__syncthreads(); // 确保整个块已加载!
for (int s = blockDim.x / 2; s > 0; s >>= 1) {
if (tid < s) {
shared[tid] += shared[tid + s];
}
__syncthreads(); // 确保同一阶段的所有加法完成!
}
// 只有线程0将此块的结果写入全局内存
if (tid == 0) { d_out[blockIdx.x] = shared[0]; }
}
优势:使用共享内存减少全局内存访问
两级归约实现
void reduce(float *d_out, float *d_in, int N) {
float *d_tmp;
cudaMalloc((void **)&d_tmp, CudaGetBlocks(N) * sizeof(float));
int num = N;
float *ptr_in = d_in;
float *ptr_out = d_tmp;
int kShared = kThreadsNum * sizeof(float);
while (num > 1) {
int blocks = CudaGetBlocks(num);
// 动态分配共享内存 <<<b, t, shmem>>>
reduce_shared<<<blocks, kThreadsNum, kShared>>>(ptr_out, ptr_in, num);
num = blocks;
std::swap(ptr_in, ptr_out);
}
cudaMemcpy(d_out, ptr_in, sizeof(float), cudaMemcpyDeviceToDevice);
cudaFree(d_tmp);
}
直方图:归约的应用
CPU实现:
for (int i = 0; i < N; i++) {
// 计算bin索引
int bin = h_in[idx] % kBinCount;
h_bins[bin]++;
}
朴素GPU实现:
__global__ void naive_histo(int *d_bins, const int *d_in,
const int kBinCount) {
int idx = threadIdx.x + blockDim.x * blockIdx.x;
int bin = d_in[idx] % kBinCount;
atomicAdd(&(d_bins[bin]), 1); // "读-修改-写"操作
}
问题:atomicAdd虽然保证正确性,但速度较慢
优化策略 - 分层直方图:
考虑一个具体的例子:
- 数据规模:$512^2 = 262,144$ 个元素
- 直方图桶数:10个桶
- GPU配置:512个块,每块512个线程
分层实现步骤:
- 第一阶段:每个线程块维护局部直方图
- 每个块处理512个元素
- 使用共享内存存储局部直方图(10个桶)
- 块内使用原子操作更新局部直方图
- 第二阶段:合并所有局部直方图
- 512个局部直方图需要归约为1个全局直方图
- 对每个桶使用并行归约算法
- 最终得到完整的全局直方图
性能优势:
- 减少全局原子操作的冲突
- 提高内存访问的局部性
- 利用共享内存的高带宽
并行扫描(Parallel Scan)
基本概念详解
并行扫描(Prefix Sum) 是另一个基础的并行算法模式。
定义:
- 包含扫描:$y_i = \bigoplus_{j=0}^{i} x_j$,其中$\bigoplus$是结合运算符
- 排除扫描:$y_i = \bigoplus_{j=0}^{i-1} x_j$
PyTorch中的torch.cumsum:
- 输入:(1, 2, 3, 4)
- 包含扫描:(1, 3, 6, 10) — 每个位置包含到当前位置的累积
- 排除扫描:(0, 1, 3, 6) — 每个位置不包含当前元素
算法重要性:
- 在串行编程中看似简单,但在并行计算中是核心构建块
- 可以解决许多传统上难以并行化的问题
- 是许多复杂并行算法的基础
典型应用场景:
- 并行紧缩 (Parallel Compaction):
import torch
a = torch.rand(5, 2)
b = torch.tensor([1,0,0,1,0], dtype=bool)
c = a[b] # 使用布尔索引进行紧缩
- 并行排序算法:基数排序、快速排序的分区操作
- 图算法:广度优先搜索、连通分量计算
- 字符串算法:并行字符串匹配、后缀数组构建
- 几何算法:凸包计算、最近点对问题
CPU实现
float sum = 0;
for (int i = 0; i < N; i++) {
sum += array[i];
out[i] = sum; // 比归约多一行代码
}
- 工作复杂度:$O(N)$
- 步复杂度:$O(N)$ - 串行,GPU上运行缓慢
GPU并行实现
给定并行归约算法,$s_k$是对$x_0$到$x_k$的并行归约:
- 步复杂度:$O(\log N)$
- 朴素实现的工作复杂度:$O(N^2)$
- 优化后的工作复杂度:$O(N \log N)$
Hillis/Steele包含扫描
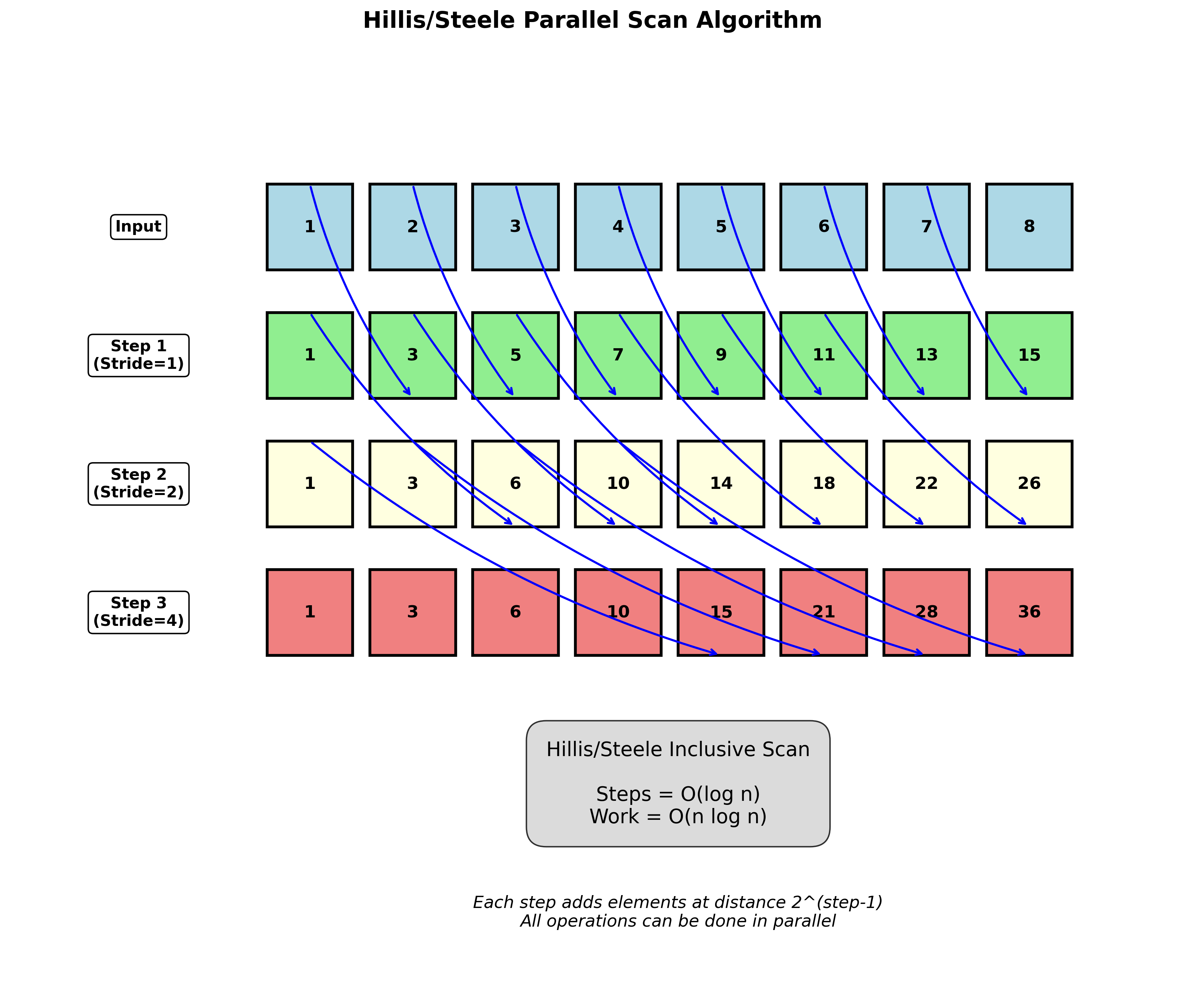
算法步骤:
- 步骤1:添加直接邻居 n = 1
- 步骤2:添加距离为2的邻居 n = 2
- 步骤3:添加距离为4的邻居 n = 4
- 一般地:n = $2^{step}$
复杂度:
- 步数:$O(\log n)$
- 工作量:$O(n \log n)$ (矩形区域的维度)
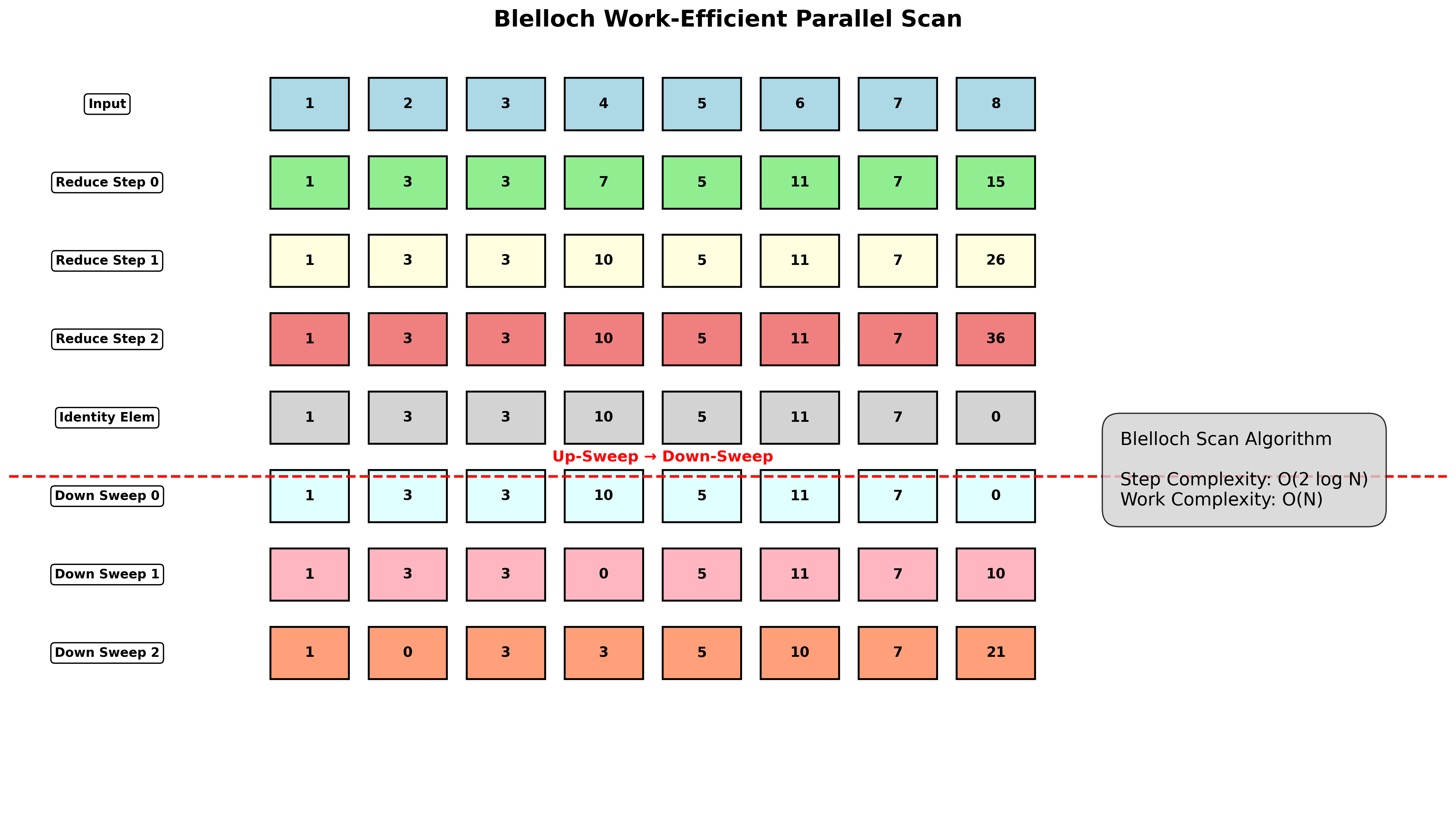
Blelloch扫描(工作高效算法)
更高效的$O(N)$工作量实现:
两阶段算法:
- 上扫描阶段:类似归约操作
- 下扫描阶段:分发部分和
复杂度:
- 步复杂度:$O(2\log N)$
- 工作复杂度:$O(N)$
并行紧缩
使用扫描实现数组紧缩:
- 运行判定条件
- 创建数组:True = 1,False = 0
- 运行排除扫描:输出为剩余输入的地址
- 将输入复制到输出数组
示例:
- 输入:[1, 2, 3, 4, 5, 6, 7, 8]
- 判定:[T, F, T, F, T, F, T, F]
- 扫描:[1, -, 3, -, 5, -, 7, -]
- 输出:[1, 3, 5, 7]

分段扫描
对输入数组的任意连续分区执行扫描:
示例:
- 输入:[[1, 2], [6, 7, 1], [1, 2, 3, 4]]
- 排除扫描:[[0,1], [0, 6, 13], [0,1,3,6]]
头标志表示法:
- Flag = [1, 0, 1, 0, 0, 1, 0, 0, 0]
- Data = [1, 2, 6, 7, 1, 1, 2, 3, 4]
复杂度:分段扫描的步复杂度也是$O(\log N)$
矩阵转置(Transpose)
CPU实现
void transpose(float in[], float out[]) {
for (int j = 0; j < N; j++) {
for (int i = 0; i < N; i++) {
// out(j,i) = in(i,j)
out[i * N + j] = in[j * N + i];
}
}
}
GPU实现策略
策略2:每行一个线程
__global__ void transpose_per_row(float in[], float out[]) {
int i = threadIdx.x;
for (int j = 0; j < N; j++) {
// out(j,i) = in(i,j)
out[i * N + j] = in[j * N + i];
}
}
策略3:每元素一个线程(最大并行度)
__global__ void transpose_per_element(float in[], float out[]) {
int i = threadIdx.x;
int j = blockIdx.x;
// out(j,i) = in(i,j)
out[i * N + j] = in[j * N + i];
}
问题:最大并行度并不总是最佳选择
内存访问优化
大多数GPU程序是内存受限的:
- 最后的实现:合并读取,分散写入
- 目标:合并读取,合并写入
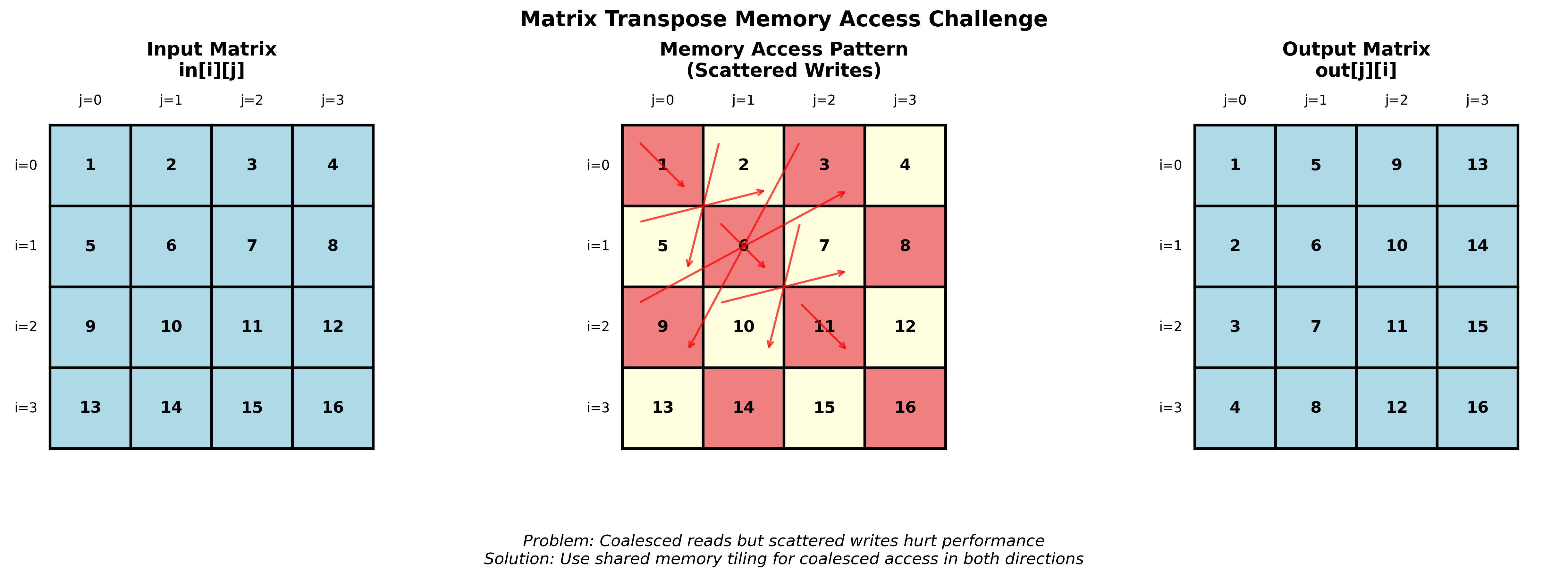
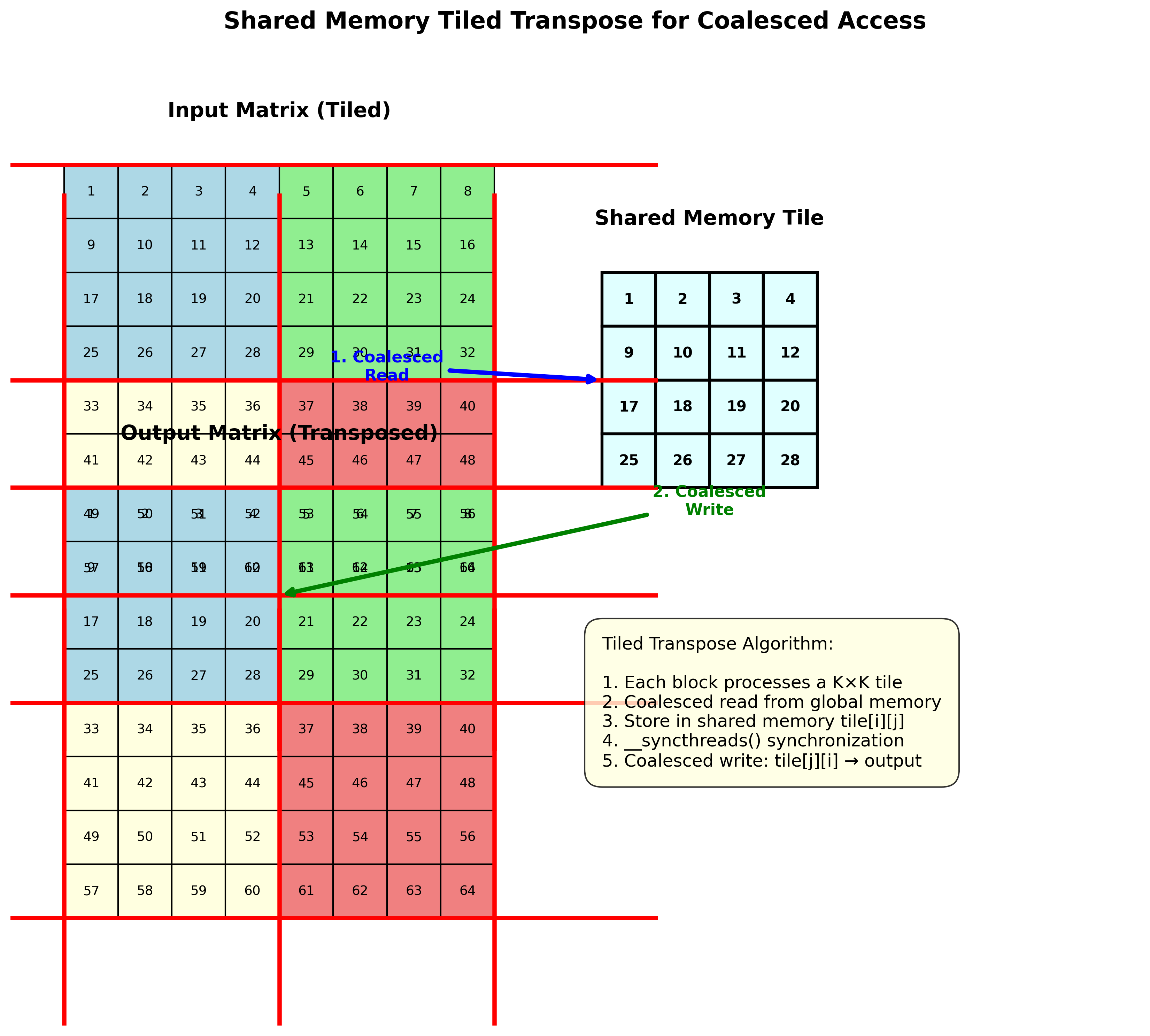
分块转置实现
__global__ void transpose_tiled(float in[], float out[]) {
// (i,j) 是瓦片角点
int i = blockIdx.x * K, j = blockIdx.y * K;
int x = threadIdx.x, y = threadIdx.y;
// 从全局内存合并读取
__shared__ float tile[K][K];
tile[x][y] = in[(j + y) * N + (i + x)];
__syncthreads();
// 向全局内存合并写入
out[(i + y) * N + (j + x)] = tile[y][x];
}
// 启动kernel
dim3 blocks(N / K, N / K);
dim3 threads(K, K);
transpose_tiled<<<blocks, threads>>>(d_in, d_out);
算法总结
并行归约总结
- 使用浅层树结构实现并行归约
- 工作复杂度:$O(N)$;步复杂度:$O(\log N)$
- 要求运算符为二元且满足结合律:SUM, MULTIPLY, MIN, MAX, AND, OR
- 利用数据局部性和共享内存提升效率
并行扫描总结
- 也称为前缀和、累积和
- 包含扫描和排除扫描
- 工作复杂度:$O(N)$/$O(N \log N)$;步复杂度:$O(\log N)$
- 要求运算符为二元且满足结合律:SUM, MULTIPLY, MIN, MAX, AND, OR
- 可用于解决许多难以并行化的问题,如并行紧缩
关键原则与设计考虑
算法选择原则:
-
运算符要求:所有并行归约和扫描算法都要求运算符为二元且满足结合律
- 满足条件:+, ×, min, max, ∧, ∨
- 不满足条件:- (减法), ÷ (除法)
-
复杂度权衡:
- 工作复杂度:总计算量,影响算法效率
- 步复杂度:并行深度,影响执行时间
- Hillis/Steele: 简单实现,但工作量大 $O(N \log N)$
- Blelloch: 复杂实现,但工作高效 $O(N)$
-
内存访问模式:
- 合并访问比最大并行度更重要
- 利用共享内存提高数据局部性
- 避免分散的内存访问模式
-
实际应用考虑:
- 并行直方图:图像处理、数据分析中的频率统计
- 并行紧缩:数据过滤、稀疏矩阵操作
- 矩阵转置:线性代数库、深度学习框架的核心操作
编译和执行
开发环境设置:
- 安装Visual Studio (Windows) / gcc (Linux)
- 安装CUDA Toolkit:https://developer.nvidia.com/cuda-downloads
- 设置环境变量
- 测试编译环境:
nvcc --version
编译命令:
nvcc -o relu relu.cu
总结与展望
核心概念回顾
本讲介绍了GPU并行算法的核心模式:
- 并行归约:从$O(N)$步复杂度的串行算法到$O(\log N)$步复杂度的并行算法
- 并行扫描:看似简单的前缀和操作,实际上是解决复杂并行问题的万能工具
- 内存优化:通过合理的内存访问模式和共享内存使用提升性能
在深度学习中的应用
这些并行算法构成了现代深度学习框架的基础:
- Batch Normalization:使用并行归约计算批次统计信息
- 注意力机制:Softmax操作需要归约(求和)和扫描(前缀和)
- 梯度聚合:分布式训练中的梯度归约操作
- 动态图构建:使用并行紧缩过滤活跃的计算节点
- 矩阵运算:GEMM操作中的数据重排需要高效的转置
性能优化原则
通过本讲学习,我们理解了GPU编程的核心原则:
- 算法设计:选择适合并行的算法模式
- 内存管理:优化内存访问模式,减少带宽瓶颈
- 同步开销:在正确性和性能之间找到平衡
理解这些基础算法模式,对设计高效的GPU程序和深度学习系统至关重要。
Enjoy Reading This Article?
Here are some more articles you might like to read next: